1.2.2 الاوضاع النسبية لمستقيمين

ليكن (D) و (D') مستقيمين من الفضاء.
توجد ثلاث وضعيات.
1) (D) و (D') متقاطعان.

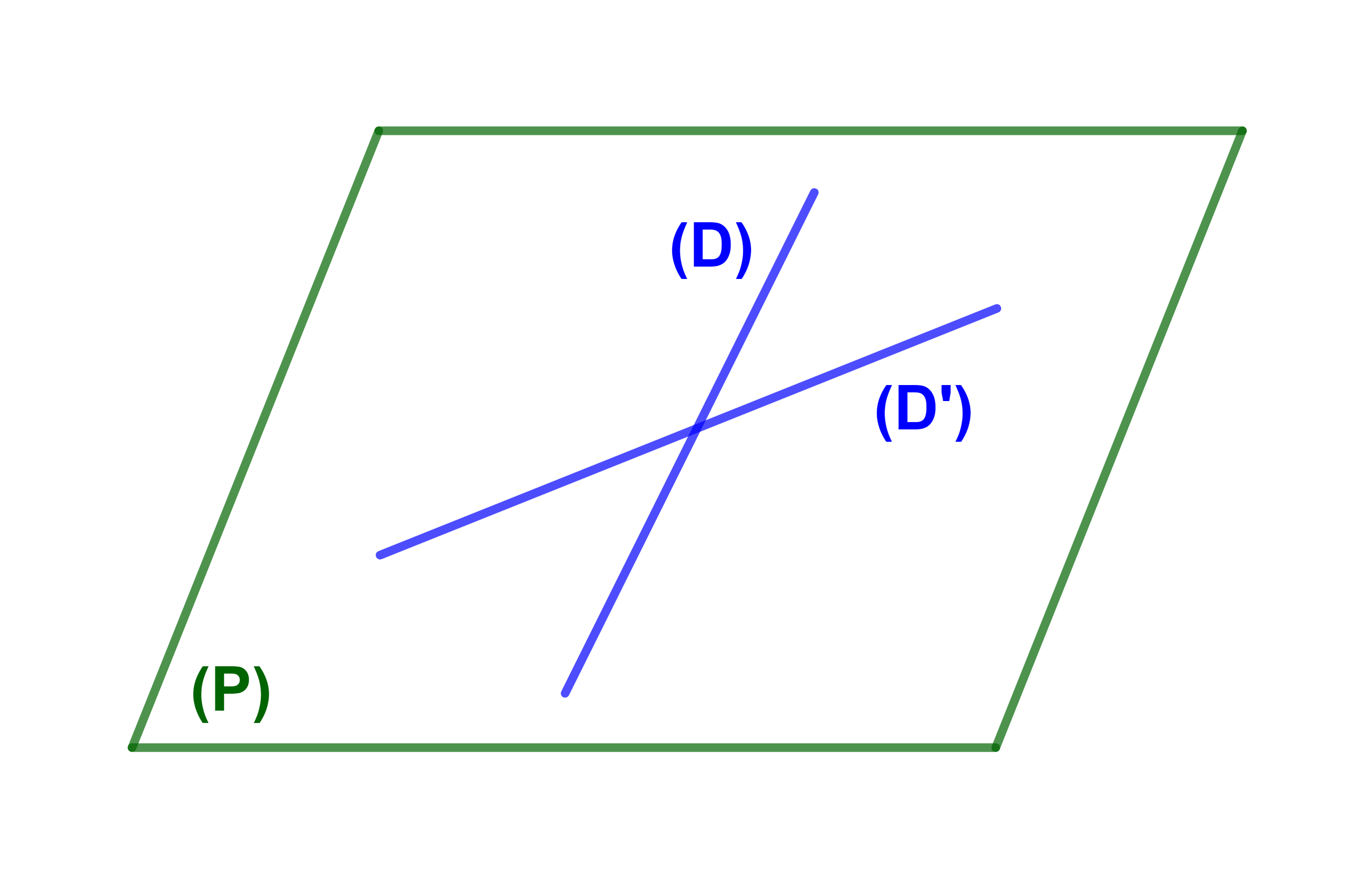
(D) و (D') يوجدان في نفس المستوى اذن مستوائيان.
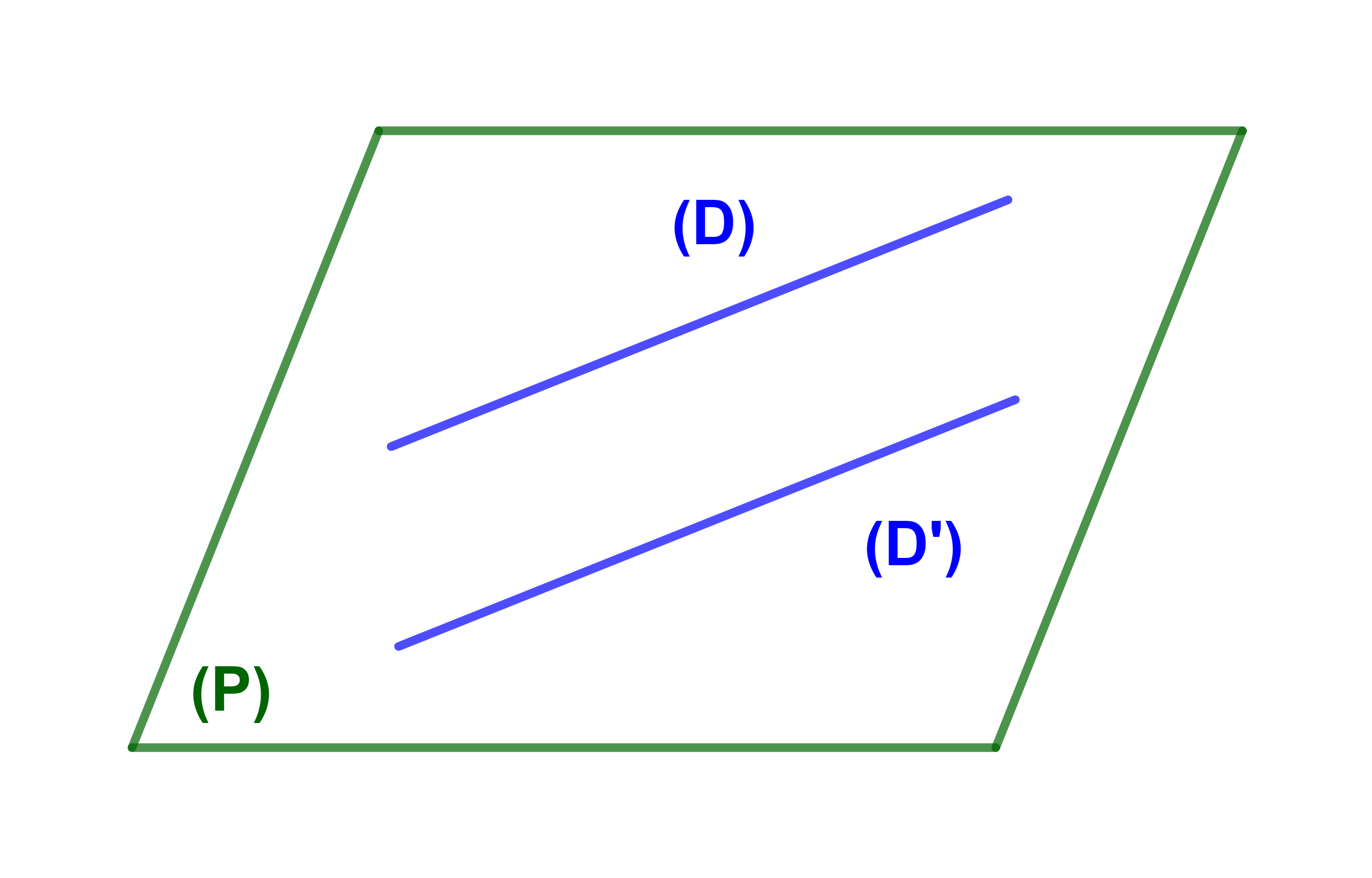
2) (D) و (D') منفصلان ومستوائيان
نقول انهما متوازيان ونكتب (D)||(D').

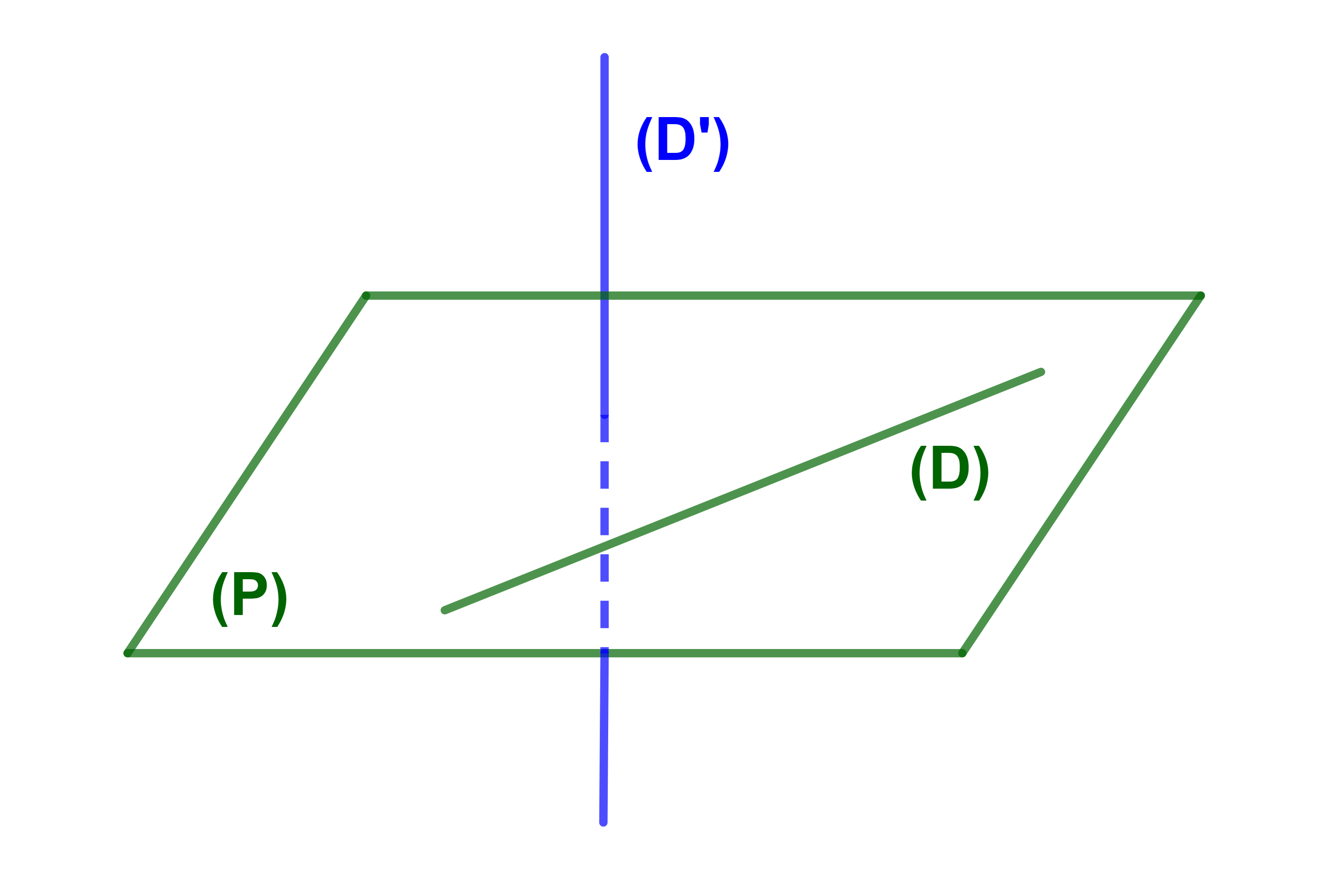
3) (D) و (D') منفصلان وغير مستوائيان
(D)∩(D')=∅.

أمثلة

ليكن (ABCDEFGH) مكعبا.

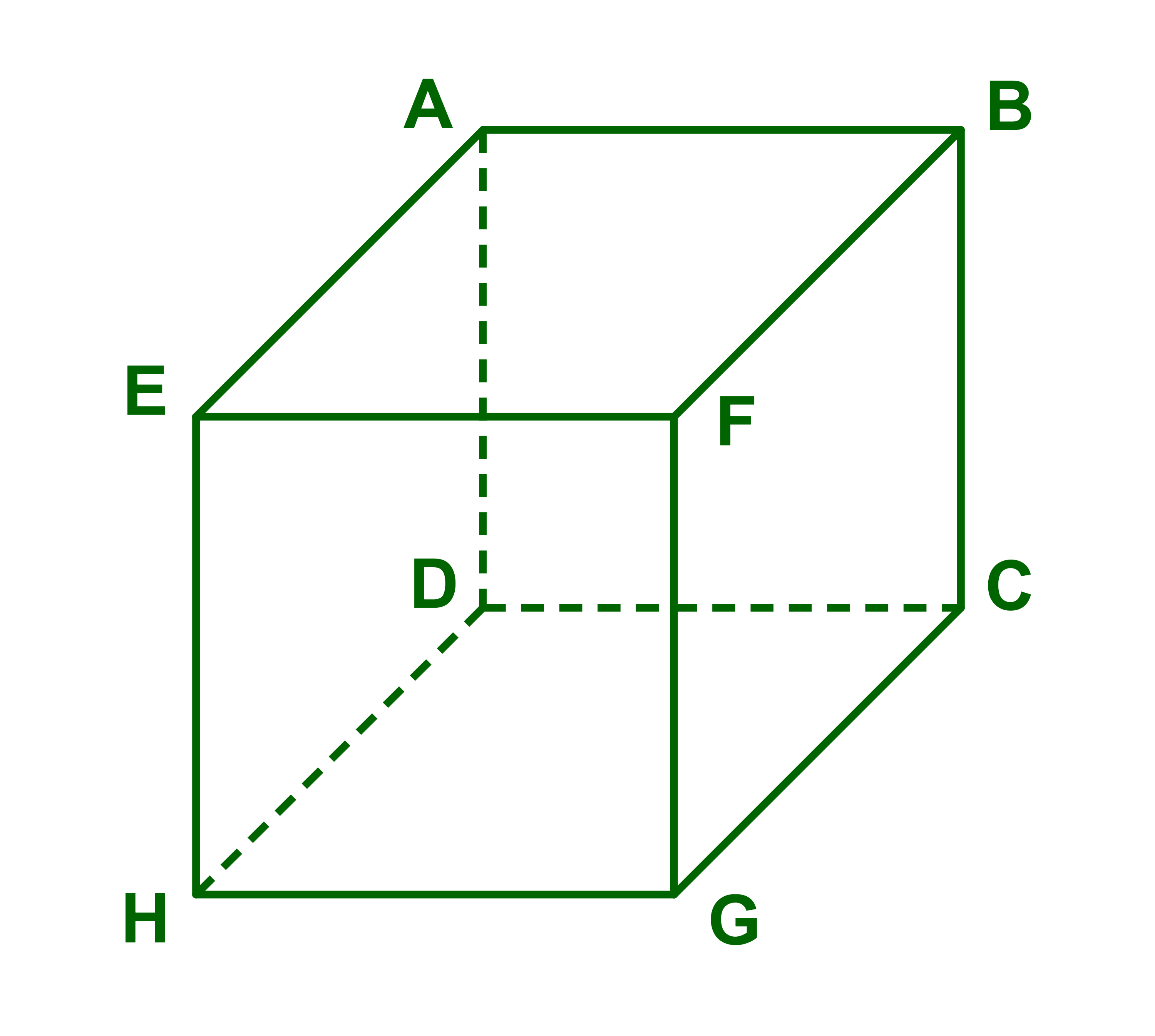
1) (AD) و (EH) مستوائيان ومنفصلان اذن متوازيان.
2) (HG) و (AE) منفصلان وغير مستوائيان اذن غير متوازيان.
3) (FH) و (EG) متقاطعان.
(FH)∩(EG)={I} بحيث I مركز المربع EFGH.

1.2.3 الاوضاع النسبية لمستويين

ليكن P و Q مستويين.
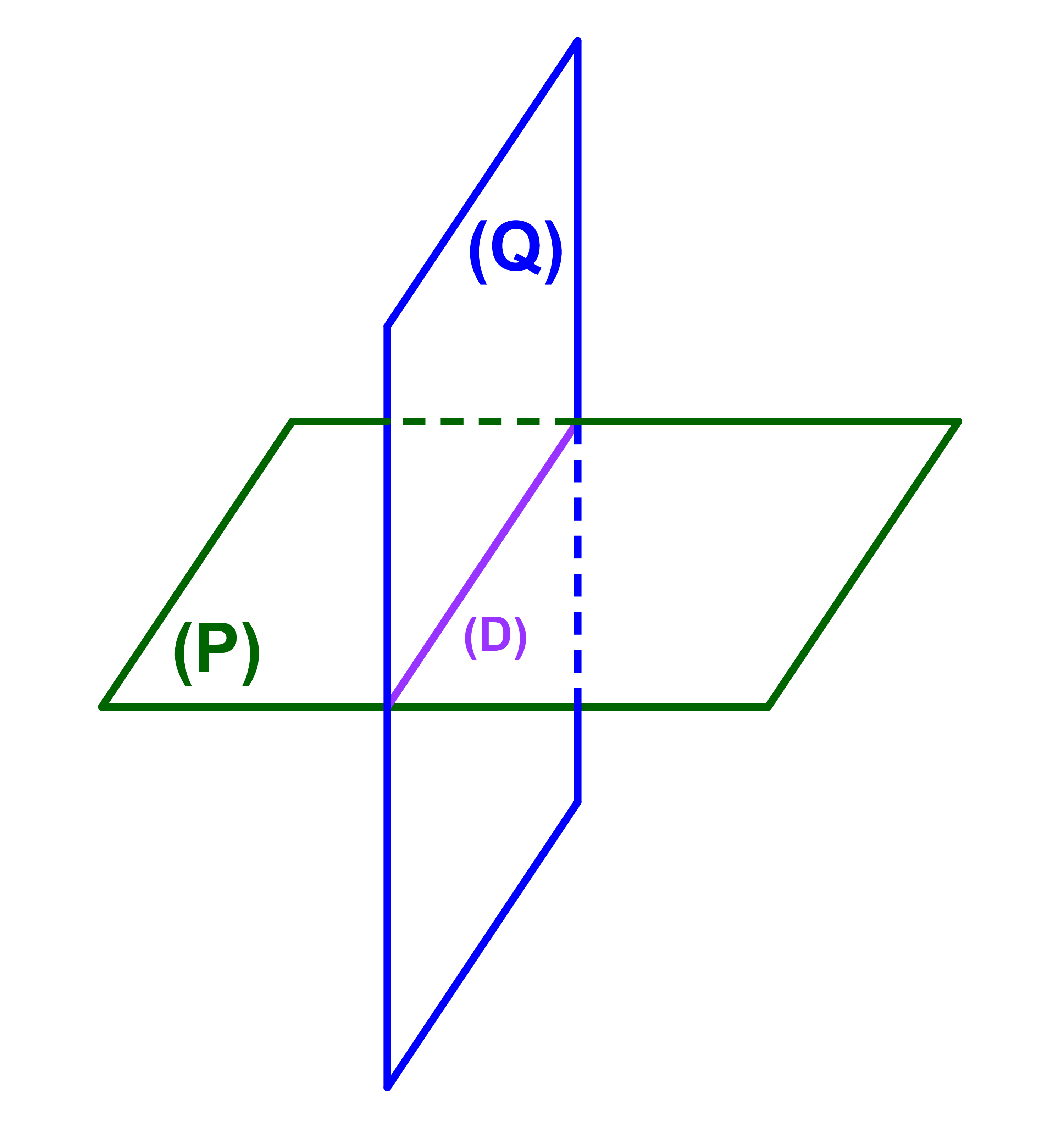
1) P و Q متقاطعان اي P⋂Q=(D).

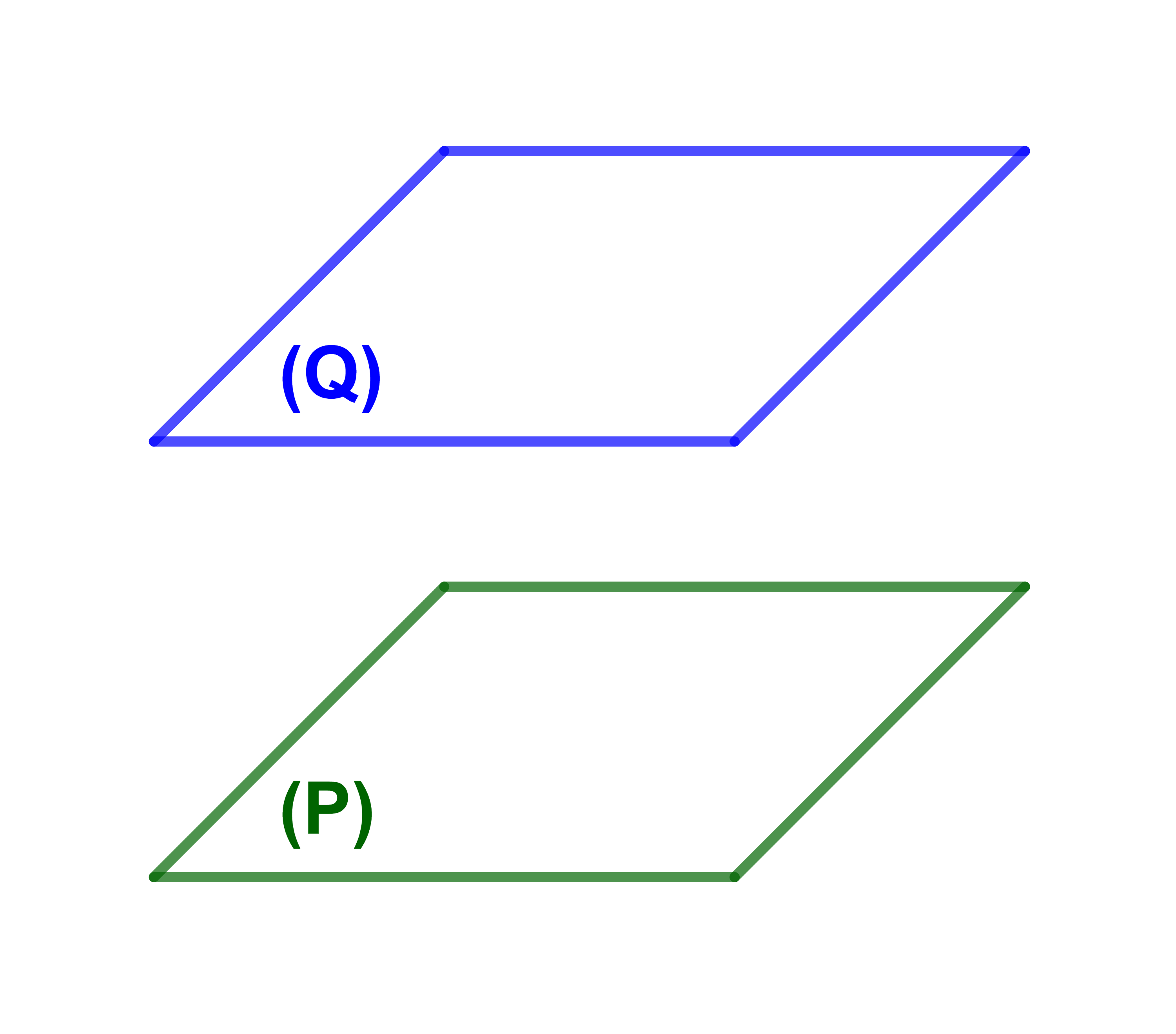
2) P و Q منفصلان اي P⋂(P')=∅.

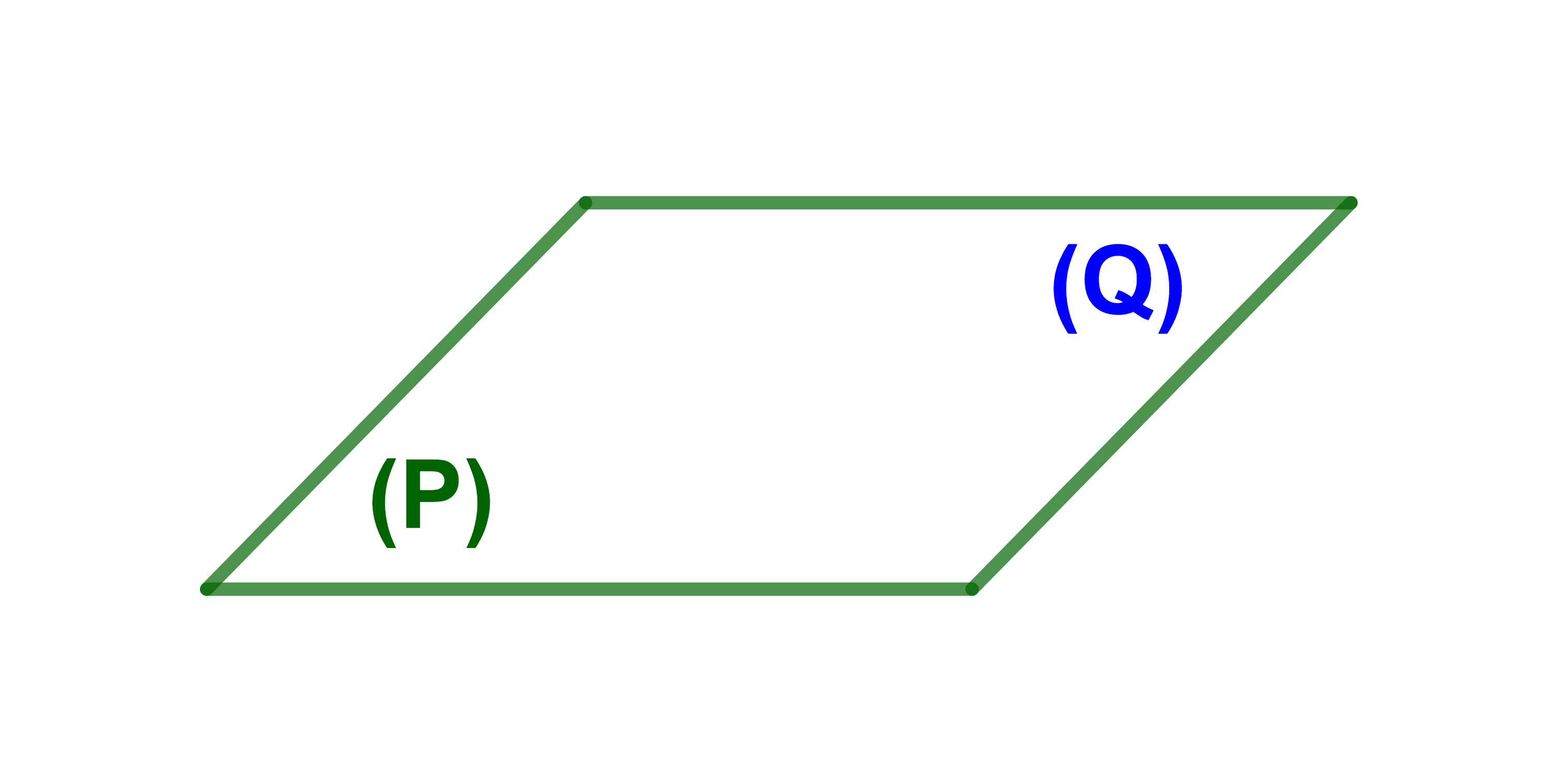
3) P=Q اذن متوازيان

أمثلة ليكن (ABCDEFGH) مكعبا.
1) المستويان (ADH) و (BFG) منفصلان والا فانهما متقاطعان وهذا يتناقض مع كون (ABCDEFGH) مربعا.
2) المستويان (ADH) و (DCG) يتقاطعان وفق المستقيم (DH).