5- حلول مبيانية لمعادلات ومتراجحات

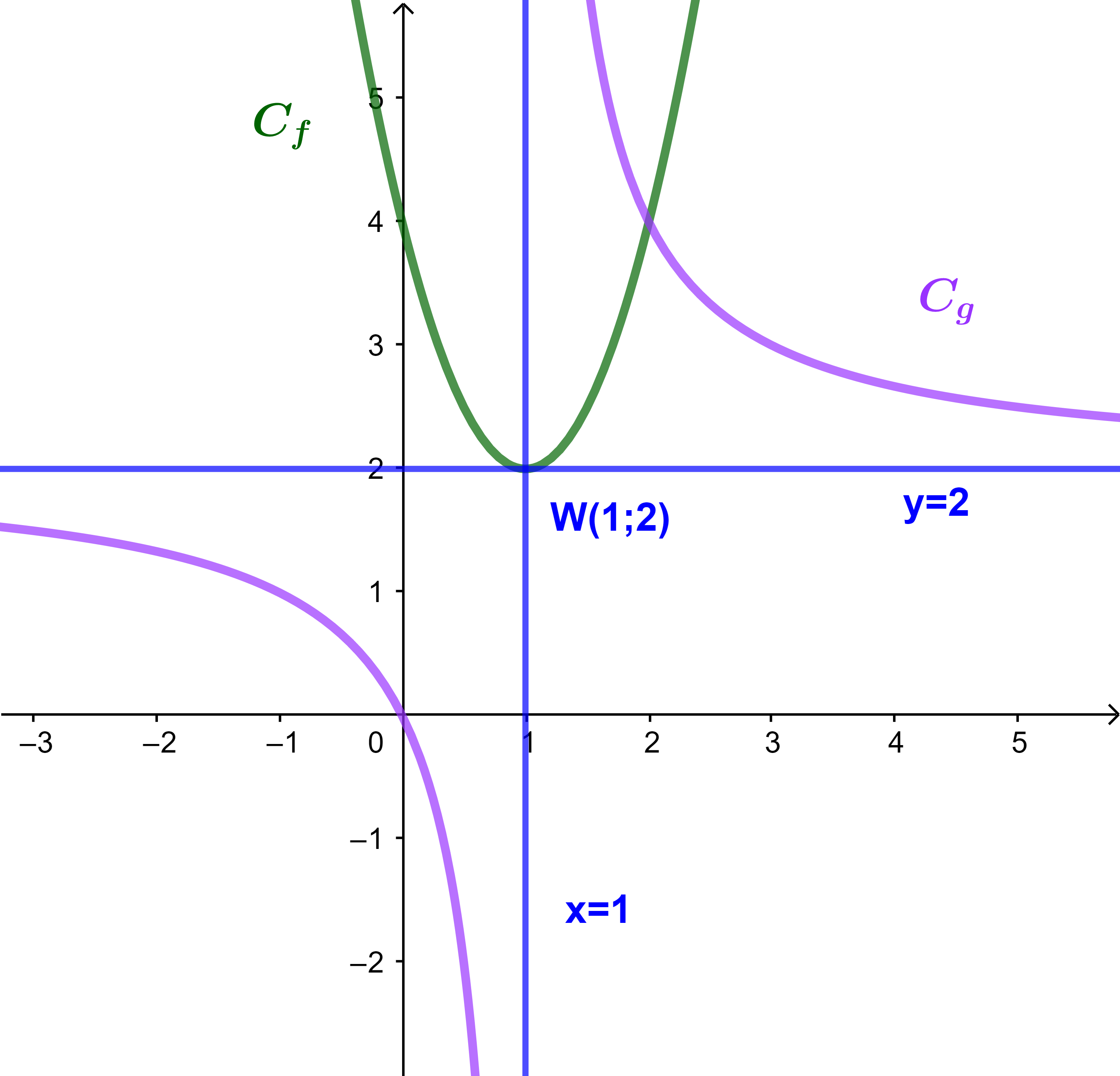
تمرين 1 tp

لتكن f و g دالتين عدديتين معرفتين كما يلي
f(x)=-2x²+4x+1 و g(x)=x²-4x+5
و (C_f) et (C_g) المنحنيين الممثلين لهما على التوالي في معلم متعامد ممنظم (O;i^→;j^→).
1) (a) بين أن لكل x∈IR
f(x)=-2(x-1)²+3.

(b) استنتج قيمة قصوى للدالة f.
2) باستعمال المبيان المرفق
(a) حل مبيانيا المعادلة f(x)=g(x).
(b) حل مبيانيا المتراجحة f(x)≥g(x).

تمرين 2 tp

لتكن f دالة عددية لمتغير حقيقي x ومعرفة بما يلي
f(x)=x²-2x-1. و (C) المنحتى الممثل لها في معلم متعامد ممنظم (O;i^→;j^→).
1) بين أن لكل x∈IR
لدينا f(x)=(x-1)²-2.
2) احسب f(1) وبين أن
لكل x∈IR لدينا f(x)-f(1)≥0.

3) استنتج مطرافا للدالة f.
4) (a) احسب f(-1) و f(2) و f(3).
(b) انشئ المنحنى (C) واستنتج تغيرات f.
(c) حل المعادلة f(x)=m حسب قيم m.

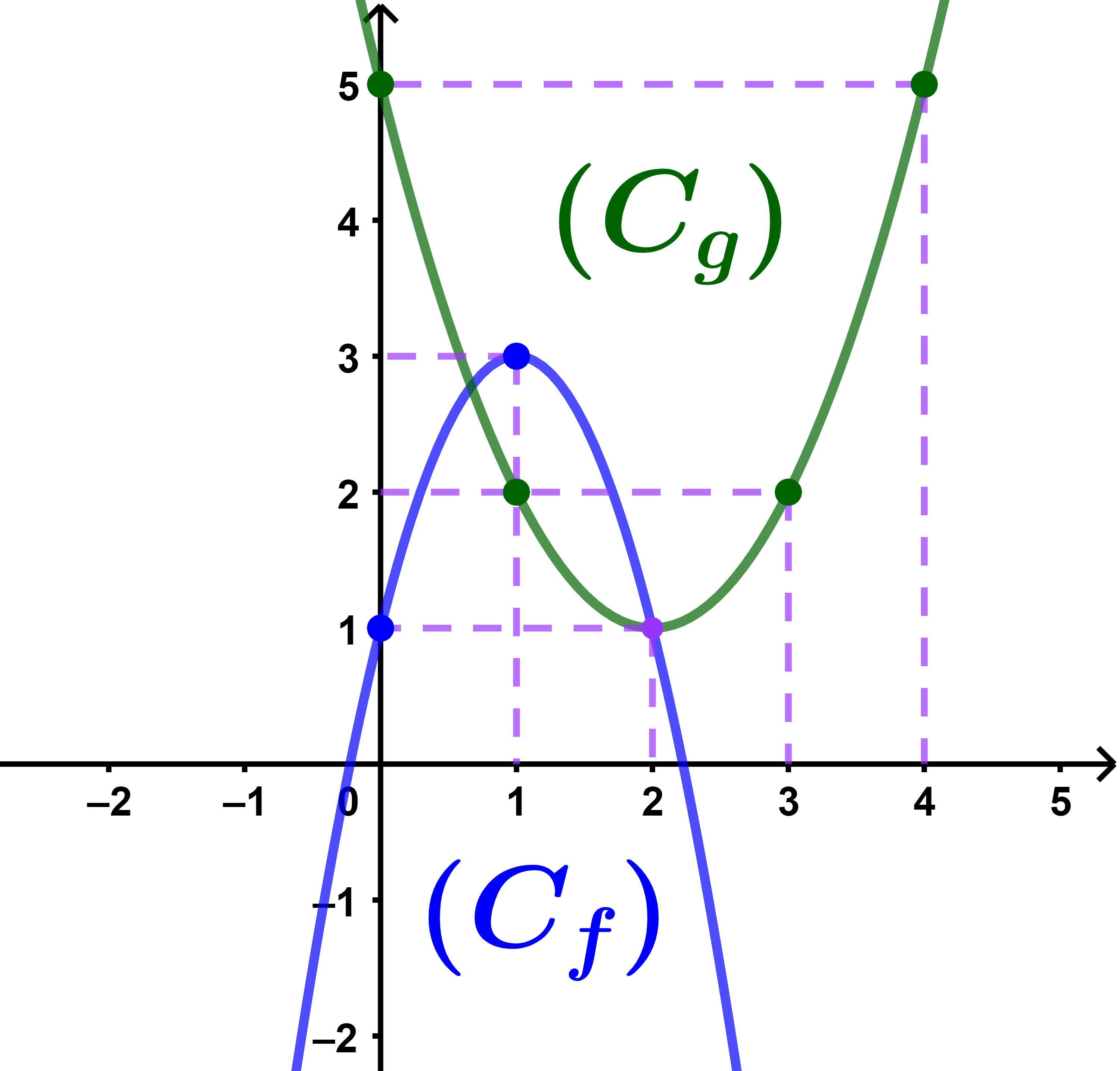
تمرين 3 tp

لتكن f و g دالتين عدديتين لمتغير حقيقي x ومعرفتين كما يلي
f(x)=2x²-4x+4.
و (C) المنحنى الممثل لها في معلم متعامد ممنظم (O;i^→;j^→).

et (C_f) و (C_g) المنحنيين الممثلين لهما على التوالي في معلم متعامد ممنظم (O;i^→;j^→).
1) (a) بين أن لكل x∈IR
لدينا f(x)=2(x-1)²+2.

(b) استنتج مطرافا للدالة f.
2) باستعمال المبيان المرفق.
(a) حل مبيانيا المعادلة f(x)=g(x).
(b) حل مبيانيا المتراجحة f(x)≥g(x).
(c) حل بيانيا وحسب قيم m المعادلة f(x)=m.