الدوال العددية (1)
1- التمثيل المبياني لدالة تآلفية
1.1 التمثيل المبياني لدالة خطية
1.1.1 تذكير
ليكن a عددا حقيقيا غير منعدما نقول ان f دالة خطية اذا كانت تكتب على الشكل f(x)=ax حيث x∈IR.
1.1.2 أمثلة
مثال 1
لتكن f دالة عددية معرفة كما يلي f(x)=2x
و (C) المنحنى الممثل لها في معلم متعامد ممنظم.
انشئ المنحنى (C) واستنتج رتابة f مبيانيا.
تصحيح
نحدد قيم بعض الصور بواسطة f
للتذكير ينبغي اختيار قيم مناسبة والتي تكون كافية لانشاء المنحنى
لايحبد اخذ قيم يصعب رسمها على الورقة
لنأخذ مثالا اذا وضعنا x=10 فان f(10)=20 !
واذا كان ولابد ينبغي تغيير وحدات المعلم.
| x | - 1 | 0 | 1 | 2 |
| f(x ) | - 2 | 0 | 2 | 4 |
ملاحظة نقط المنحنى (C) مستقيمية لان معادلة المنحنى
y=2x هي معادلة مستقيم مار من أصل المعلم
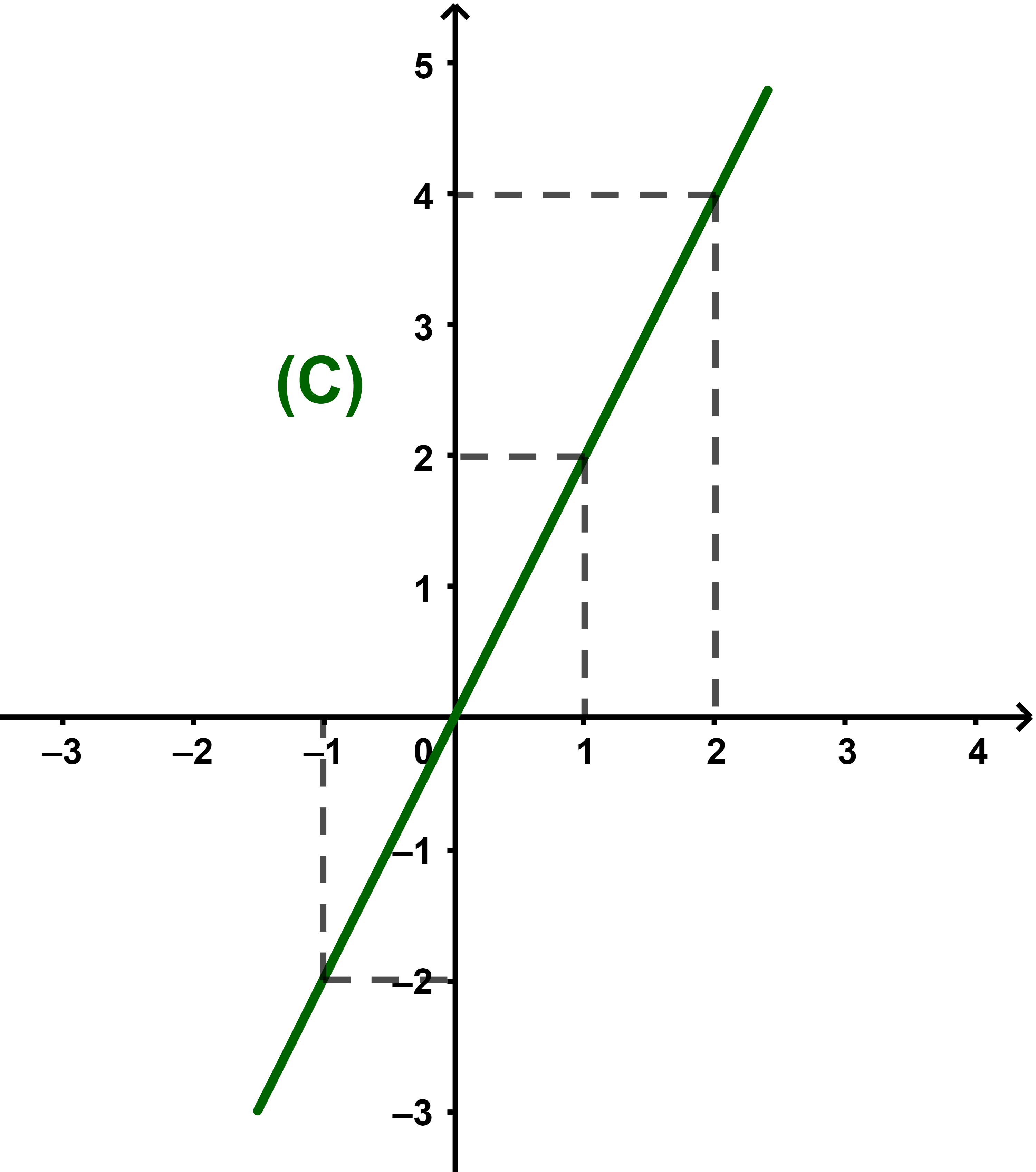
نحدد تغيرات الدالة f من خلال المنحنى
الدالة f تزايدية قطعا على IR.
| x | -∞ | +∞ | |
| f | ↗ |
مثال 2
لتكن g دالة عددية لمنغير x بحيث
| g(x) = | - 1 | x |
| 2 |
و (C) المنحنى الممثل لها في معلم متعامد ممنظم
انشئ المنحنى (C) واستنتج رتابتها مبيانيا.
تصحيح نحدد قيم بعض الصور بواسطة g
| x | - 2 | 0 | 2 |
| g(x ) | 1 | 0 | -1 |
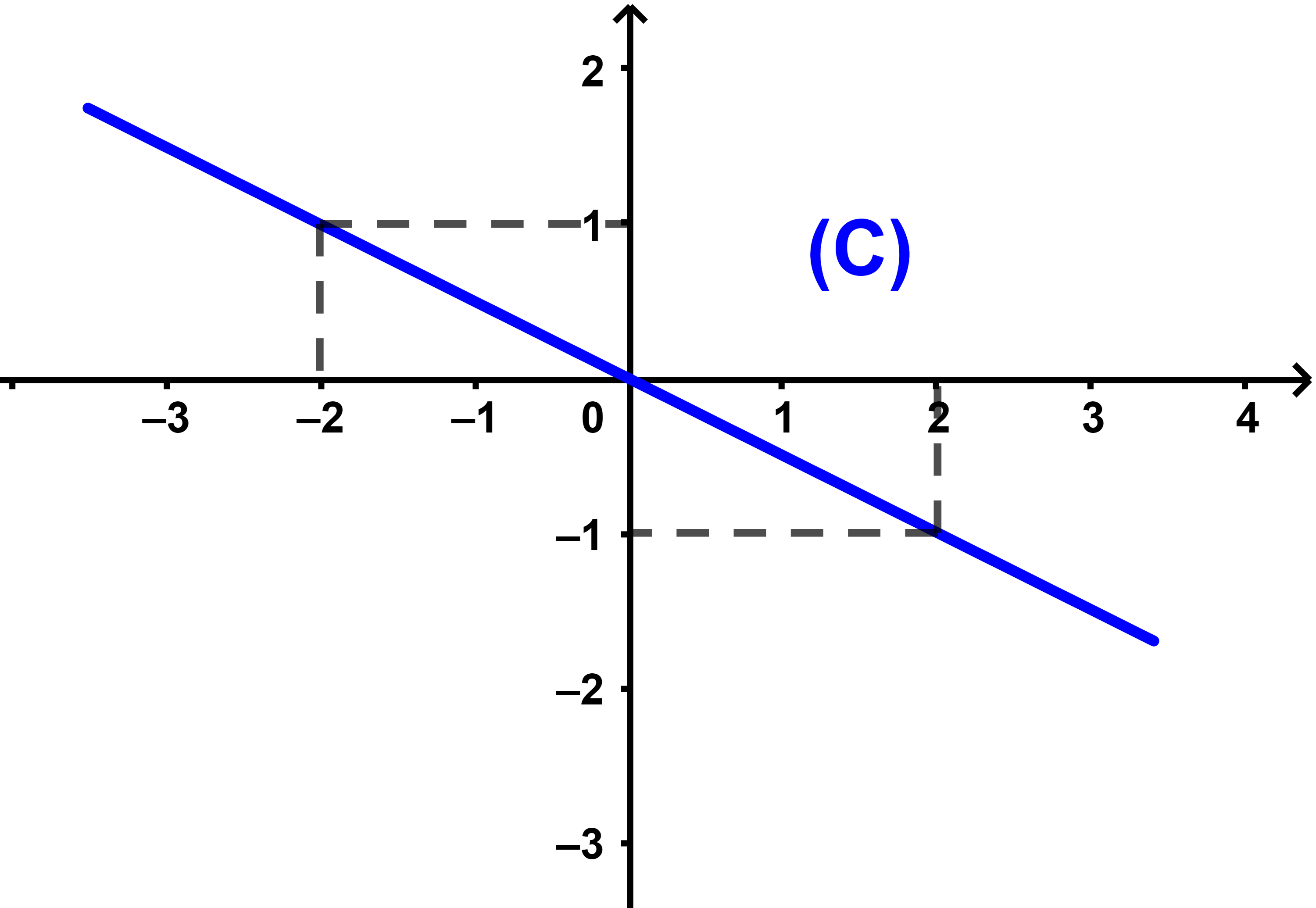
ملاحظة نقط المنحنى (C) مستقيمية لان معادلة المنحنى.
| y = | - 1 | x |
| 2 |
هي معادلة مستقيم مار من أصل المعلم.
نحدد تغيرات الدالة g من خلال المنحنى
الدالة g تناقصية قطعا على IR.
| x | -∞ | +∞ | |
| g | ↘ |
1.2.3 خاصية
ليكن a عددا حقيقيا غير منعدما
و f دالة خطية اي
f(x)=ax حيث x∈IR
منحنى الدالة f هو مستقيم معادلته y=ax.
1) اذا كان a>0 فان f دالة تزايدية قطعا على IR.
2) اذا كان a<0 فان f دالة تناقصية قطعا على IR.
تمرين 1 tp
لتكن f دالة عددية لمنغير x بحيث
| f(x) = | 1 | x |
| 4 |
و (C) المنحنى الممثل لها في معلم متعامد ممنظم.
1) بين أن f دالة تزايدية قطعا على IR.
2) انشئ المنحنى (C).