Mathématiques du secondaire qualifiant

1.2 التمثيل المبياني لدالة تآلفية

1.2.1 تذكير

ليكن a و b عددين حقيقيين بحيث a≠0
نقول ان f دالة تآلفية اذا كانت تكتب على الشكل
f(x)=ax+b.

1.2.2 أمثلة

مثال 1
f دالة عددية معرفة كما يلي f(x)=x+2
و (C) المنحنى الممثل لها في معلم متعامد ممنظم (O;i^→;j^→).
انشئ المنحنى (C).

كما اشرنا سابقا لرسم منحنى نحدد بعض صور مناسبة بواسطة الدالة لمعرفة شكل المنحنى

x	-2	0	1	2
f(x)	0	2	3	4

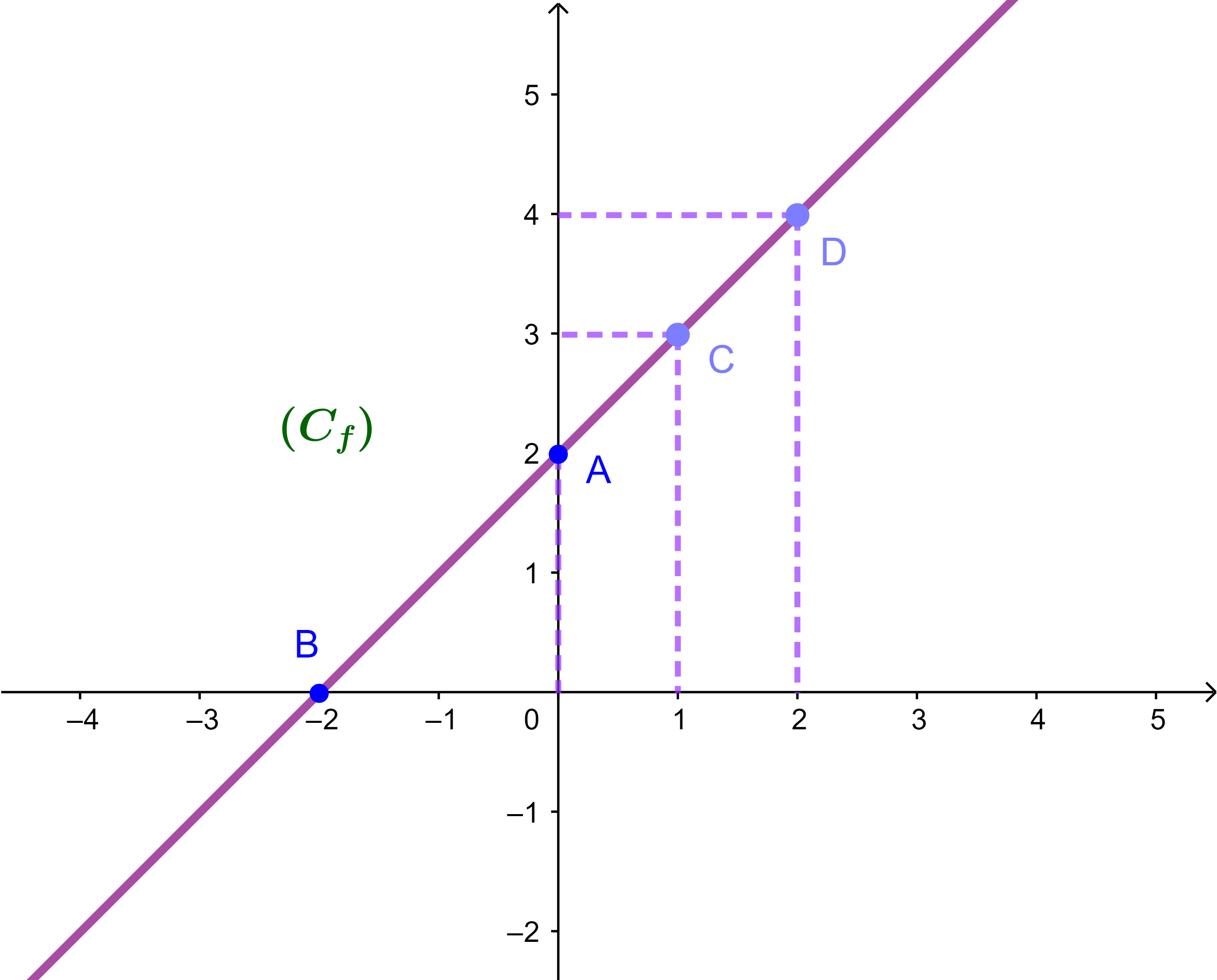
ملاحظة
النقط A و B و C و D تنتمي الى المنحنى (C) ومستقيمية اذن تحدد مستقيم منطبق مع المنحنى (C).

من خلال المنحنى الدالة f تزايدية قطعا على IR
جدول تغيرات الدالة f

x	-∞		+∞
f		↗

1.2.3 خاصية

ليكن a و b عددين حقيقيين بحيث a≠0
و f دالة تآلفية اي f(x)=ax+b حيث x∈IR
منحنى الدالة f هو مستقيم معادلته y=ax+b.
1) اذا كان a > 0 فان f دالة تزايدية قطعا على IR.
2) اذا كان a < 0 فان f دالة تناقصية قطعا على IR.

تمرين 1 tp

لتكن f دالة عددية لمتغير حقيقي x بحيث f(x)=-2x+2
و (C) المنحنى الممثل لها في معلم متعامد ممنظم
(O;i^→;j^→).
انشئ النحنى (C).

تصحيح

لدينا f دالة تآلفية و a=-2<0 اذن f دالة تناقصية قطعا على IR
والمنحنى (C) مستقيم ولرسمه يكفي تحديد نقطتيه منه.

x	0	1
f(x)	2	0