Fonctions numériques (9)
3.1.2 Exemple 2
Soit f une fonction numérique définie par
| f(x) = | -2 |
| x |
et (C) sa courbe représentative dans un repère orthonormé (O;i→;j→). Construire (C).
Correction
f est définie si x≠0
donc D=IR*=]-∞;0[∪]0;+∞[.
Etape 1: On sélectionne quelques images des abscisses convenables.
Notons que f est impaire donc il suffit de choisir des abscisses positives
mais nous choisissons les deux pour généraliser l'avantage.
| x | -4 | -2 | -1 | -0,5 | 0,5 | 1 | 2 | 4 |
| f(x) | 0,5 | 1 | 2 | 4 | -4 | -2 | -1 | -0,5 |
Etape 2: On consrtuit en général un repère orthonormé puis les points sélectionnés.
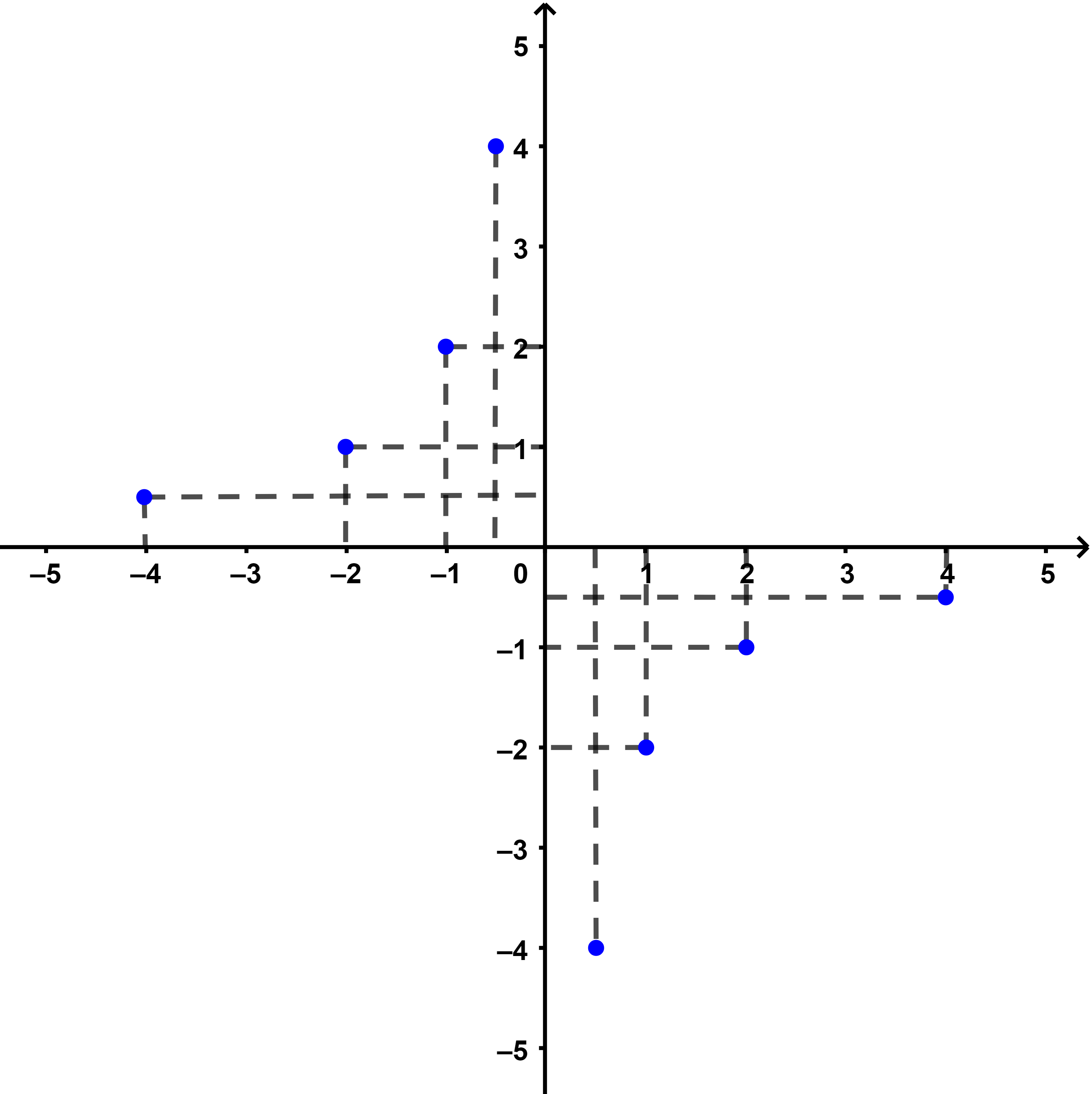
Etape 3: Dans un premier temps on relie ces points avec des pointiers.
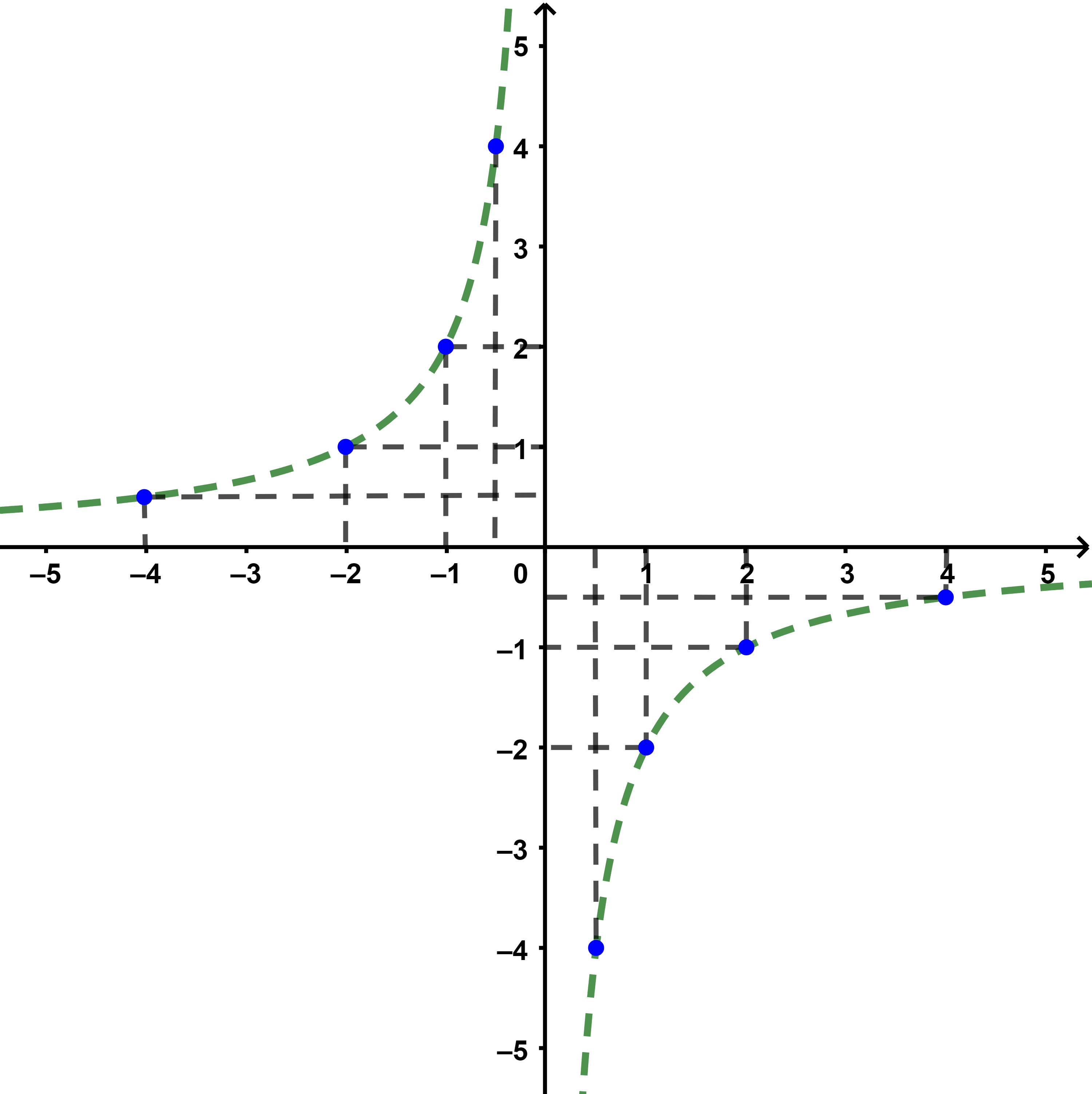
Etape 4: On relie ces points avec attention lorsque la courbe se rapproche des asymptotes sans se déformer.
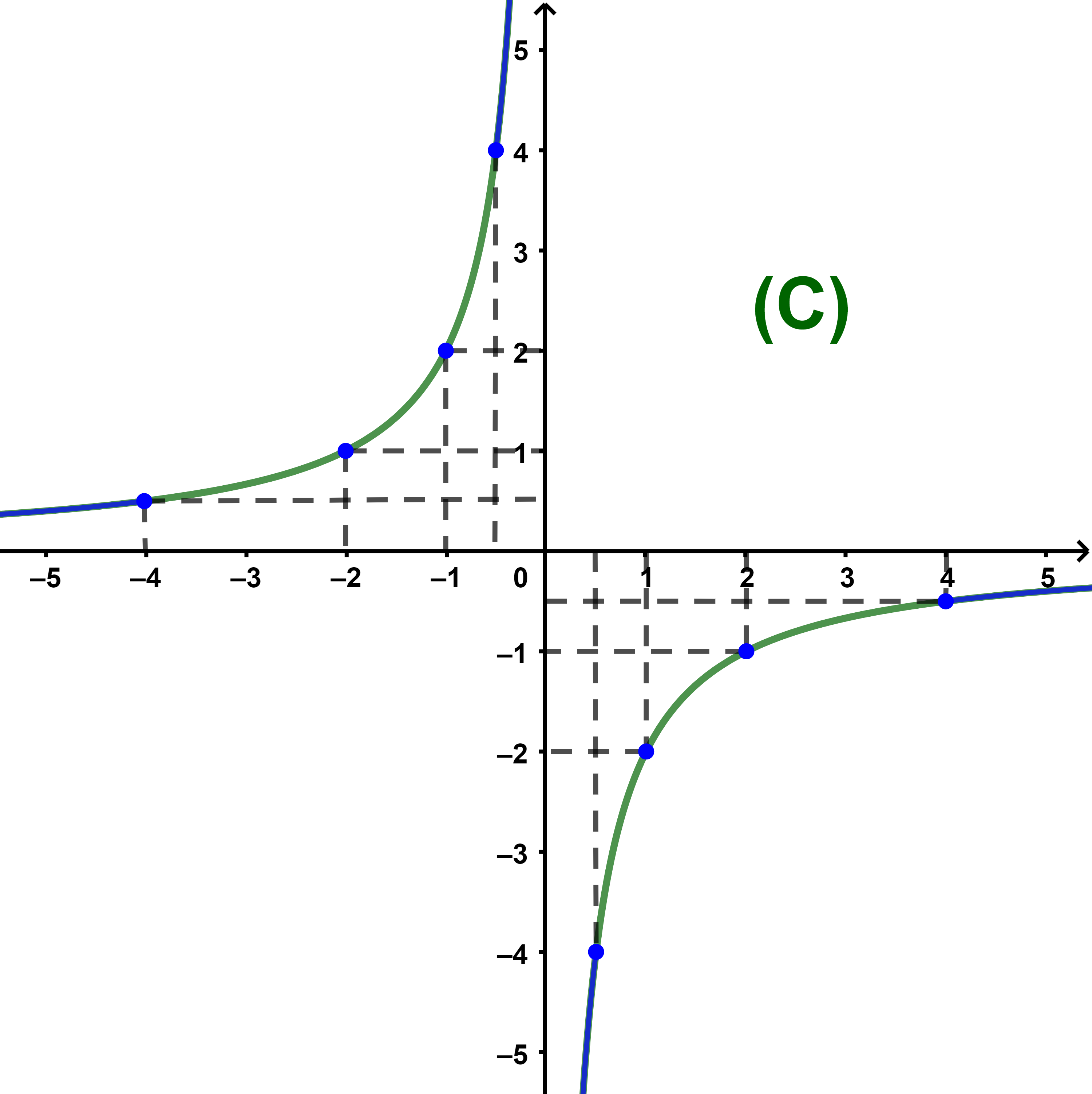
(C) est appelée hyperbole de centre O et admet deux asymptotes:
l'axe des abscisses et l'axe des ordonnées.
f est strictement croissante sur ]0;+∞[
et strictement croissante sur ]-∞;0[.
Tableau de variations
| x | -∞ | 0 | +∞ | |||
| f | ↗ | ↗ |
3.1.3 Propriété
Soit f une fonction numérique définie par
| f(x) = | a |
| x |
tel que a∈IR*
1) Si a>0 alors f est srictement décroissante sur IR+* et sur IR-*.
2) Si a<0 alors f est srictement croissante sur IR+* et sur IR-*.