تمرين 1 tp

لتكن f و g دالتين عدديتين معرفتين كما يلي

f(x) =	x		g(x) =	-x
	2x+2			x+1

1) حدد D_f و D_g على التوالي مجموعتي تعريف f و g.

(C_f) و (C_g) على التوالي المنحنيان للدالتين f و g في المعلم متعامد ممنظم (O;i^→;j^→).

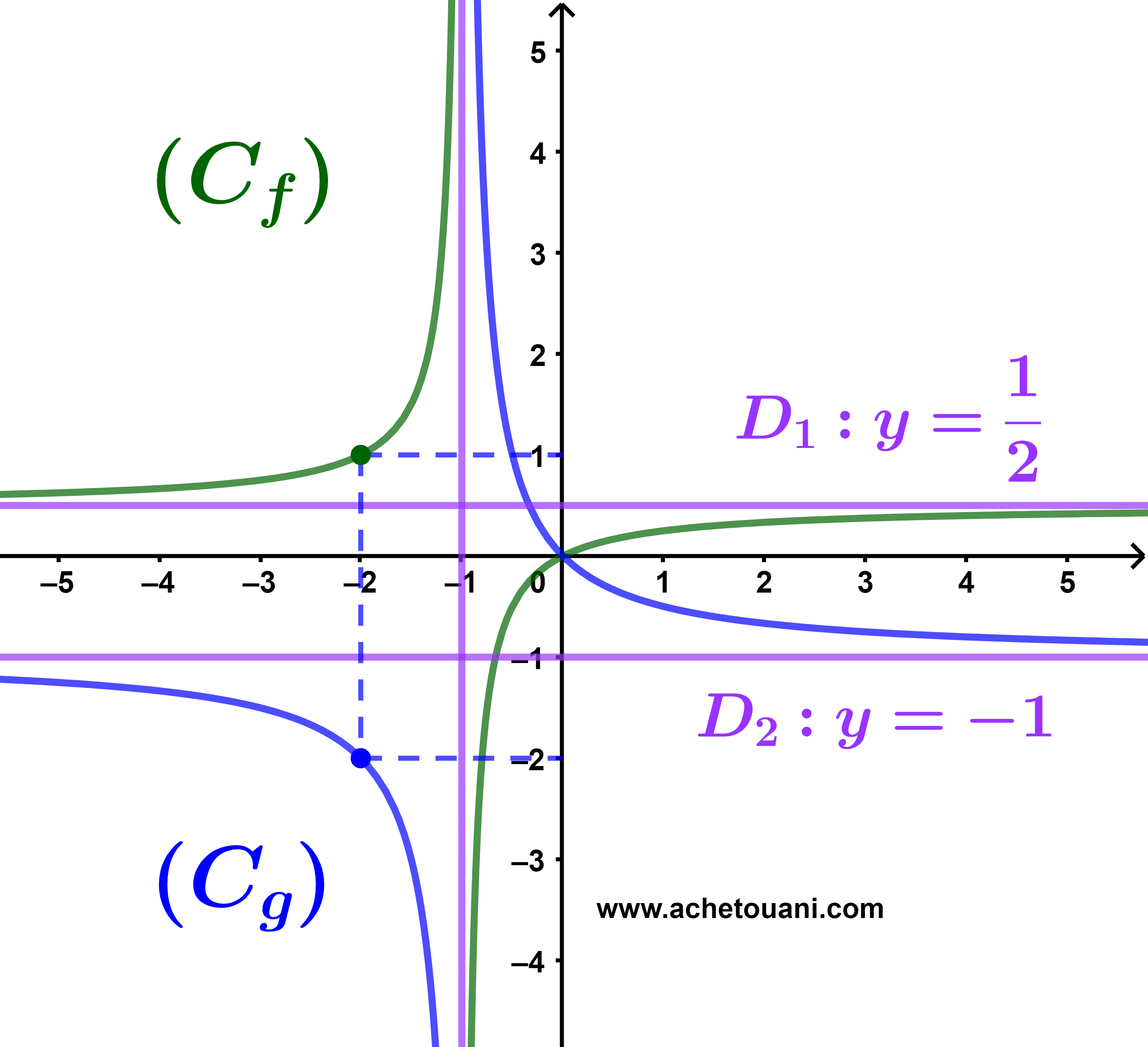
2) حدد مبيانيا تغيرات الدالتين f و g وأنشئ جدول تغيراتهما.
3) حدد هندسيا اشارة f(x).
4) حل في D المعادلة f(x)=g(x).
5) حل مبيانيا المتراجحة f(x)≤g(x).
استنتج مجموعة حلول المتراجحة f(x)>g(x).

تمرين 2 tp

لتكن f و g دالتين عدديتين معرفتين بمنحنياهما التاليين.

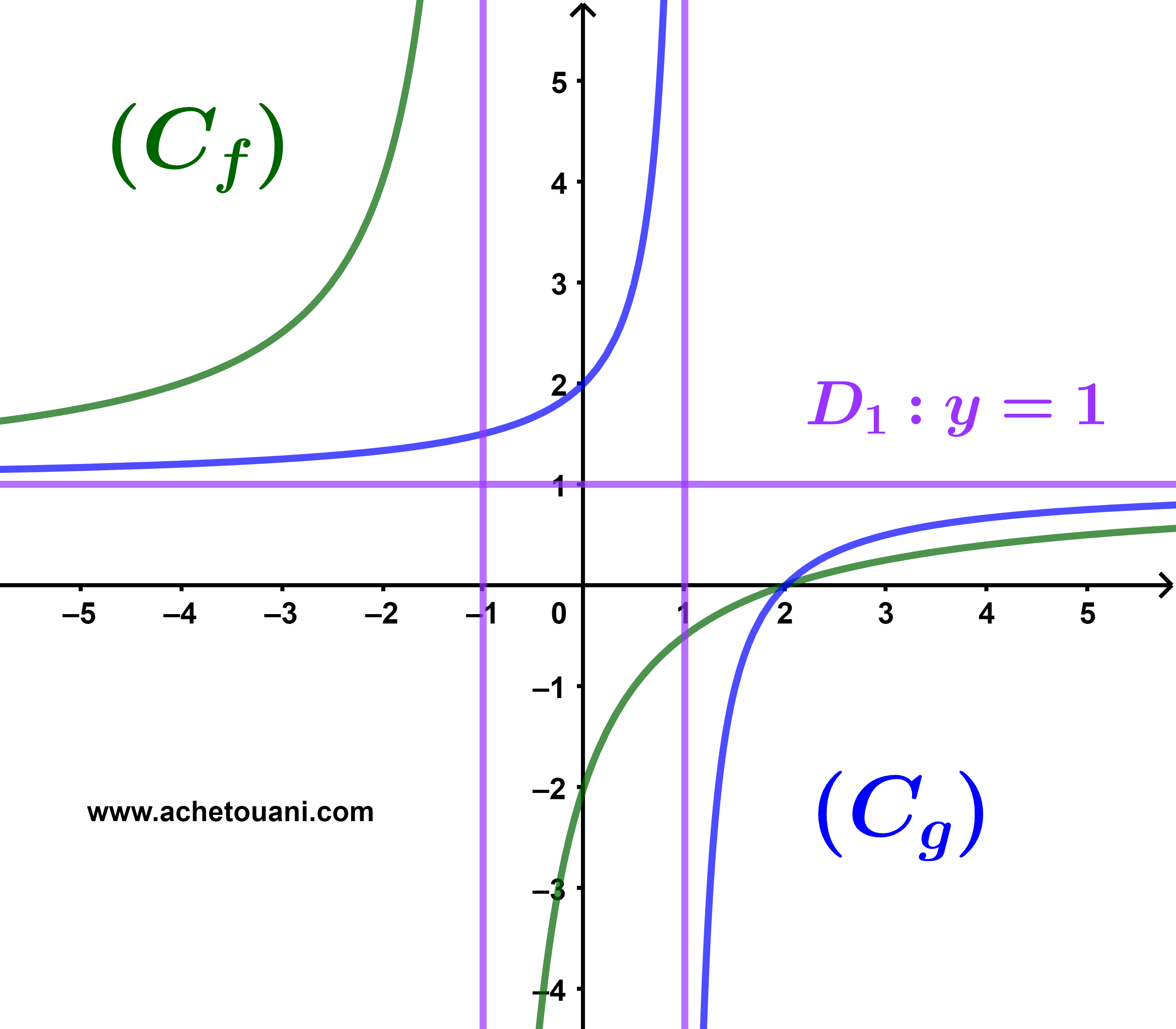
حل مبيانيا المتراجحة
f(x)≤g(x).

تمرين 3 tp

حل مبيانيا المتراجحة التالية

x	≤x²-4x
x-2

تمرين 4 tp

1) أنشئ المنحنى الممثل للدالة cosinus على المجال [0;π].
2) أنشئ جدول التغيرات للدالة cosinus على المجال

[	π	;	5π	]
	2		2

2) استنتج التغيرات على المجال

[	-5π	;	-π	]
	2		2

.