الدوال العددية (13)
تمرين 1 tp
f دالة عددية معرفة كما يلي
| f(x) = | -x+1 |
| x |
و (Cf) منحناها في المعلم متعامد ممنظم
(O;i→;j→).
1) حدد Df مجموعة تعريف الدالة f
2) (a) بين ان الدالة f تناقصية قطعا على
]-∞;0[
وعلى
]0;+∞[
(b) انشئ جدول تغيرات الدالة f.
3) حل في Df المعادلة f(x)=-2
4) (a) انشئ المنحنى (C).
(b) حدد اشارة f(x) على Df
5) نعتبر الدالة g المعرفة كما يلي
| g(x) = | -x+1 | ||
| x |
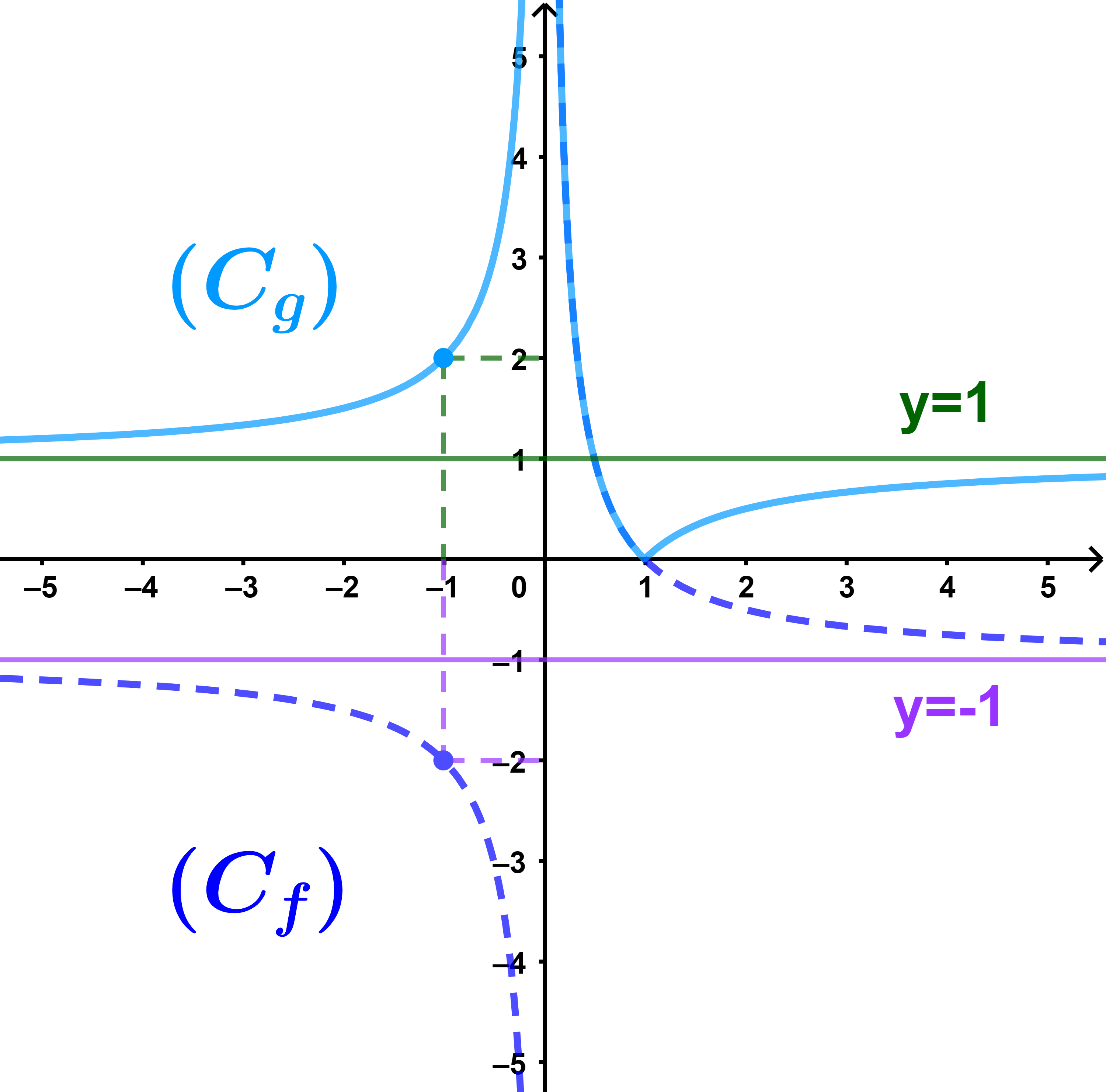
انشئ في نفس المعلم (Cg) منحنى الدالة g
تصحيح
1) f معرفة يعني x≠0 اذن D=IR*.
2) (a) f دالة متخاطة اذن دالة مرجعية
وبما ان ad-bc=-1 < 0 فان الدالة f تناقصية قطعا على
]-∞;0[
وعلى
]0;+∞[
(b) جدول التغيرات
| x | -∞ | 0 | +∞ | ||||
| f | -1 | ↘ |
|| | ↘ |
-1 |
3) ليكن x∈D اذن x≠0
f(x)=-2 يعني
-x+1=-2x
يعني
-x+2x=-1
يعني
x=-1
وبما ان
(-1)∈D فان
S={-1}.
4) (a) مقاربات المنحنى (C)
المنحنى (C) هذلول احداثيات مركزه
| ( | -d | ; | a | ) | = ( | -(0) | ; | -1 | ) |
| c | c | 1 | 1 |
اذن W(0;-1) ويقبل مقاربين (D1) و (D2)
| (D1): x = | -d | و (D2): y = | a |
| c | c | ||
| (D1): x = | 0 | و (D2): y = | -1 |
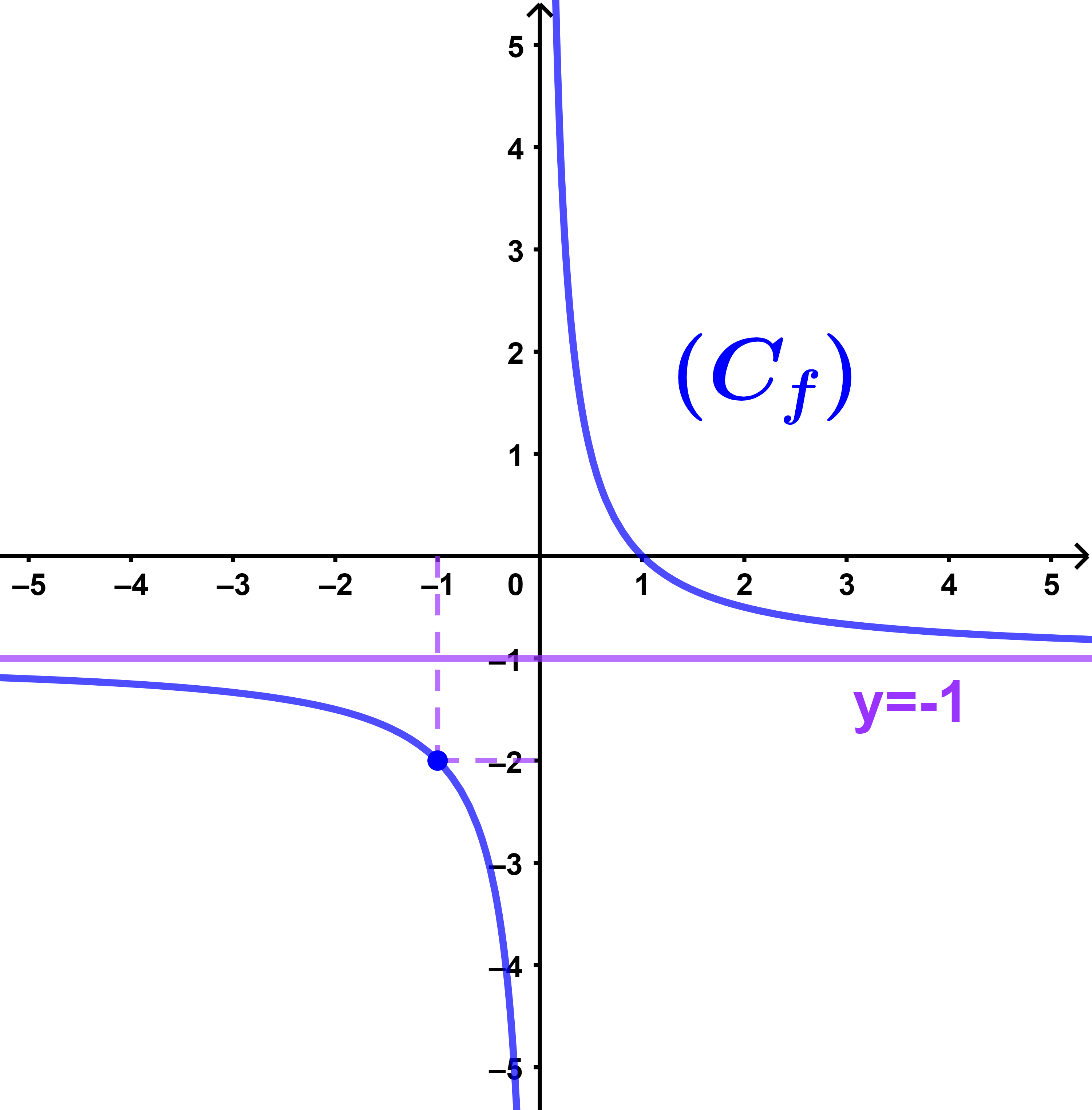
(b) اشارة f(x)
f(x)≥0 يعني المنحنى (Cf) فوق محور الافاصيل
اذن f(x)≥0 يعني
x∈]0;1].
f(x)≤0 يعني ان المنحنى تحت محور الافاصيل
اذن f(x)≤0 يعني
x∈]-∞;0[∪[1;+∞[.
| x | - ∞ | 0 | 1 | +∞ | |||
| f(x) اشارة | - | || | + | 0 | - |
5) لدينا g(x)=|f(x)|
لدينا Dg=Df
اذا كانت f(x)≥0 فان g(x)=f(x)
واذا كانت f(x)≤0 فان g(x)=-f(x)
وهذا يعني ان المنحنى (Cg) منطبق مع المنحنى (Cf) في المجال
]0;1]
والمنحنى (Cg) متماثل مع المنحنى (Cf) بالنسبة لمحور الافاصيل في المجالين
]-∞;0[
و
[1;+∞[.