الدوال العددية (1)
تذكير الدالة التآلفية
لتكن a و b عددين حقيقيين بحيث والدالة f التآلفية f المعرفة ب
f(x)=ax+b و
1) المنحنى (C) هو مستقيم معادلته y=ax+b.
2) اذا كان a>0 فان f تزايدية قطعا على IR.
3) اذا كان a<0 فان f تناقصية قطعا على IR.
تمرين 1 tp
لتكن f دالة عددية معرفة ب f(x)=-2x+1.
و (C) المنحنى الممثل لها في امعلم (O;i→;j→). أنشئ (C).
تصحيح
f دالة تآلفية و a=-2<0 اذن f تناقصية قطعا على IR.
المنحنى (C) هو مستقيم اذن يكفي حساب صورتين لانشاء المنحنى.
| x | 0 | 1 |
| f(x) | 2 | 0 |

تمرين 2 tp
لتكن f دالة خطية معرفة ب
| f(x) = | 1 | x |
| 4 |
و (C) المنحنى الممثل لها في امعلم (O;i→;j→).
1) بين أن f تزايدية قطعا على IR.
2) أنشئ (C).
تمرين 3 tp
لتكن f دالة عددية معرفة ب f(x)=x+2
و (C) المنحنى الممثل لها في امعلم (O;i→;j→). أنشئ (C)
بتعيين قيم افاصيل مناسبة لبعض نقط المنحنى لمعرفة الشكل.
| x | -2 | 0 | 1 | 2 |
| f(x) | 0 | 2 | 3 | 4 |
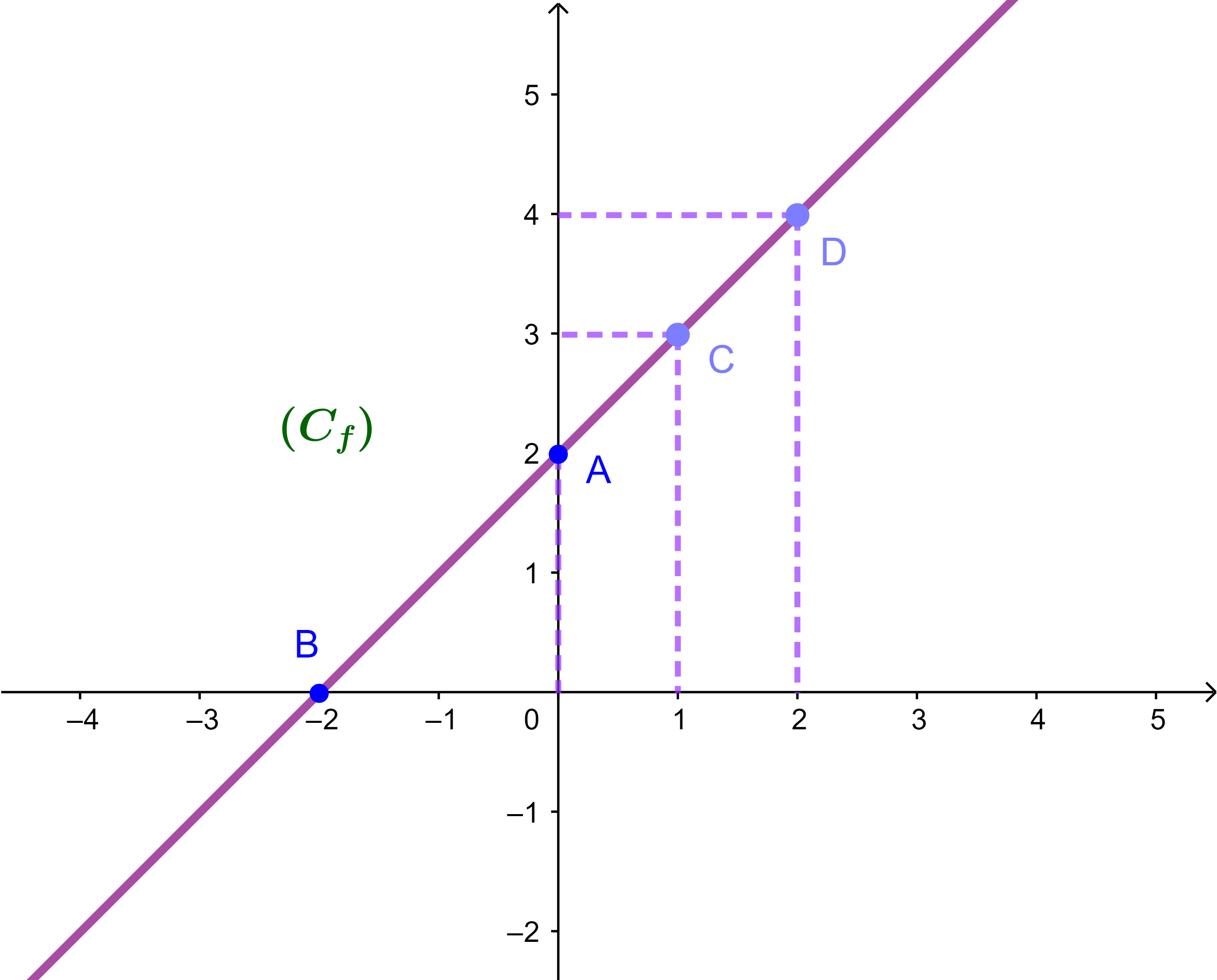
نقط المنحنى (C) مستقيمية
اذن تكون مستقيم.
هندسيا f تزايدية قطعا على IR
| x | -∞ | +∞ | |
| g | ↗ |
تمرين 4 tp
لتكن f و g دالتين عدديتين بحيث
f(x)=2x-3 و g(x)=-2x+1.
(Cf) و (Cg) منحنيانها على التوالي في المعلم (O;i→;j→).
1) انشئ (Cf) و (Cg) في نفس المعلم.
2) حدد هندسيا نقطة تقاطع (Cf) و (Cg).