الدوال العددية (2)
تمرين 1 tp
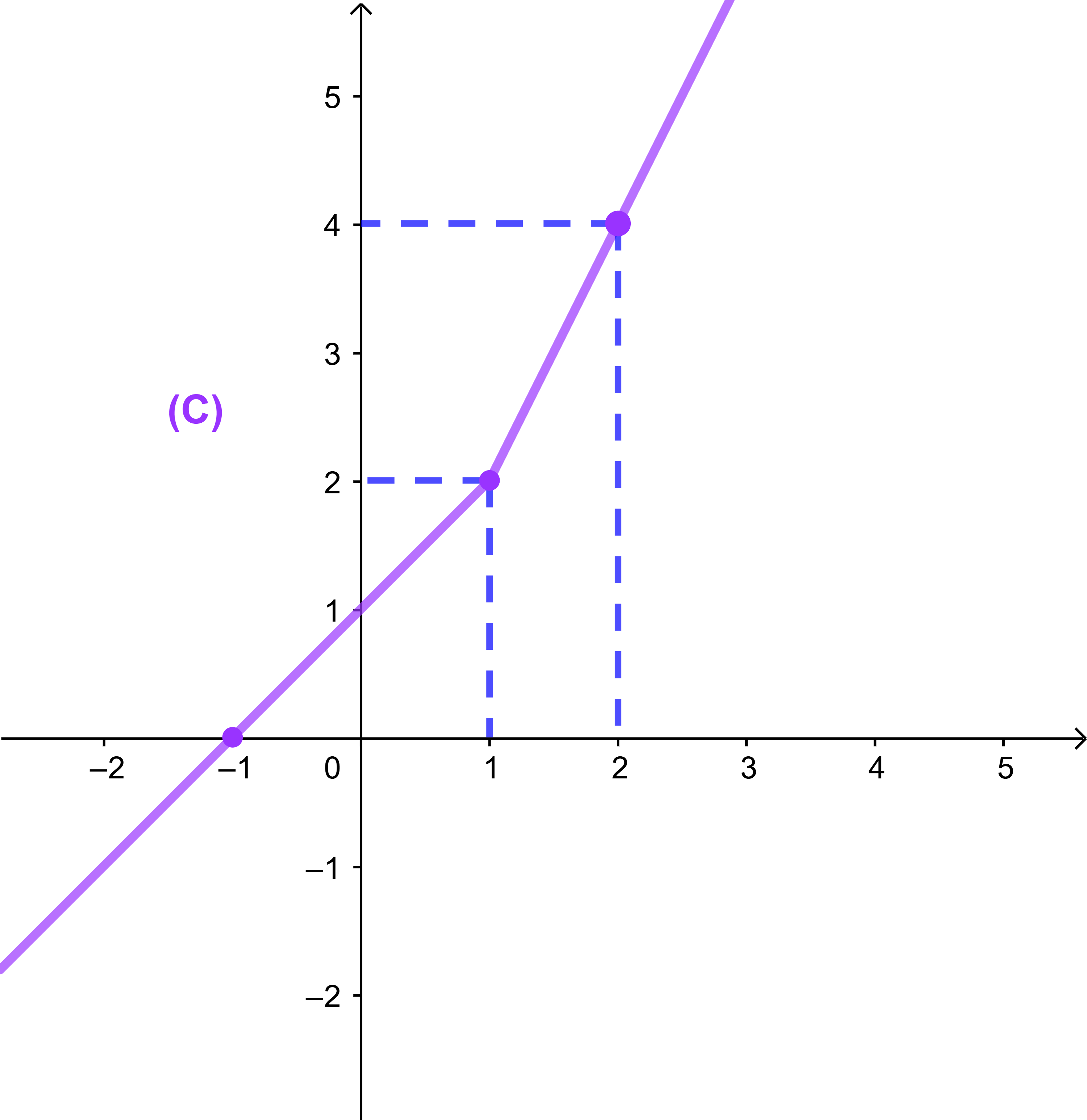
لتكن f دالة عددية معرفة ب f(x)=-2x+2.
و (C) المنحنى الممثل لها في امعلم (O;i→;j→).
1) ادرس تغيرات الدالة f.
2) حدد تقاطع المنحنى (C) ومحور الأفاصيل (Ox).
3) حدد تقاطع المنحنى (C) ومحور الأراتيب (Oy).
4) أنشئ (C).
تصحيح
1) a=-2<0 اذن f تناقصية قطعا على IR.
2) M(x;y)∈(C)∩(Ox) يعني y=0
يعني
-2x+2=0 يعني x=1.
اذن (C)∩(Ox)={A(1;0)}.
3) M(x;y)∈(C)∩(Oy) يعني x=0
اذن يكفي حساب f(0)
f(0)=-2.0+2=2
وبالتالي (C)∩(Oy)={B(0;2)}.

تمرين 2 tp
لتكن f دالة عددية معرفة بأجزاء
| { | f(x) = 2x | / x≥1 |
| f(x) = x+1 | / x< 1 |
و (C) المنحنى الممثل لها في امعلم (O;i→;j→).
أنشئ المنحنى (C).
تصحيح
f دالة عددية معرفة بأجزاء.
1) اذا كان x∈]-∞;1[ فان f(x)=x+1.
2) اذا كان x∈[1;+∞[ فان f(x)= 2x.
المنحنى (C) هو اذن اتحاد نصفي مستقيمين.
(D1): y=x+1 / x<1.
(D2): y=2x / x≥1.
تمرين 3 tp
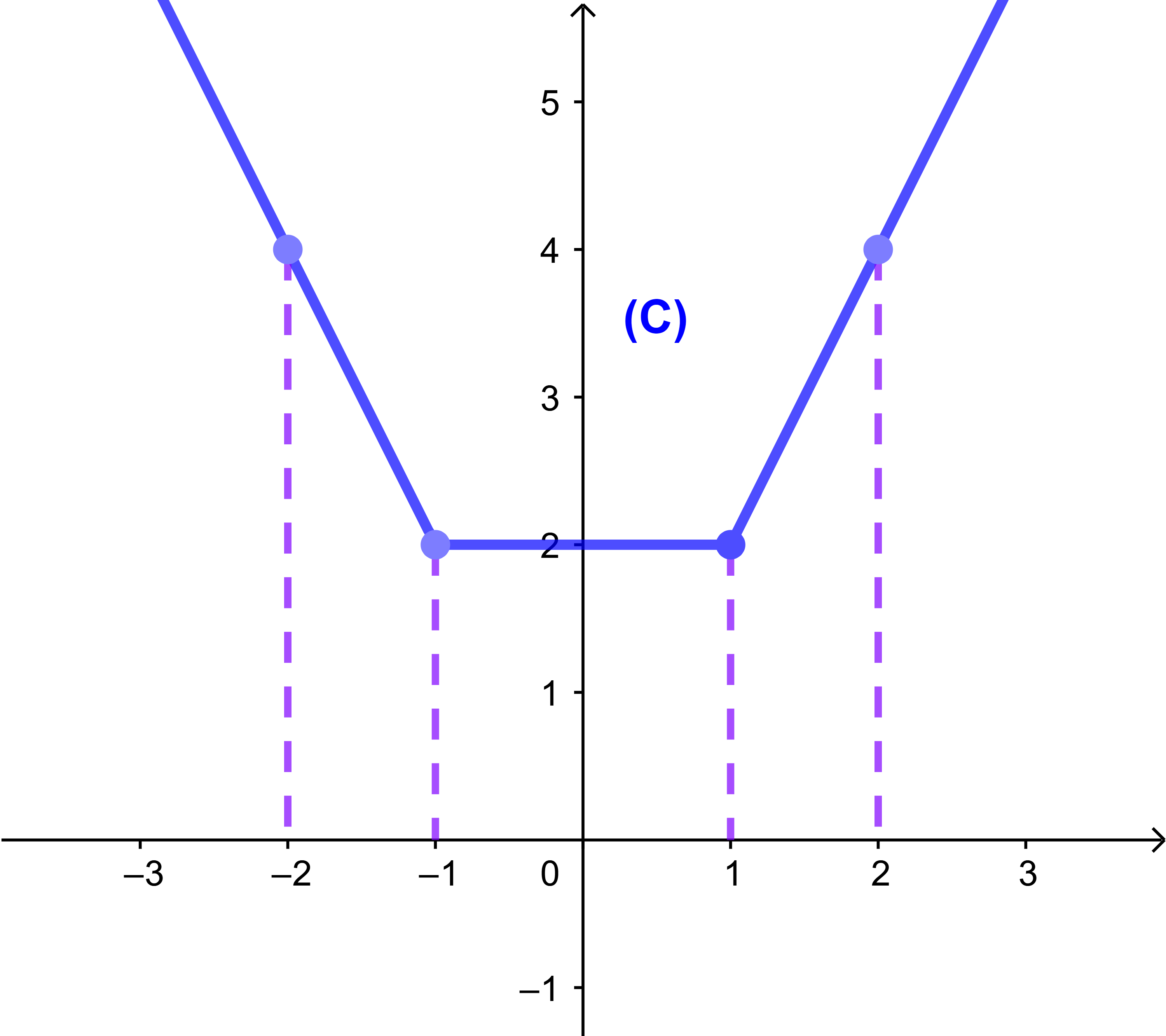
لتكن f دالة عددية معرفة ب
f(x)=|x-1|+|x+1| و (C) المنحنى الممثل لها في امعلم (O;i→;j→).
1) أكتب f(x) بدون استعمال القيمة المطلقة.
2) أنشئ المنحنى (C).
تصحيح
نترك لك دراسة اشارة x-1 و x + 1 على المجالات ]-∞;-1[ و [-1;1] و [1;+∞[.
| { | f(x) = 2x | / x > 1 |
| f(x) = 2 | / -1≤x≤1 | |
| f(x) = -2x | / x < -1 |