Fonctions numériques (1)
Rappel Fonctions affines.
Soient a et b deux nombres réels tel que a≠0
et la fonction affine f définie par
f(x)=ax+b et (C) sa courbe représentative dans un repère (O;i→;j→).
1) La courbe (C) est une droite d'équation y=ax+b.
1) Si a>0 alors f est strictement croissante sur IR.
2) Si a<0 alors f est strictement décroissante sur IR.
Exercice 1 tp
Soit f une fonction définie par f(x)=-2x+1
et (C) sa courbe représentative dans un repère (O;i→;j→). Construire (C).
Correction
f est une fonction affine et a=-2<0 donc f est strictement décroissante sur IR.
La courbe (C) est une droite il suffit donc de calculer deux images pour la construire.
| x | 0 | 1 |
| f(x) | 2 | 0 |

Exercice 2 tp
Soit f une fonction linéaire de la variable réel x définie par
| f(x) = | 1 | x |
| 4 |
et (C) sa courbe représentative dans un repère orthonormé (O;i→;j→).
1) Montrer que f est strictement croissante sur IR.
2) Construire (C).
Exercice 3 tp
Soit f une fonction définie par f(x)=x+2
et (C) sa courbe représentative dans un repère (O;i→;j→). Construisons (C) en détérminant quelques images convenables pour connaitre l'allure.
| x | -2 | 0 | 1 | 2 |
| f(x) | 0 | 2 | 3 | 4 |
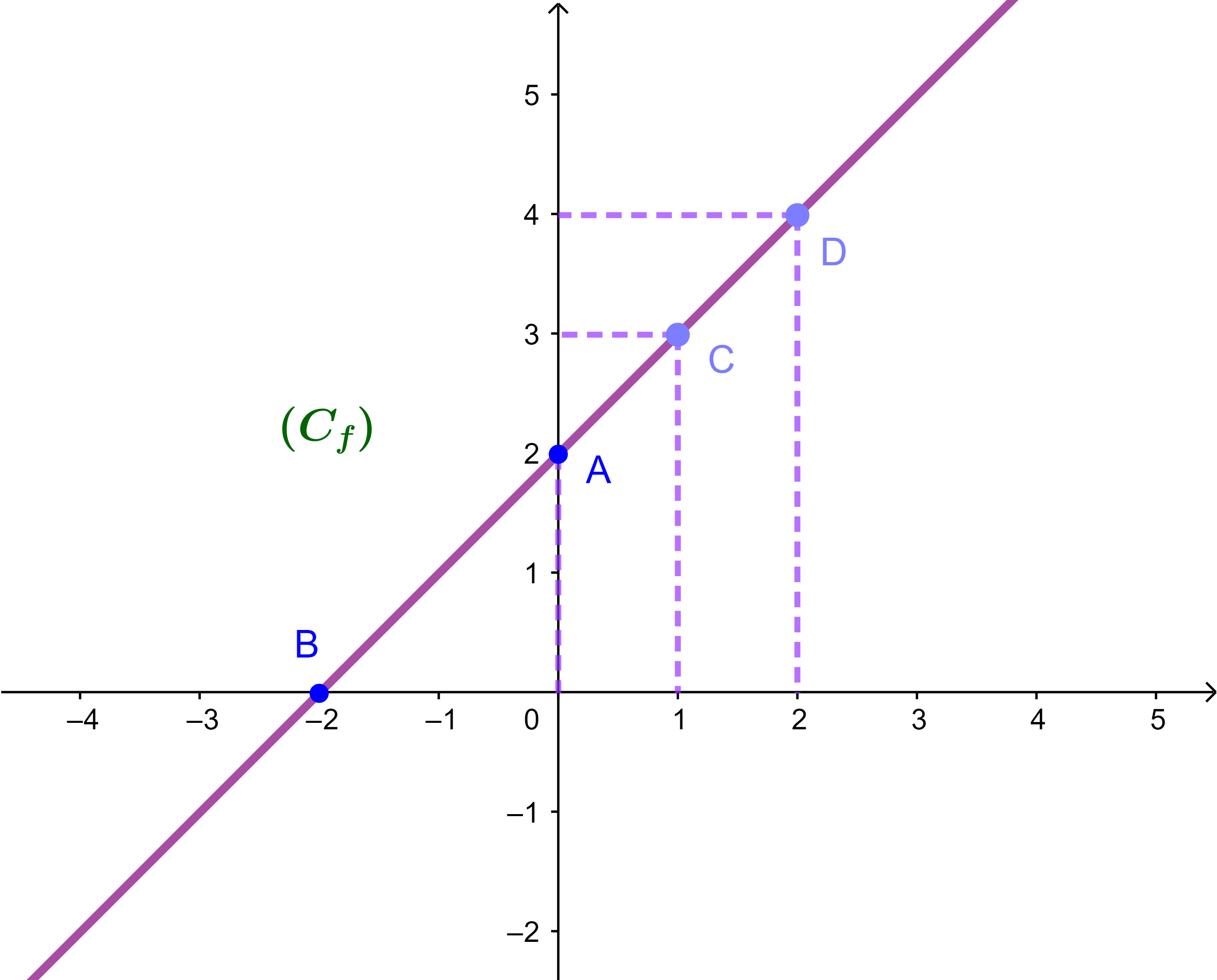
Les points de la courbe (C) sont alignés
donc ils forment une droite.
Graphiquement f est strictement croissante sur IR
| x | -∞ | +∞ | |
| g | ↗ |
Exercice 4 tp
Soient f et g deux fonctions définies par
f(x)=2x-3 et g(x)=-2x+1.
(Cf) et (Cg) leurs courbes représentatives respéctivement dans un repère (O;i→;j→).
1) Construire (Cf) et (Cg) dans le même repère.
2) Déterminer Graphiquement le point d'intersection de (Cf) et (Cg).