تمرين 1 tp

لتكن f دالة عددية لمتغير حقيقي x
بحيث f(x)=-x²+4x و (C) المنحنى الممثل لها في معلم متعامد ممنظم (O;i^→;j^→).
1) (a) بين أن لكل x∈D
f(x)=-(x-2)²+4
(b) استنتج أن 4 مطراف للدالة f.
2) انشئ المنحنى (C).

3) (a) استنتج هندسيا تغيرات f.
(b) انشئ جدول تغيرات f.
4) (a) حل مبيانيا المعادلة (E): f(x)=0.
(b) حل مبيانيا المتراجحة (I1): f(x)≤0.
(c) حل مبيانيا نظمة متراجحات
(I2) 3≤f(x)≤4.

تصحيح

1) (a) f حدودية اذن D=IR=]-∞;+∞[. ليكن x∈IR
f(x)=-x²+4x=-(x²-4x)
=-(x²-2.2x+2²-2²)=-(x-2)²+4
اذن لكل x∈IR لدينا f(x)=-(x-2)²+4.
(b) لكل x∈IR لدينا -(x-2)²≤0
يعني -(x-2)²+4≤4 يعني f(x)≤4
لاحظ أن f(2)=4 اذن 4 قيمة قصوى للدالة f عند 2.

2) المنحنى (C).
لدينا f(x)=-(x-2)²+4 و f(x)≤4
وهذا يعني أن أراتيب نقط المنحنى أصغر من أو تساوي 4.
أكبر أرتوب اذن هو العدد 4 اذن جميع نقط المنحنى توجد تحت النقطة W(2;4).

نحدد بعض صور مناسبة بواسطة الدالة لمعرفة شكل المنحنى (C).

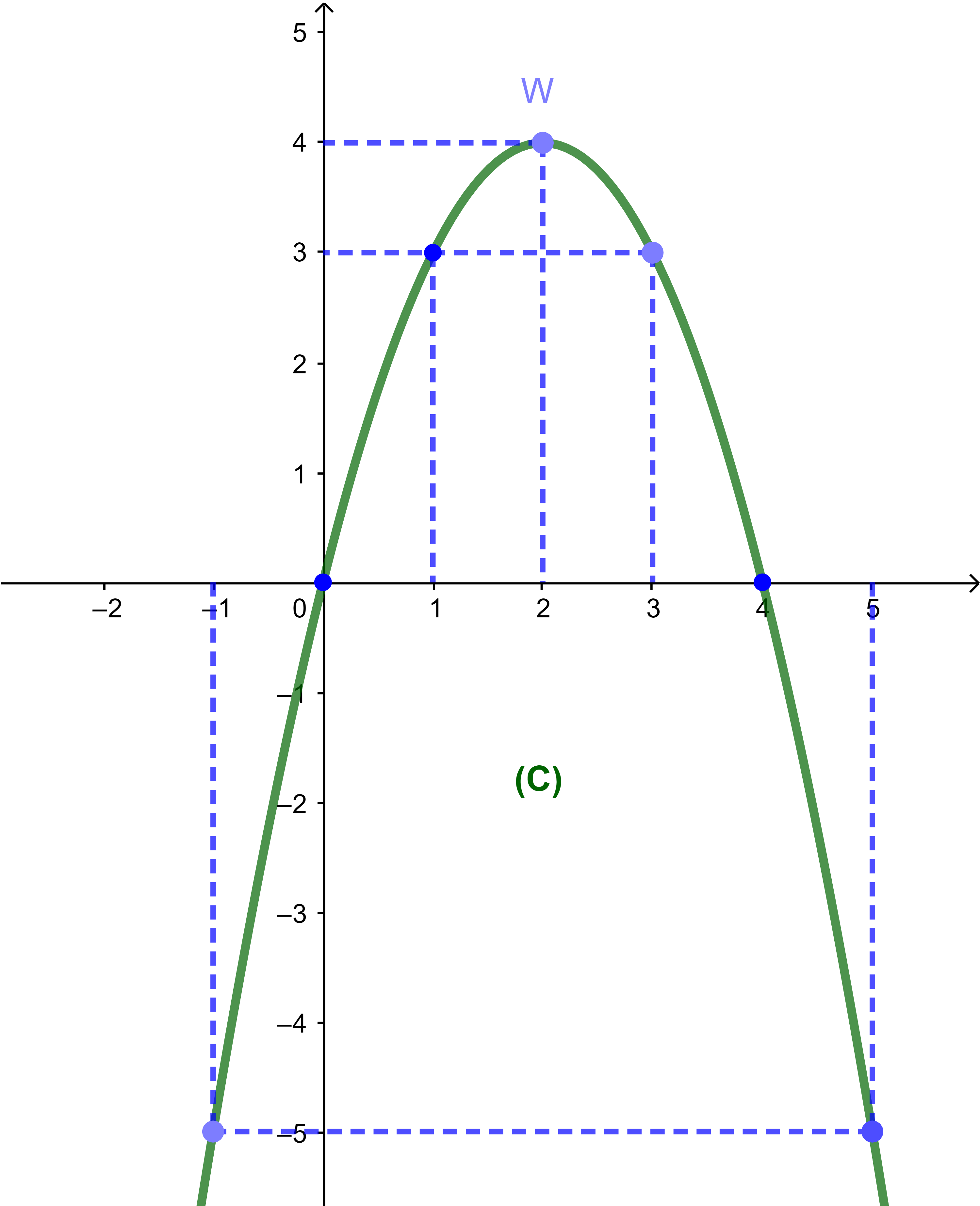
3) (a) هندسيا f تزايدية قطعا على ]-∞;2]
وتناقصية قطعا على [2;+∞[
(b) جدول تغيرات f.

4) (a) حل المعادلة f(x)=0 هندسيا هو تحديد عدد نقط تقاطع المنحنى (C) ومحور الأفاصيل (Ox).
المنحنى (C) يقطع المحمر (Ox) في نقطتين اذن المعادلة f(x)=0 تقبل حلين
هما 0 و 4 وبالتالي S={0;4}.
(b) حل المتراجحة f(x)≤0 مبيانيا يعني تحديد المجال أو المجالات
بحيث يكون المنحنى (C) تحت محور الأفاصيل (Ox) في المجالين
]-∞;0] و [4;+∞[
المنحنى (C) تحت المحور (Ox) اذن مجموعة حلول المتراجحة
S₁=]-∞;0]∪[4;+∞[.

(c) 3≤f(x)≤4 هندسيا يعني تحديد المجالات
بحيث يكون المنحنى (C) بين المستقيمين (D₁):y=3 و (D₂):y=4.
لاحظ أن f(1)=3 و f(2)=4 و f(3)=3.
إذا أسقطنا الجزء الصغير من الشلجم على محور الأفاصيل بين المستقيمين (D₁) و (D₂)
فسنحصل على قطعة ممثلة بالمجال [1;3]
وبالتالي مجموعة الحلول S₂=[1;3].