تمرين 1 tp

لتكن f دالة عددية معرفة ب
f(x)=2x²-4x+1 و (C) المنحنى الممثل لها في معلم متعامد ممنظم
(O;i^→;j^→).
1) حدد D مجموعة تعريف الدالة f.
2) (a) انشئ النحنى (C).
(b) أنشئ جدول تغيرات f.
3) (a) حل مبيانيا المعادلة (E):f(x)=0.
(b) حل مبيانيا المتراجحة (I):f(x)≤0.

تصحيح

1) f حدودية اذن D=IR.
2) (a) المنحنى (C).
f حدودية من الدرجة الثانية اذن (C) شلجم رأسه

w(	-b	;	f(	-b	))
	2a			2a

ومنه فان w(1;-1).
نحدد بعض صور مناسبة بواسطة الدالة لمعرفة شكل منحنى الدالة f

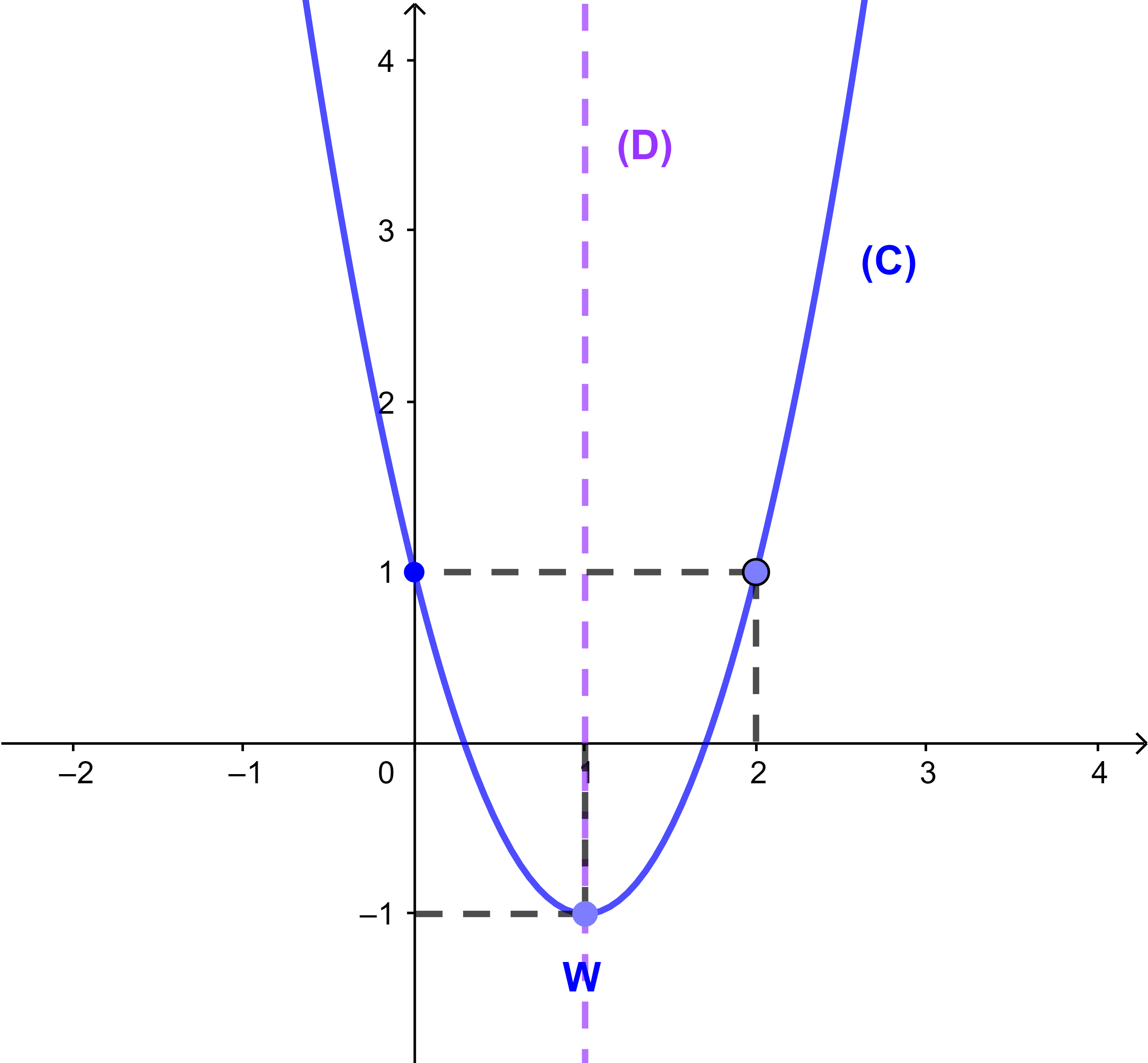
انطلاقا من المنحنى الدالة f تناقصية قطعا على المجال
]-∞;1[ وتزايدية قطعا على المجال ]1;+∞;].
(b) جدول التغيرات

x		-∞		1		+∞
f			↘	-1	↗

(b) حلول المعادلة f(x)=0.
عدد نقط تقاطع (C) ومحور الأفاصيل هو 2 اذن المعادلة f(x)=0 تقبل حلين u و v
بحيث 0 <u<1 و 1<v<2.

(c) حلول المتراجحة f(x)≤0 نحدد المجالات بحيث يكون المنحنى (C) تحت محور الأفاصيل.
في المجال [u;v] المنحنى (C) تحث (Ox)
اذن مجموعة حلول المتراجحة f(x)≤0
S=[u,v] بحيث u و v حلان للمعادلة f(x)=0.