Rappel Fonctions de référence.
La fonction homographique f est une fonction définie par

f(x) =	ax+b
	cx+d

tels que a;b;c et d sont des constantes et c≠0. et (C) sa courbe représentative dans un repère orthonormé (O;i^→;j^→).
1) (C) est une hyberbole de centre W

W(	-d	;	a	)
	c		c

2) (C) admet deux asymptotes

(D): x=	-d	et (D'): y=	a
	c		c

Exercice 1 tp

Soit f une fonction numérique définie par

f(x) =	-2x+1
	x-1

D={x∈IR /x-1≠0 }=]-∞;1[∪]1;+∞[
(C) est une hyperbole de centre W(1;-2).
f est strictement croissante sur ]1;+∞[
et strictement croissante sur ]-∞;1[.

Les deux droites (D):x=1 et (D'):y=-2 sont les deux asymptotes de (C).

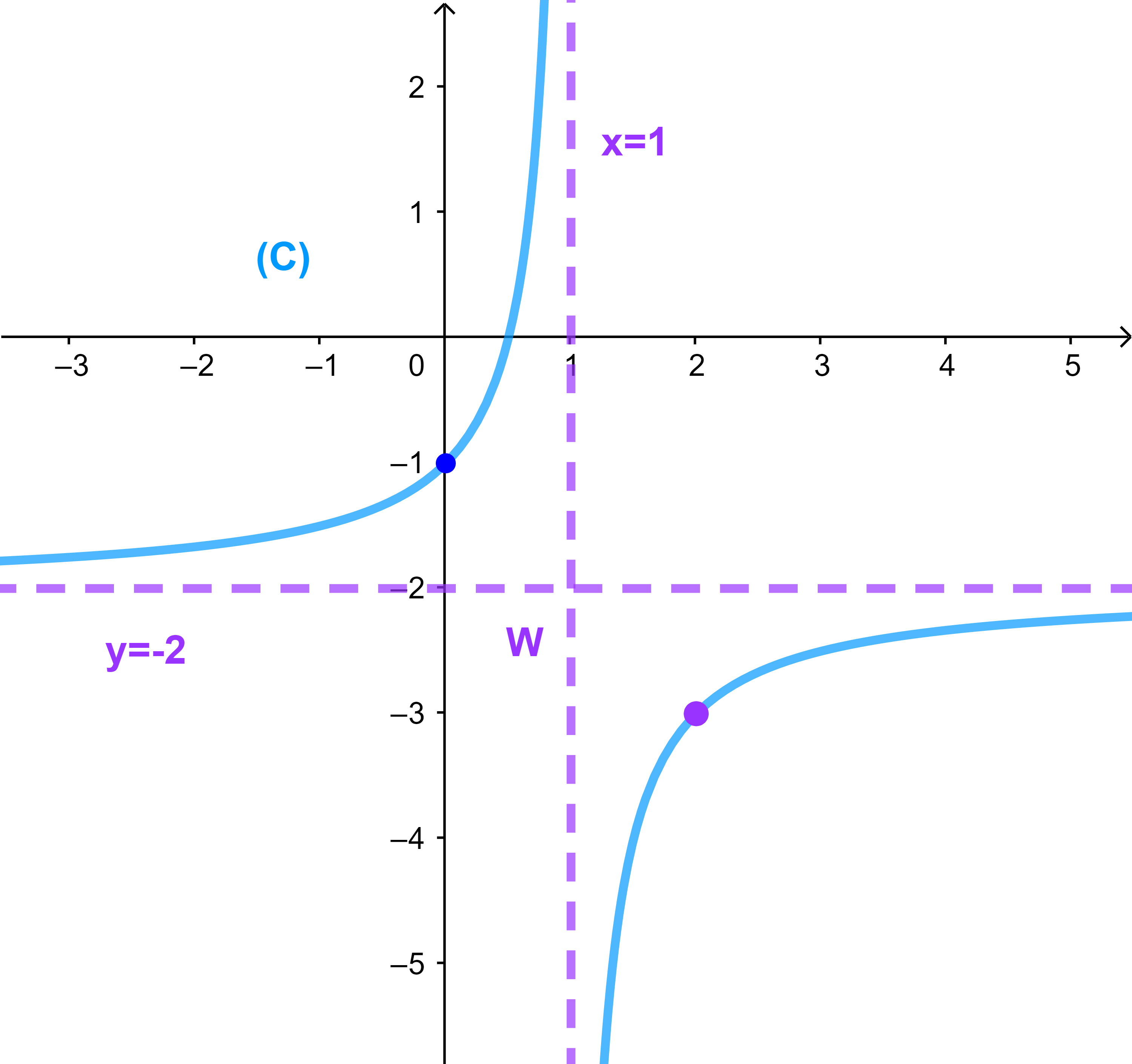
Tableau de variations

x		-∞		1		+∞
f			↗		↗

Notons qu'on peut construire la courbe sans utiliser la propriété. Il suffit de calculer des images de quelques abscisses convenables.

Exercice 2 tp

Soit f une fonction numérique définie par

f(x) =	-x+2
	x

et (C) sa courbe représentative dans un repère orthonormé (O;i^→;j^→). Déterminer une fonction g telle que f(x)=g(x)-1 et construire (C).

Correction

f est définie si x≠0 donc D=IR*=]-∞;0[∪]0;+∞[.

Soit x∈D.

f(x) =	-x	+	2	= -1 +	2
	x		x		x

On pose

g(x) =	2
	x

La courbe de g est une hyperbole de centre O(0;0).
f(x)=g(x)+(-1) donc chaque valeur de x on retranche 1 à son image par f.

(C) est donc une hyperbole de centre W(0;-1).
On sélectionne quelques images des abscisses non nulles et convenables.

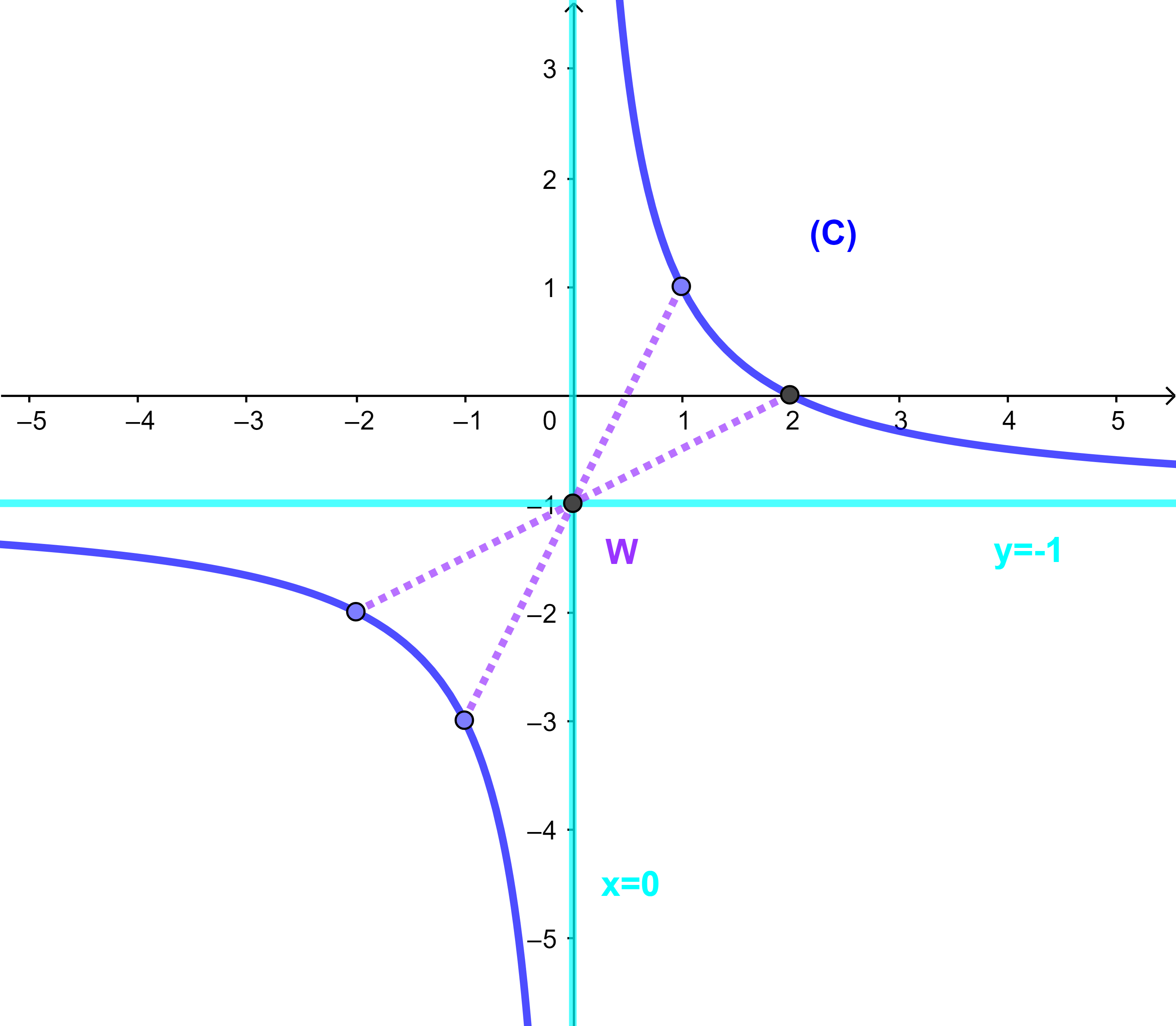
Graphiquement f est strictement décroissante
sur ]0;+∞[ et strictement décroissante
sur ]-∞;0[.

Les deux droites (D): x=0 et (D'): y=-1 sont les deux asymptotes de la courbe (C).

Tableau de variations

x		-∞		0		+∞
f			↘		↘