تمرين 1 tp

لتكن f دالة عددية معرفة كما يلي
f(x)=4x-x².
1) ادرس رتابة f
على ]-∞;2] وعلى [2;+∞[.
2) انشئ جدول تغيرات f.
3) استنتج مطرافا للدالة f.
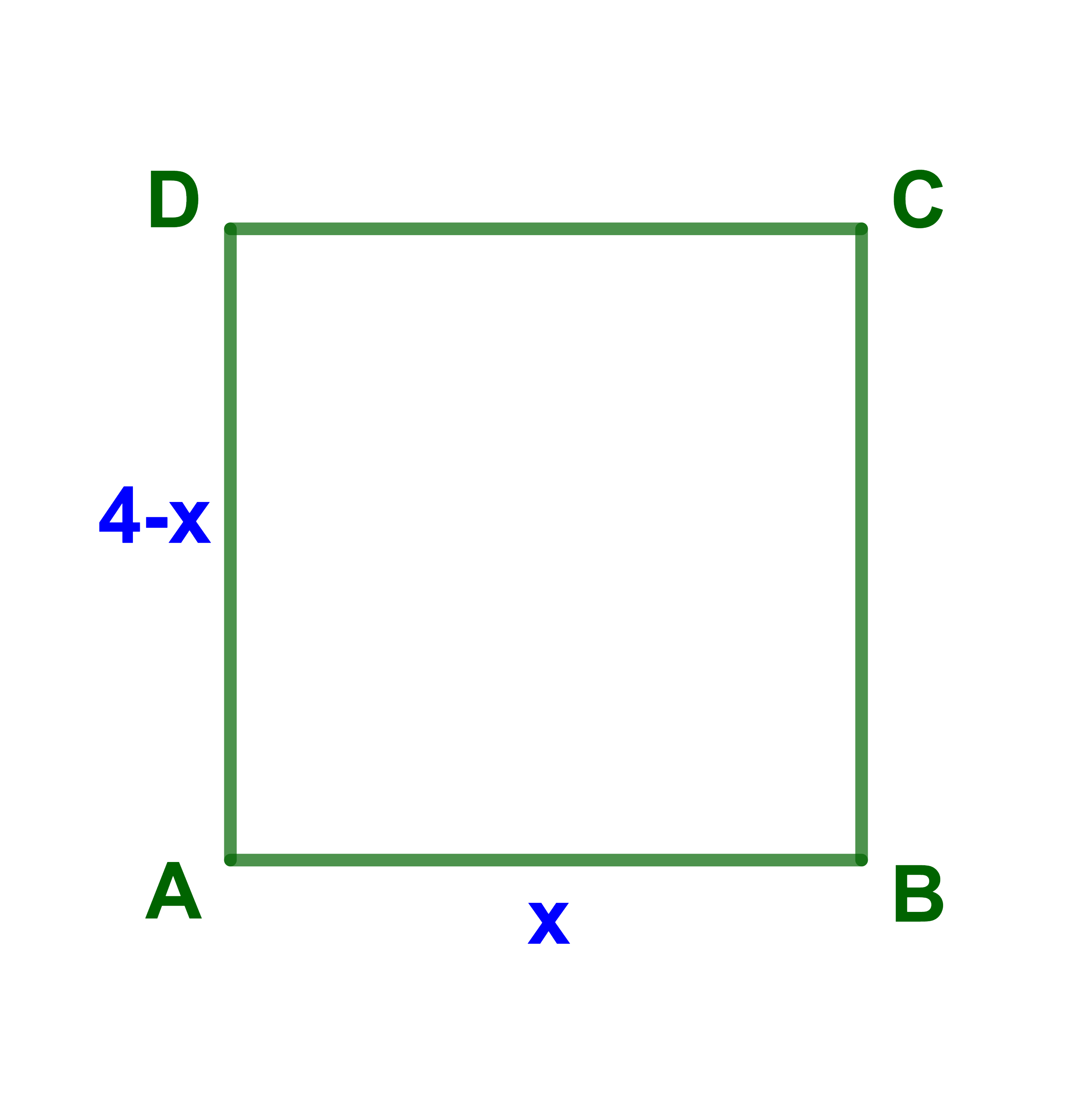
4) ليكن ABCD مستطيلا بحيث
AB=x و AD=4-x.
حدد x بحيث تكون مساحة المستطيل قصوية.

تصحيح

1) f دالة حدودية اذن D=IR.
ليكن x; y ∈IR بحيث x≠y.
f(x)-f(y)=4x-x²-(4y-y²)
=-x²+y²+4x-4y
=-(x²-y²)+4(x-y)
=-(x-y)(x+y)+4(x-y)
=(x-y)(-x-y + 4).

اذن f(x)-f(y)=(x-y)[-(x+y)+4]
ومنه فان معدل تغير T(x;y) للدالة f بين x و y

T(x;y) =	f(x) - f(y)
	x-y

يعني T(x;y)=-(x+y)+4.
1) رتابة f على I=]-∞;2].
x; y ∈I يعني x≤2 و y≤2
اذن x+y<4 (المتفاوتة قطعا لأن x و y مختلفان لايمكن أن يأخذا نفس القيمة في نفس الوقت).

x+y<4 يعني -(x+y)>-4
يعني -(x+y)+4>0
اذن T(x;y)>0 وهذا يعني أن f تزايدية قطعا
على I=]-∞;2].
2) رتابة f على J=[2;+∞[.
x; y ∈I يعني x≥2 et y≥2
اذن x+y>4
يعني -(x+y)<-4.

يعني -(x+y)+4<0
اذن T(x;y)<0 وهذا يعني f تناقصية قطعا
على J=[2;+∞[.
2) جدول التغيرات: لدينا f(2)=4.

x		-∞		2		+∞
f			↗	4	↘

3) f تزايدية قطعا
على ]-∞;2] وتناقصية قطعا
على [2;+∞[
اذن f تقبل قيمة قصوى 4 عند 2.
وبالتالي 4=f(2) مطراف للدالة f.

4) ABCD مستطيل.
مساحة المستطيل S(x)=x(4-x)
أي S(x)=4x-x².

نعتبر الدالة f
المساحة S تأخذ قيمة قصوى في a بحيث f(a) قيمة قصوى.
حسب السؤال السابق 4 هي القيمة القصوى للدالة f عند a=2
ومنه فان S تكون قصوية اذا كان x=2
بالاضافة AB=2 و AD=4-2=2
اذن ABCD مربع طول ضلعه 2.