4.3 مطارف دالة عددية

4.3.1 تعريف

لتكن f دالة عددية معرفة على مجال I بحيث (I⊂D).
كل قيمة قصوى أو قيمة دنيا للدالة f على I تسمى مطرافا للدالة f على I.

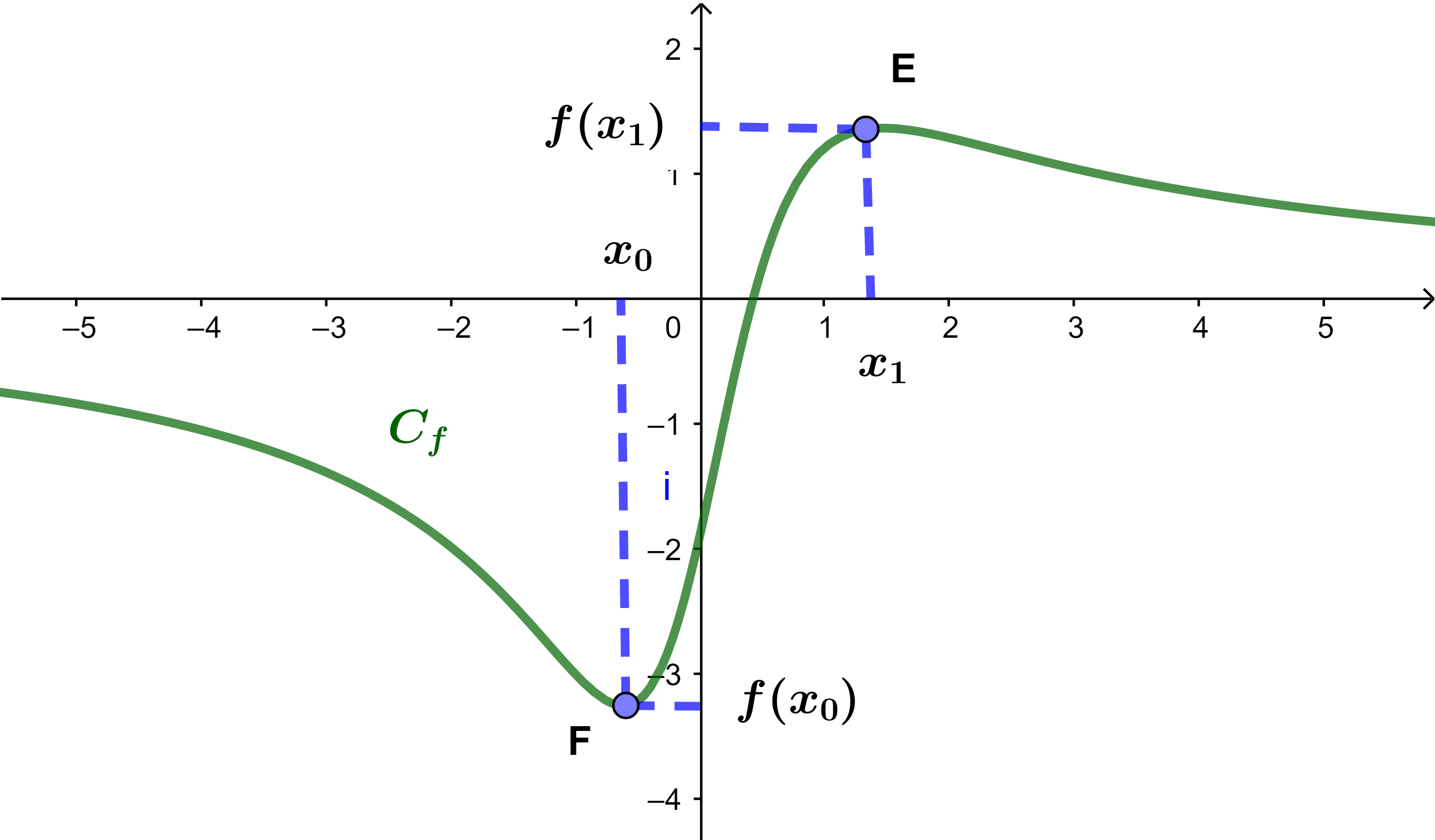
f(x₀) و f(x₁) مطرافان للدالة f.

4.3.2 مثال

لتكن f دالة عددية بحيث f(x)=2x²+4x+5.
بين أن 3 مطراف للدالة f على IR.

تصحيح
ليكن x∈IR
f(x)-3=2x²+4x+5-3
=2x²+4x+2
=2(x²+2x+1)
=2(x+1)².

2(x+1)² موجب
اذن لكل (x∈IR): f(x)≥3.
هل يوجد عنصر a في I بحيث f(a)=3 ?
f(a)=3 يعني f(a)-3=0
يعني 2(a+1)²=0 يعني a=-1
اذن 3=f(-1) قيمة دنيا للدالة f
ومنه فان 3 مطراف للدالة f.

4.4 خاصيات

لتكن f دالة عددية معرفة على مجال I=[a;b] و c∈I
1) اذا كانت f تزايدية على [a;c] وتناقصية على [c;b] فان f(c) قيمة قصوى للدالة f على I.
2) اذا كانت f تناقصية على [a;c] وتزايدية على [c;b] فان f(c) قيمة دنيا للدالة f على I.

تمرين 1 tp

لتكن f دالة عددية معرفة على مجال
I=[-3;3] بحيث f(x)=x³-12x.
1) ادرس تغيرات f
على [-3;-2] و [-2;2] و [2;3].
2) انشئ جدول تغيرات f على I.
2) استنتج مطارف الدالة f على I.

تمرين 2 tp

لتكن f دالة عددية معرفة بما يلي
f(x)=2x²-4x+7.
1) حدد العددين الحقيقيين a و b بحيث
لكل x∈IR لدينا f(x)=2(x-a)²+b.
2) استنتج b القيمة الدنيا للدالة f عند a .