Généralités sur les fonctions (7)
2.2 Fonction paire
2.2.1 Activités
Soit f une fonction numérique définie par f(x)=x².
1) Déterminer Df l'ensemble de définition de f.
2) Vérifier que Df est un domaine centré.
3) Comparer f(x) et f(-x).
Correction
1) f est un polynôme donc Df=IR.
2) L'ensemble IR est centré en 0
donc pour tout x∈Df on a (-x)∈Df.
Ainsi Df est un domaine centré en 0.
3) Soit x∈IR.
f(-x)=(-x)²=x²
donc f(-x)=f(x)
on dit alors que f est une fonction paire.
2.1.2 Définition
Soient f une fonction numérique de la variable réel x
et D son domaine de définition.
On dit que f est une fonction paire
si les deux conditions suivantes sont vérifiées
1) Pour tout x∈D on a (-x) ∈D.
2) Pour tout x∈D on a f(-x)=f(x).
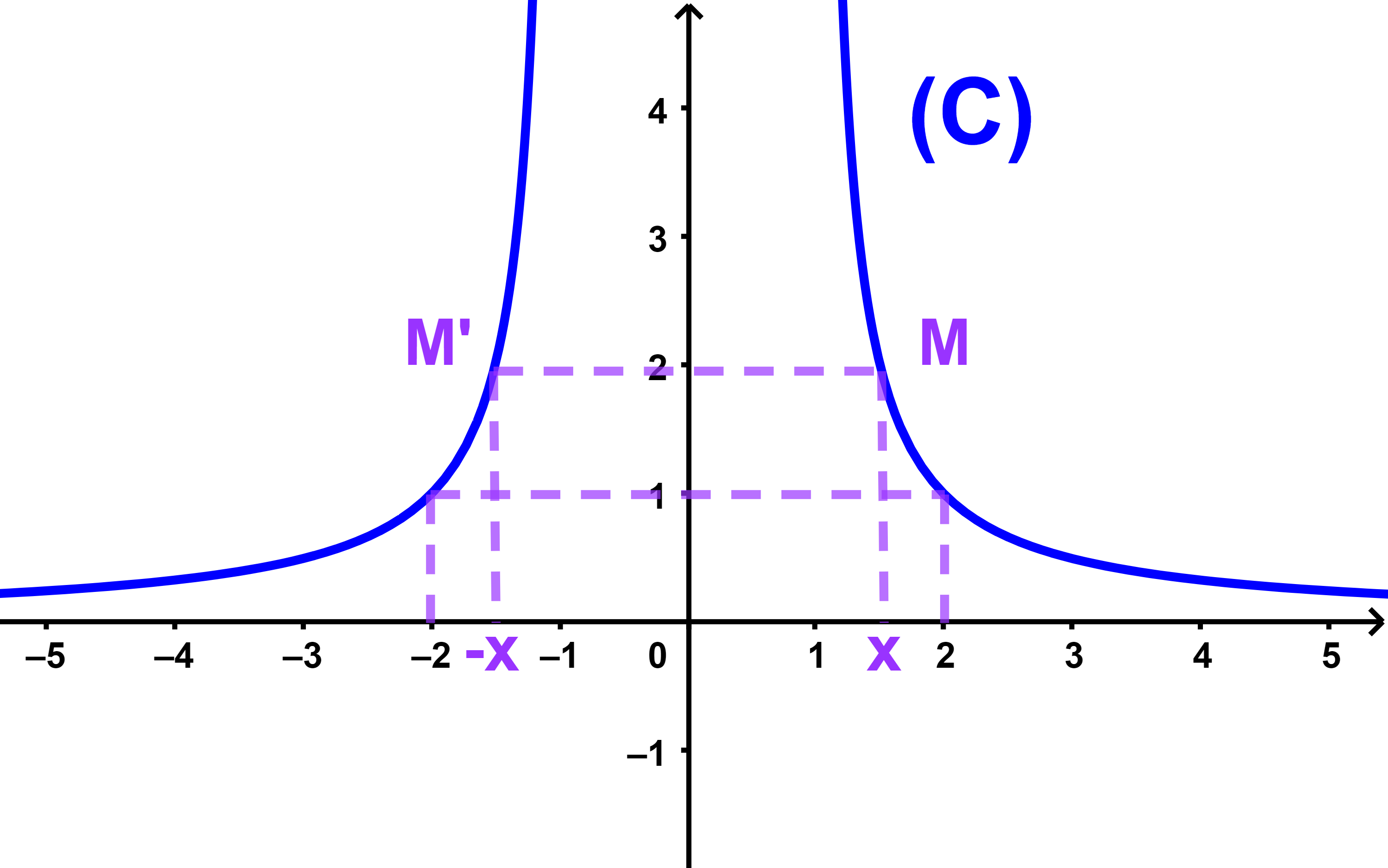
2.1.3 Interprétation graphique
Soit f une fonction paire et Cf sa courbe représentative dans un repère (O;i→;j→).
Pour tout x∈IR on a f(-x)=f(x) alors les deux points
M(x;f(x)) et M'(-x;f(x)) sont symétrique par rapport à l'axe des ordonnées.
2.1.4 Propriété
La courbe représentative d'une fonction paire est symétrique par rapport à l'axe des ordonnées.
Exercice 1 tp
Soit f une fonction numérique de la variable réel x définie par
| f(x) = | 1 |
| x²-2 |
1) Déterminer le domaine de définition de f.
2) Montrer que f est une fonction paire.
Correction
1) f est définie si son dénominateur n'est pas nul.
x²-2=0 signifie que x²=2
signifie (x=√2 ou x=-√2)
ainsi D=IR\{-√2;√2}.
2) On montre que f est paire.
L'ensemble IR est centré en 0
donc IR\{-√2;√2} est centré en 0.
Ainsi pour tout x∈D on a (-x)∈D.
Soit x∈D.
On calcule f(-x) en remplaçant x par -x.
| f(-x) = | 1 |
| (-x)²-2 | |
| = | 1 |
| x²-2 |
donc f(-x)=f(x) et par conséquent f est paire.