Exercice 1 tp

Soit f une fonction numérique définie par
f(x)=x²-4x+2 et (C) sa courbe représentative dans un repère orthonormé (O;i^→;j^→).
1) Montrer que pour tout x∈IR
f(4-x)=f(x).
2) (D) est une droite d'équation x=2
(a) On considère un point M(x;f(x)) de la courbe de f et M'(x';y') un point du plan.
Déterminer x' et y' en fonction de x et y de façon que (D) soit médiatrice du segment [MM'].

(b) Montrer que M'∈(C).
(c) Que peut on dire de la droite (D) par rapport à (C) ?

Exercice 2 tp

Soit f une fonction numérique définie par

f(x) =	1
	x-1

et (C) sa courbe représentative dans un repère orthonormé (O;i^→;j^→).
1) Déterminer D le domaine de définition de f.
2) Montrer que pour tout x∈D on a f(2-x)=-f(x).

3) Soit I(1;0) un point du plan
(q1) on considère M(x;f(x)) un point de la courbe de f et M'(x';y') un point du plan.
Déterminer x' et y' en fonction de x et y tel que I soit milieu du segment [MM'].
(q2) Montrer que M' est un point de la courbe (C) de f
(q3) Que peut on dire du point I par rapport à (C) ?

Exercice 3 tp

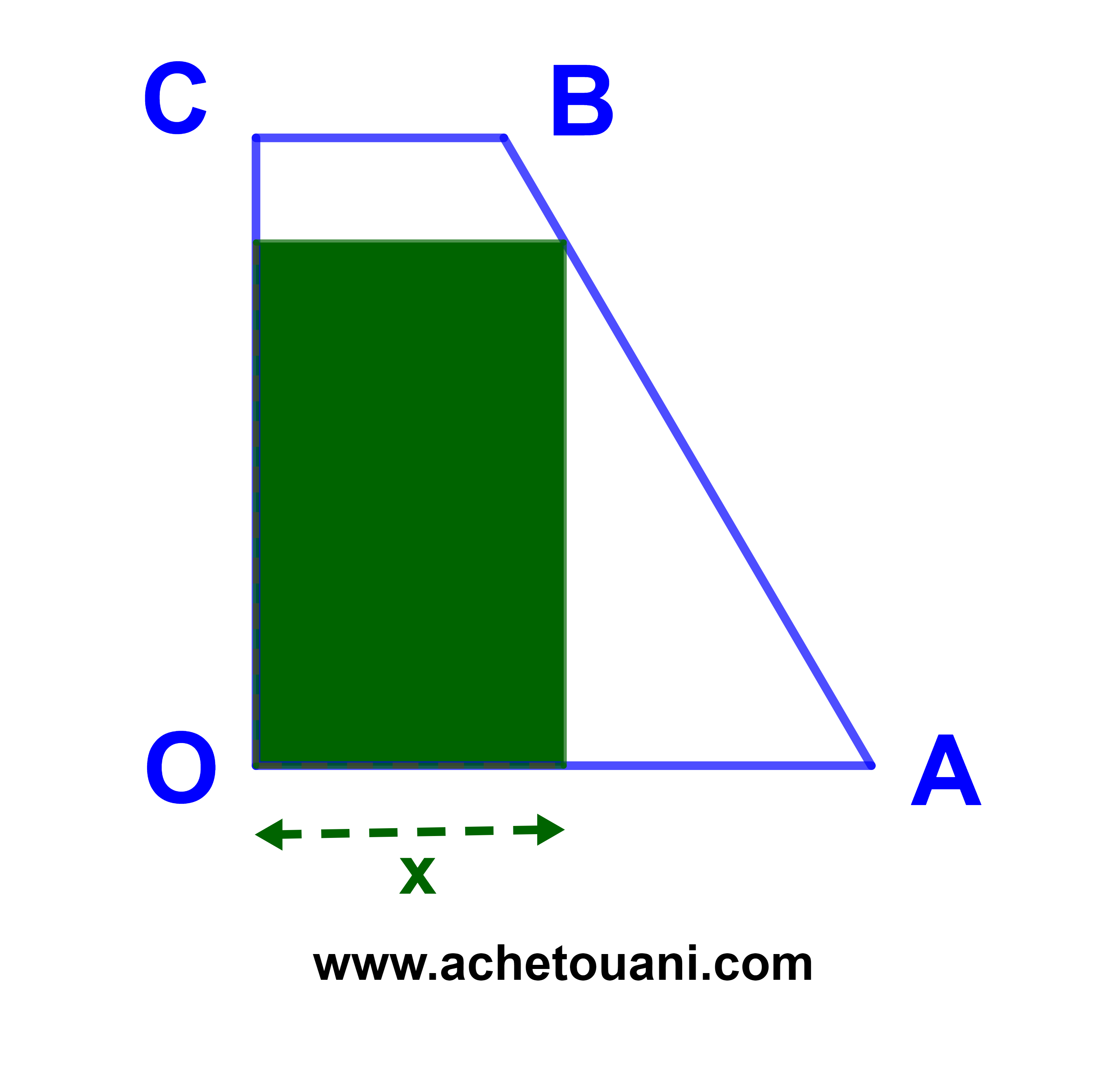
Un terrain OABC en forme de trapèze rectangle en O et C.
OA=10m ; OC=10,2m et CB=4m (voir la figure)
son propriétaire a souhaité en exploiter une parite de la forme rectangulaire et sa superficie au maximum.
Déterminer sa longueur et sa largeur.