2- المستقيم العددي والمجالات

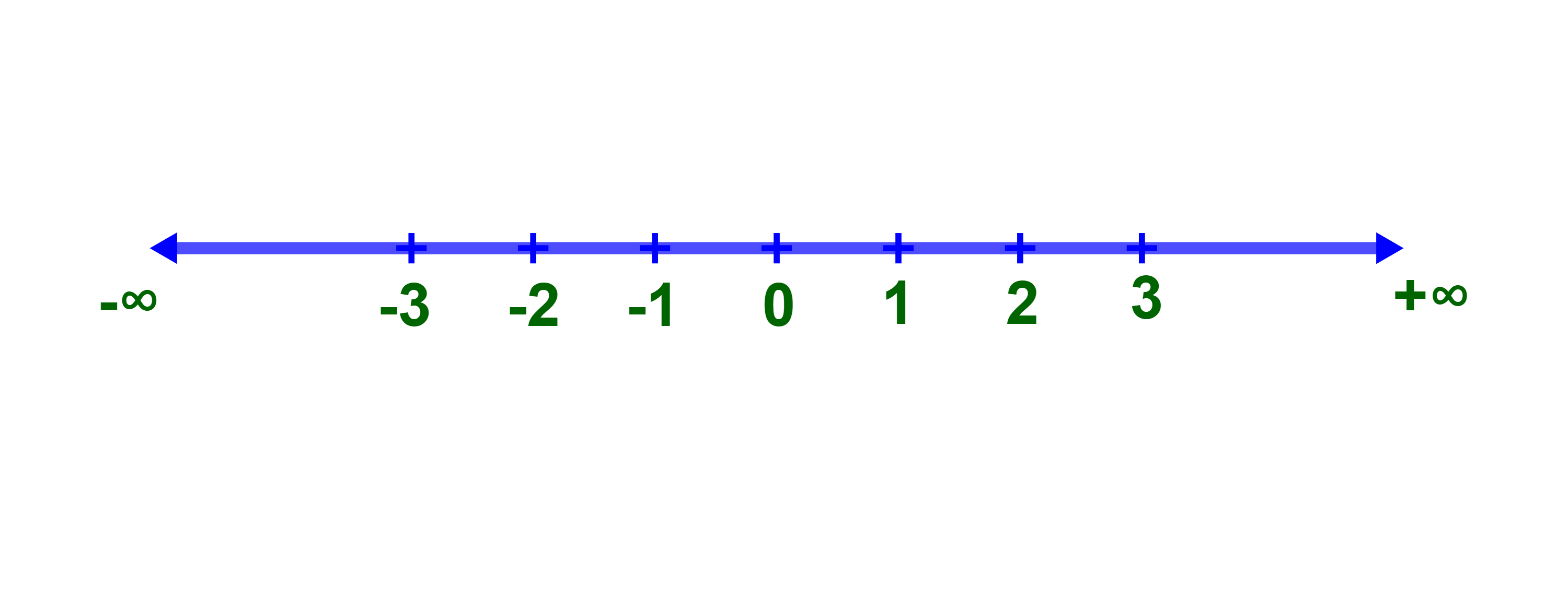
2.1 المستقيم العددي

2.1.1 انشطة

1) انشئ النقط A و B و C على محور متدرج (OI) افاصيلها على التوالي 4 و -5 و - 2.
2) حدد قطعة تحتوي على النقطة C ولا تحتوي على النقطة A.

3) احسب المسافات OA و OB و OC و AB و AC و BC

للتذكير
مسافة نقطتين على محور متدرج تساوي فرق بين أكبر افصول وأصغر افصول.

2.1.2 تعريف

ليكن (D) محورا متدرجا.
كل نقطة M من المحور (D) تمثل عدد حقيقي x
وعكسيا كل عدد حقيقي x هو افصول لنقطة M من المحور (D).
نقول اذن ℝ هي المستقيم العددي.

2.2 المجالات

2.2.1 انشطة

1) في مقابلة لكرة القدم تلعب شوطين.
مدة كل شوط 45 دقيقة وتفصلها قترة استراحة لمدة 15 دقيقة. اذن توجد ثلاث مراحل زمنية لهذه المقابلة :)

المرحلة الاولى تبدأ من الدقيقة 0 الى الدقيقة 45. هذه المرحلة الزمنية تسمى مجالا محدودا ونرمز له ب ]0;45].
2) توجد مدة صلاحية لاستهلاك مواد غذائية
هذه المدة تحدد مجالا.

2.2.2 المجالات المحدودة

ليكن a و b عددين حقيقيين حيث a<b.
مجموعة الأعداد الحقيقية المحصورة بين a و b تسمى مجالا طرفاه a و b ويوجد اربعة اصناف.
1) [a;b] يسمى مجالا محدودا مغلقا.
2) [a;b[ يسمى مجالا محدودا مفتوحا على اليمين.
3) ]a;b] يسمى مجالا محدودا مفتوحا على اليسار.
4) ]a;b[ يسمى مجالا مفتوحا ومحدودا.

2.2.3 المجالات غير المحدودة

1) ليكن a عددا حقيقيا.
مجموعة الأعداد الحقيقية التي أكبر من أو تساوي a هي مجال غير محدود ونرمز له ب ]a;+∞[={x∈IR/x≥a}.

مثال I=[3;+∞[
-8∉I ; 0∉I ; √(7)∉I 3∈I ; ...

2) ليكن a عددا حقيقيا. مجموعة الأعداد الحقيقية التي أصغر من أو تساوي a هي مجال غير محدود ونرمز له ب ]-∞;a]={x∈IR/x≤a}.

مثال I= ]-∞;5]
0∈I ; -18∈I ; √(30)∉I..

3) المجموعة ℝ هي مجال غير محدود
ℝ=]-∞;+∞[.

ملاحظة
الرمز ∞ يعني ما لا نهاية والرمز \ يعني باستثناء.
ℝ⁺=[0;+∞[ ; ℝ^-=]-∞,0].
ℝ^*=ℝ\{0}.
∅={} هي المجموعة الفارغة.