Ordre dans IR (3)
2.2.4 Intervalle centré
Définition
Soit I un intervalle ou un domaine.
On dit que I est centré en 0 ou symétrique si la condition suivante est vérifiée
Si x∈I alors (-x)∈I.
Exemples
I=[-4;4] est un intervalle centré en 0.
J=]-5;5] n'est pas un intervalle centré en 0 car 5∈J mais (-5)∉J.
D=]-4;-2]∪[2;4[ est un domaine centré en 0.
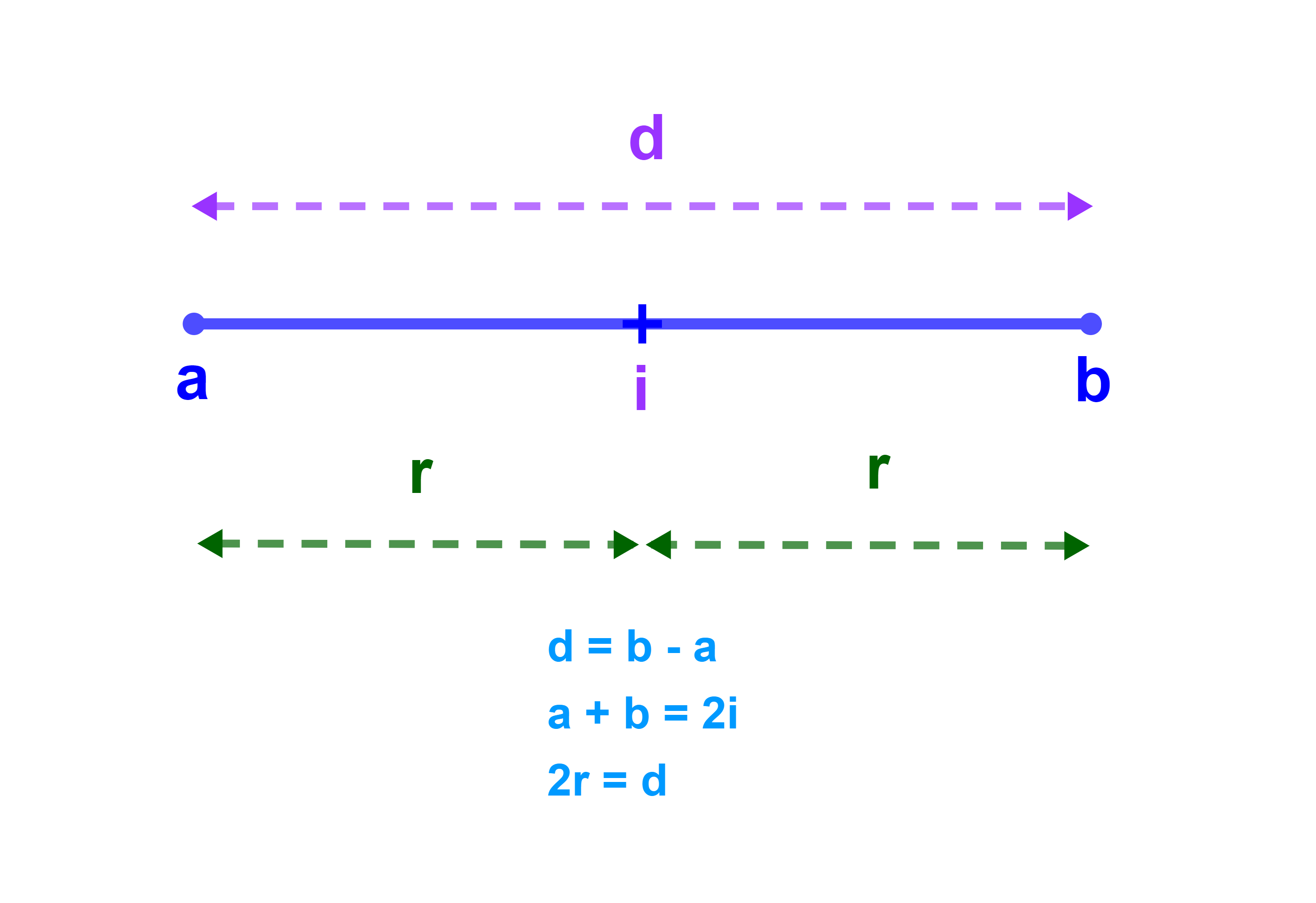
2.2.5 Centre et rayon d'un intervalle borné
Définition
Soit I un intervalle borné d'extrémités a et b tels que a<b.
On dit que α est le centre de I si α-a = b-α.
En d'autre terme α est un centre de I si a+b=2α
Notons que le nombre r=α-a= b-α est le rayon de l'intervalle I.
Résultat
Soit I un intervalle de centre α et de rayon r
| α = | a+b | et | r = | b-a |
| 2 | 2 |
Exercice 1 tp
Soit I=[2;12] un intervalle.
Déterminer le centre et le rayon de I.
Correction
On désigne par i au centre et par r au rayon.
| i = | 2+12 | = 7 |
| 2 | ||
| r = | 12-2 | = 5 |
| 2 |
donc I est un intervalle de centre 7 et de rayon 5.
Exercice 2 tp
Déterminer tous les intervalles de centre 3 et de rayon 1
Correction
Soit I un intervalle de centre 3 et de rayon 1.
donc ses extrémités sont 1+3=4 et 3-1=2.
Donc tous les intervalles de centre 3 et de rayon 1 sont
| [2 ; 4] | ]2 ; 4[ | |
| [2 ; 4[ | ]2 ; 4] |