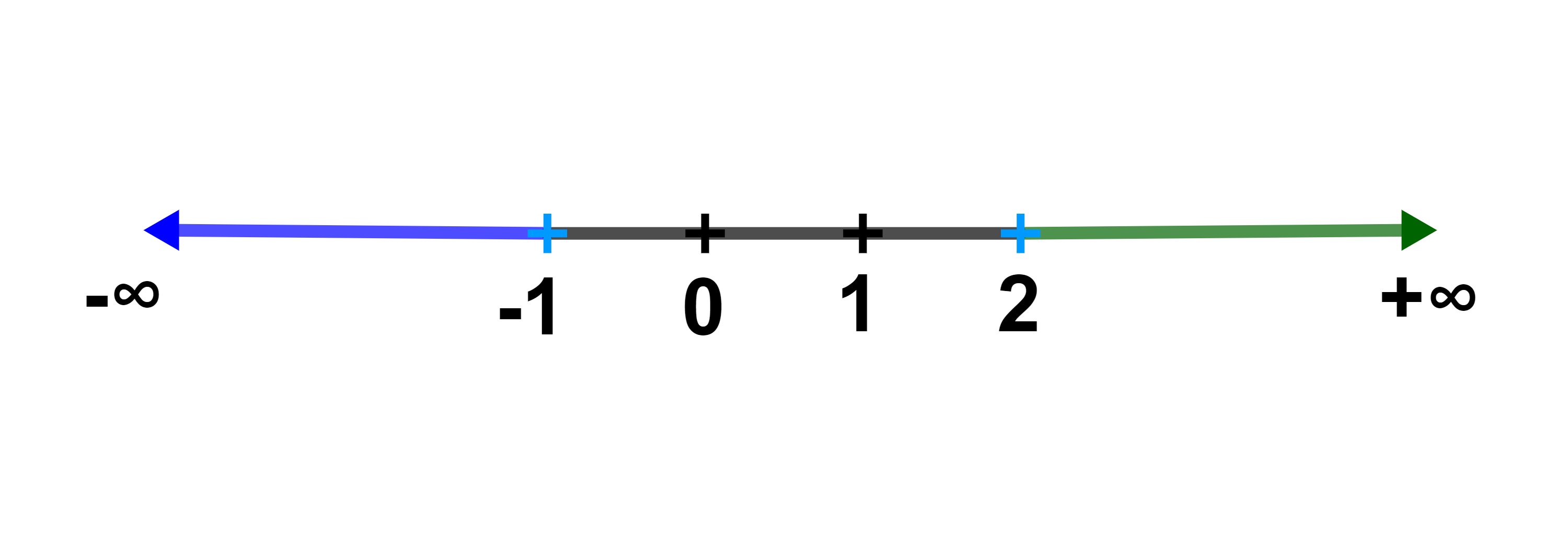Exercice 1 tp

1) Soit x∈IR.
A quel intervalle appartient x tel que
2x+3≤7 ?
2) Soit x∈IR.
A quel intervalle appartient x tel que
-3x+4≥13 ?

Correction

1) Soit x∈IR.
2x+3≤7 signifie 2x≤7-3
signifie 2x≤4 signifie x≤2
donc x∈]-∞ ; 2].
-∞ --- 2 --- → +∞

2) Soit x∈IR.
-3x+4 ≥ 12 signifie -3x≥13-4
signifie -3x≥9 signifie 3x≤-9
donc x≤-3 ainsi x∈]-∞;-3].
-∞ --- -3 --- → +∞

Exercice 2 tp

Soit D un ensemble des nombre réel à l'excéption de 1.
Ecrire D avec des intervalles ou leur union.

Correction

On a D=IR\{1}.
x∈D signifie x≠1
signifie (x>1) ou (x<1)
x>1 signifie x∈ I=]1;+∞[
x<1 signifie x∈ J=]-∞;1[.

On a donc x∈D signifie x appartient à l'union de deux intervalles I et J
ainsi D=]-∞;1[∪]1;+∞[.

Exercice 3 tp

Soit D un ensemble des nombres réels à l'excéption de -1 et 2.
Ecrire D avec des intervalles ou leur union.

Correction

D=IR\{-1;2}
x∈D sigbifie (x≠-1) ou (x≠2).
Les deux points d'abscisses respectives (-1) et 2 sur la droite numérique déterminent trois parties de l'axe.

On a donc x∈D
signifie (x<-1) ou (-1<x<2) ou (x>2).
1) x<-1 signifie x∈I=]-∞;-1 [
2) -1<x<2 signifie x∈J=]-1;2[
3)x>2 signifie x∈K=]2;+∞[.

donc x∈D signifie que x appartient à l'union des intervalles I ; J et K
ainsi D=]-∞;-1[∪]-1;2[∪]2;+∞[.