تمرين 1 tp

x∈IR. الى اي مجال ينتمي العدد x بحيث 2x+3 ≤ 7

تصحيح

2x+3 ≤ 7 يعني 2x≤7-3
اي 2x ≤ 4 اذن x ≤ 2
ومنه فان x∈]-∞;2]
-∞ --- 2 --- → +∞

تمرين 2 tp

x∈IR الى اي مجال ينتمي العدد x بحيث -3x+4≥13

تصحيح

-3x+4≥12 يعني -3x≥13-4
اي -3x≥9 اي 3x≤-9
اذن x≤-3
ومنه فان x∈]-∞;-3]
-∞ --- -3 --- → +∞

تمرين 3 tp

ليكن x∈IR\{-2} و A عددا حقيقيا معرف كما يلي

A =	1
	x+2

اذا كان 2 < A < 4
الى اي مجال ينتمي العدد x

تصحيح

بما ان A محصور بين عددين موجبين قطعا فهو موجب قطعا ومنه فان x+2 موجب قطعا.

2 <	1	< 4
	x+2
1	< x+2 <	1
4		2
1	- 2 < x < -2 +	1
4		2
- 7	< x <	- 3
4		2

x∈]	- 7	;	- 3	[ وبالتالي
	4		2

تمرين 4 tp

ليكن I=[2;12] مجالا. حدد مركز وشعاع I.

تصحيح

نرمز ب i للمركز و ب r للشعاع

{	i =	2+12	= 7
		2
	r =	12-2	= 5
		2

اذن 7 مركز المجال I و 5 شعاعه

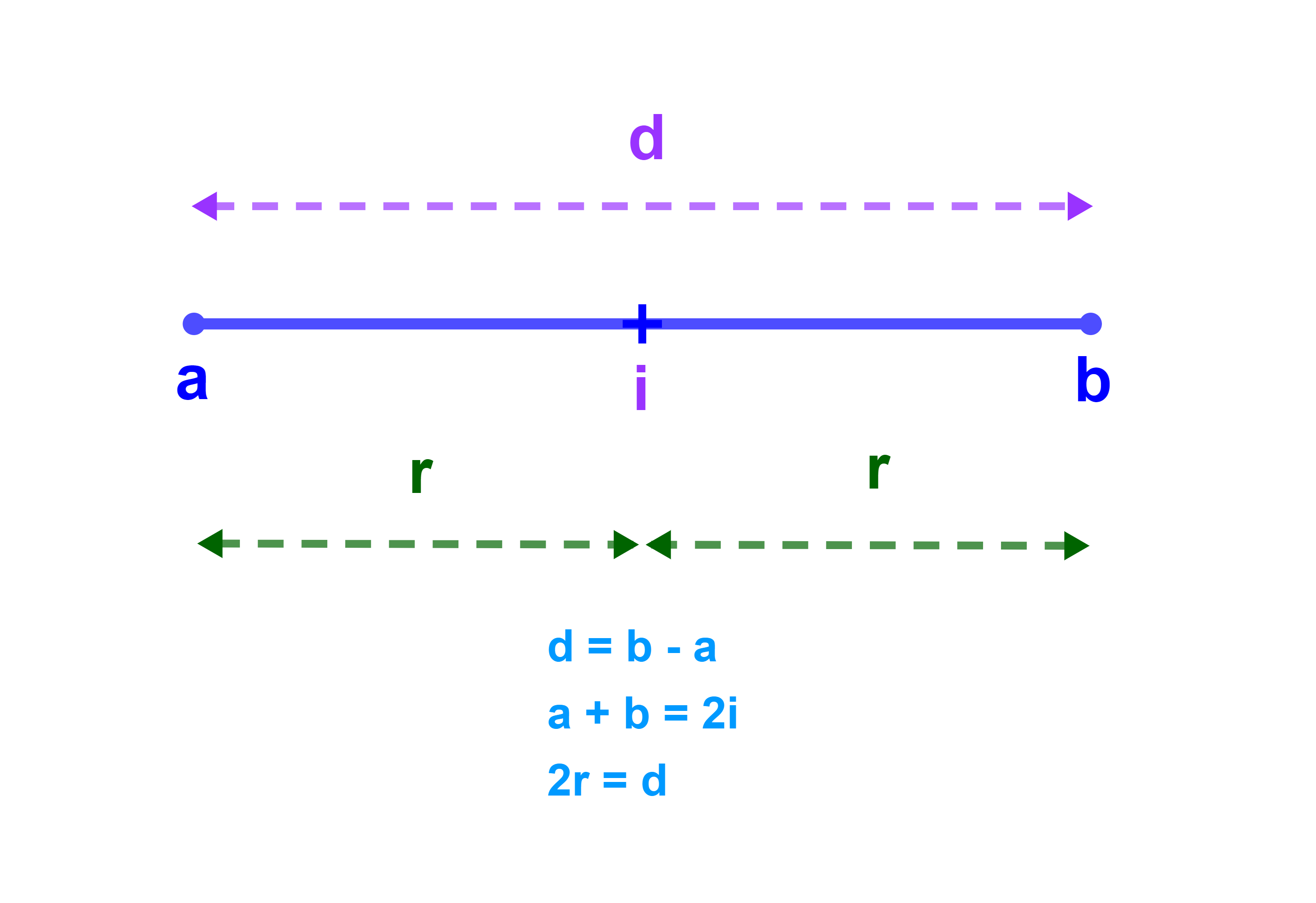
تمرين 5 tp

ليكن I مجالا مركزه 10 وشعاعه 12. حدد I
2) ليكن J=]5;b[ مجالا شعاعاه 7. حدد b والمركز i.

تصحيح

1) طريقة (1) لدينا b-a=d=2.12=24
a+b=2i=2.10=20. نحل النظمة التالية

{	-a + b = 24
	a + b = 20

نجمع طرفي المعادلتين طرفا طرفا فنحصل 2b=24+20=44 اذن b=22.

نعوض قيمة b في احدى المعادلتين
a+22=20 اذن a=-2 ومنه فان I=[-2;22].
طريقة (2) a=i-r=10-12=-2
و b=i+r=10+12=22.
2) لدينا J=]5;b[ و r=7 اذن b-5=2r=14 ومنه فان b=19
ولدينا a+b=2i أي 5+19=2i
أي 2i=24 ومنه فان i=24÷2=12.