Exercice 1 tp

1) Soit x∈IR tel que |x-1| < 1
Montrer que x∈]0; 2[
2) Soit x∈IR tel que |x+1| > 1
Montrer que x∈]-∞;-2[∪]0;+∞[.

Correction

Rappel
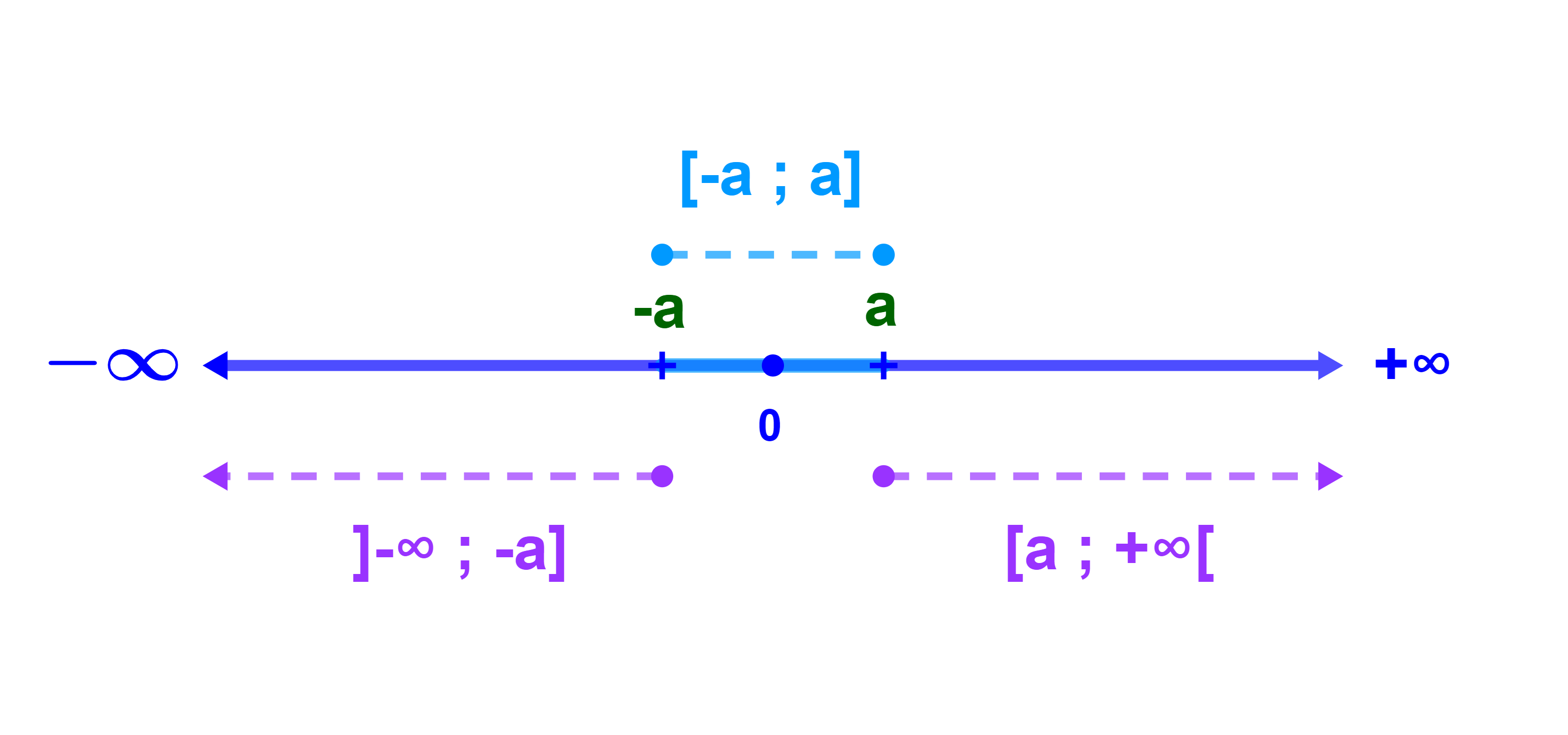
(a) |x|≤k signifie - k≤x≤k
(b) |x|≥k signifie x≤-k ou x≥k

1) |x-1|<1 signifie -1<x-1<1
signifie -1+1<x<1+1
signifie 0<x<2
ainsi x∈]0;2[.
2) |x+1|>1 signifie (x+1<-1 ou x+1>1)
signifie (x<-2 ou x>0)
signifie x∈]-∞;-2[∪]0;+∞[.

Exercice 2 tp

Soit x∈IR.
Montrer que si |x-1|<0,1
alors |x+1|<2,1.

Correction

|x-1|<0,1 signifie -0,1<x-1<0,1
signifie -0,1+1<x<0,1+1
signifie 0,9<x<1,1
signifie 0,9+1<x+1<1,1+1
signifie 1,9<x+1<2,1
et puisque 1,9>- 2,1
alors - 2,1<x+1<2,1
et cela signifie que |x+1|<2,1.

Exercice 3 tp

Soit x∈IR.
Montrer que si |x-2|<0,5
alors |x²-4|<2,25.

Correction

|x²-4|=|x-2||x+2|
|x-2|<0,5 signifie -0,5<x-2<0,5
signifie -0,5+2<x<0,5+2
signifie 1,5<x<2,5

Signifie 1,5+2<x+2<2,5+2
signifie 3,5<x+2<4,5.
Puisque 3,5>-4,5
alors - 4,5<x+2<4,5
et cela signifie que |x+2|<4,5 donc
|x²-4|=|x-2||x+2|<0,5 × 4,5
alors|x²-4|<2,25.

Exercice 4 tp

Soit x∈IR.
Montrer que si |x+2|<0,2
alors |4x+5|<3,3.