1- الاسقاط

1- الاسقاط على مستقيم

1.1.1 تعريف

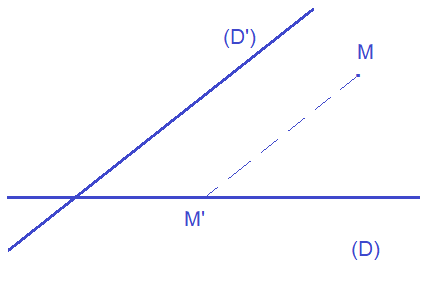
ليكن (D) و (Δ) مستقيمين متقاطعين في النقطة O و M نقطة من المستوى.
يمر من M مستقيم اتجاهه (Δ) ويقطع (D) في نقطة واحدة M' تسمى مسقط النقطة M على المستقيم (D) في اتجاه المستقيم (Δ).

ملاحظة العلاقة التي تربط كل نقطة M من المستوى بمسقطها M' على (D) في اتجاه (Δ) تسمى الاسقاط على (D) في اتجاه (Δ) ونرمز له ب p.

p(M)=M' يعني M' مسقط M.

1.1.2 نتائج

ليكن (D) و (Δ) مستقيمين متقاطعين في نقطة O. نعتبر الاسقاط على (D) في اتجاه (Δ).
1) كل نقطة من (D) مسقطها نفسها.
نقول ان المستقيم (D) صامد بالاسقاط.

2) نقط المستقيم (Δ) لها مسقط واحد هو النقطة O اذن الاسقاط لا يحافظ على المسافة.
3) كل نقطة من (D) هي مسقط ما لانهاية من النقط.

1.2 الاسقاط العمودي

تعريف

ليكن (D) و (Δ) مستقيمين متقاطعين في نقطة O. يكون الاسقاط عموديا على (D) اذا كان الاتجاه (Δ) عموديا على (D)
((D)⊥(Δ)).

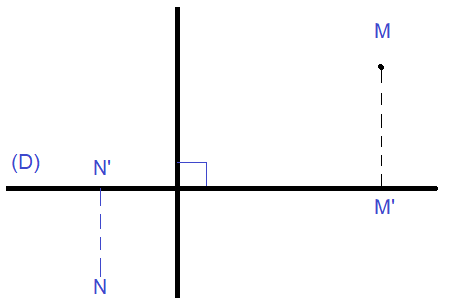
ملاحظة
ليس من الضروري تعيين الاتجاه عنما يتعلق الأمر بالاسقاط العمودي.

تمرين 1 tp

ليكن ABCD متوازي أضلاع مركزه O.
انشئ مسقط كل من النقط A و B و C و D و O على (CD) في اتجاه (AC).