1- Projection

1- La projection sur une droite

1.1.1 Définition

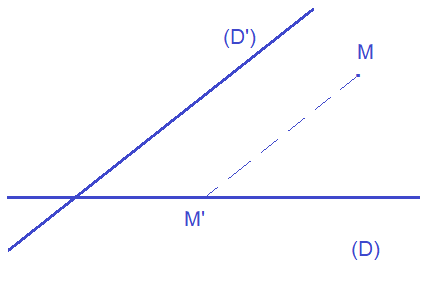
Soient (D) et (Δ) deux droites sécantes au point O. On considère un point M du plan.
Elle passe par M une droite de direction (Δ) et coupe (D) en un seul point M'.
Le point M' est appelé Projeté de M sur (D) selon la direction (Δ).

Notons que la relation qui lie chaque point M du plan par sa projection M' sur la droite (D) selon la direction (Δ) est appelée la projection sur (D) selon la direction (Δ) et est notée p.

p(M)=M' signifie que M' est le projeté de M.

1.1.2 Résultats

Soient (D) et (Δ) deux droites sécantes au point O. On considère la projection sur (D) selon la direction (Δ).
1) Le projeté de chaque point de (D) est lui même.
Ainsi la droite (D) est invariante par la projection.

2) Les points de la droite (Δ) se projettent au point O et donc la projection ne conserve pas la distance.
3) Chaque point de la droite (D) est le projeté d'une infinité des points.

1.2 Projection orthogonale

Définition

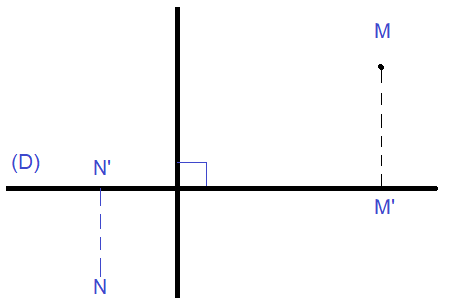
Soit p la projection sur la droite (D) selon la direction (Δ).
Si la direction (Δ) est perpendiculaire à (D) alors la projection p est appelé projection orthogonale sur (D).

Remarque
Unitile de signaler la direction quand on parle de la projection orthogonale sur une droite.

Exercice t1 tp

Soit ABCD un parallélogramme de centre O.
Tracer le projeté de chacun des points
A ; B ; C ; D et O sur (CD) selon la direction (AC).