الاسقاط (3)
2- تطبيقات
2.1 مبرهنة طاليس
2.1.1 مبرهنة طاليس المباشرة
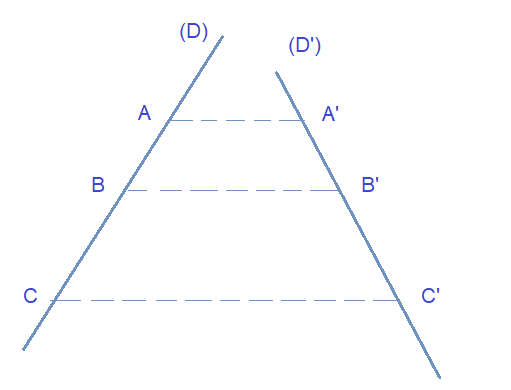
ليكن (D) و (Δ) مستقيمين متقاطعين في النقطة O و
A و B و C ثلاث نقط مستقيمية
اذا كانت A' و B' و C' هي مساقطها على (D) في اتجاه (Δ) على التوالي فان
| AB | = | A'B' |
| AC | A'C' |
2.1.2 مبرهنة طاليس العكسية
ليكن (D) و (Δ) مستقيمين متقاطعين في النقطة O
A و B نقطتين و A' و B' مسقطيهما على (D) في اتجاه (Δ) على التوالي.
اذا كانت C∈(AB) و C'∈(A'B') (C' تتبع ترتيب C بالنسبة للنقط الاخرى )
واذا كان
| AB | = | A'B' |
| AC | A'C' |
فان النقطة C' هي مسقط النقطة C.
2.2 حالة مثلث
2.2.1 مبرهنة 1
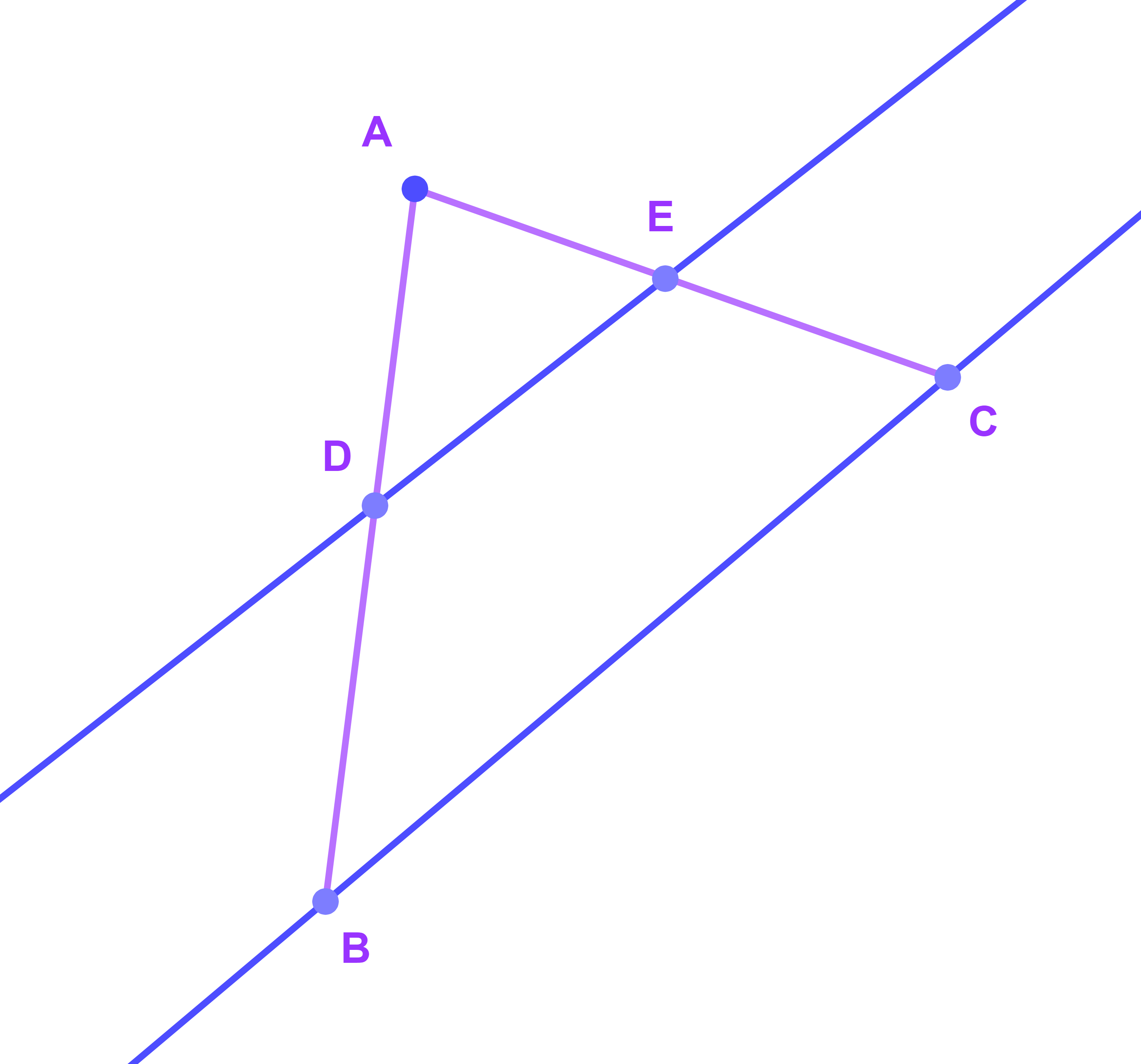
ليكن ABC مثلثا
D∈[AB] و E∈[AC].
اذا كان (MN)||(BC) فان
| AD | = | AE | = | DE |
| AB | AC | BC |
2.2.2 مبرهنة 2
ليكن ABC مثلثا
(D∈[AB] و E∈[AC]) أو (A∈[BD] و A∈[CE]).
اذا كان
| AD | = | AE | = | DE |
| AB | AC | BC |
فان (DE)||(BC).
3) اذا كانت D منتصف القطعة [AB]
و E منتصف القطعة [AC]
فان (DE)||(BC).
تمرين 1 tp
ليكن ABC مثلثا.
هل (MN)||(BC) علما أن AB=5 و AC=10 و AM=2 و AN=4 و M∈[AB] و N∈[AC] ؟
تمرين 2 tp
ليكن ABC مثلثا.
هل (MN)||(BC) علما أن AB=8 و AC=9 و AM=4 و AN=5 و A∈[NC] و N∈[MB] ؟
تمرين 3 tp
ليكن ABC مثلثا.
نعتبر أن (BC)||(MN) و AN=5 و AC=4 و AB=5 و MN=7.
احسب BC و AM.