La projection (3)
2- Applications
2.1 Théorèmes de Thalès
2.1.1 Théorème de Thalès direct
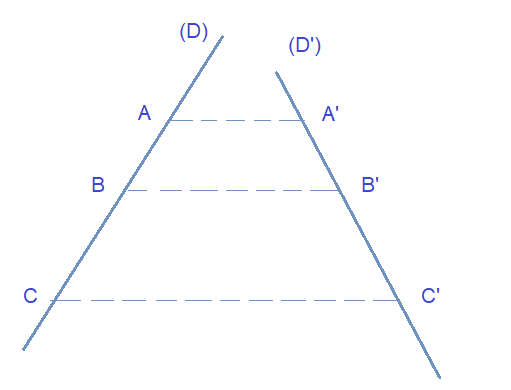
Soient (D) et (Δ) deux droites sécantes au point O.
A; B et C sont trois points alignés. Si A'; B' et C' sont leurs projetés sur la droite (D) selon la direction (Δ) alors
| AB | = | A'B' |
| AC | A'C' |
2.1.2 Réciproque du théorème de Thalès
Soient A; B deux points et A'; B' leurs projetés sur une droite (D) selon une direction (Δ).
Si C∈(AB) ; C'∈(A'B') (C' suit l'ordre de C par rapport aux autres points)
et si
| AB | = | A'B' |
| AC | A'C' |
alors le point C' est le projeté du point C.
2.2 Cas d'un triangle
2.2.1 Théorème 1
Soient ABC est un triangle
D∈[AB] et E∈[AC].
Si (MN)||(BC) alors
| AD | = | AE | = | DE |
| AB | AC | BC |
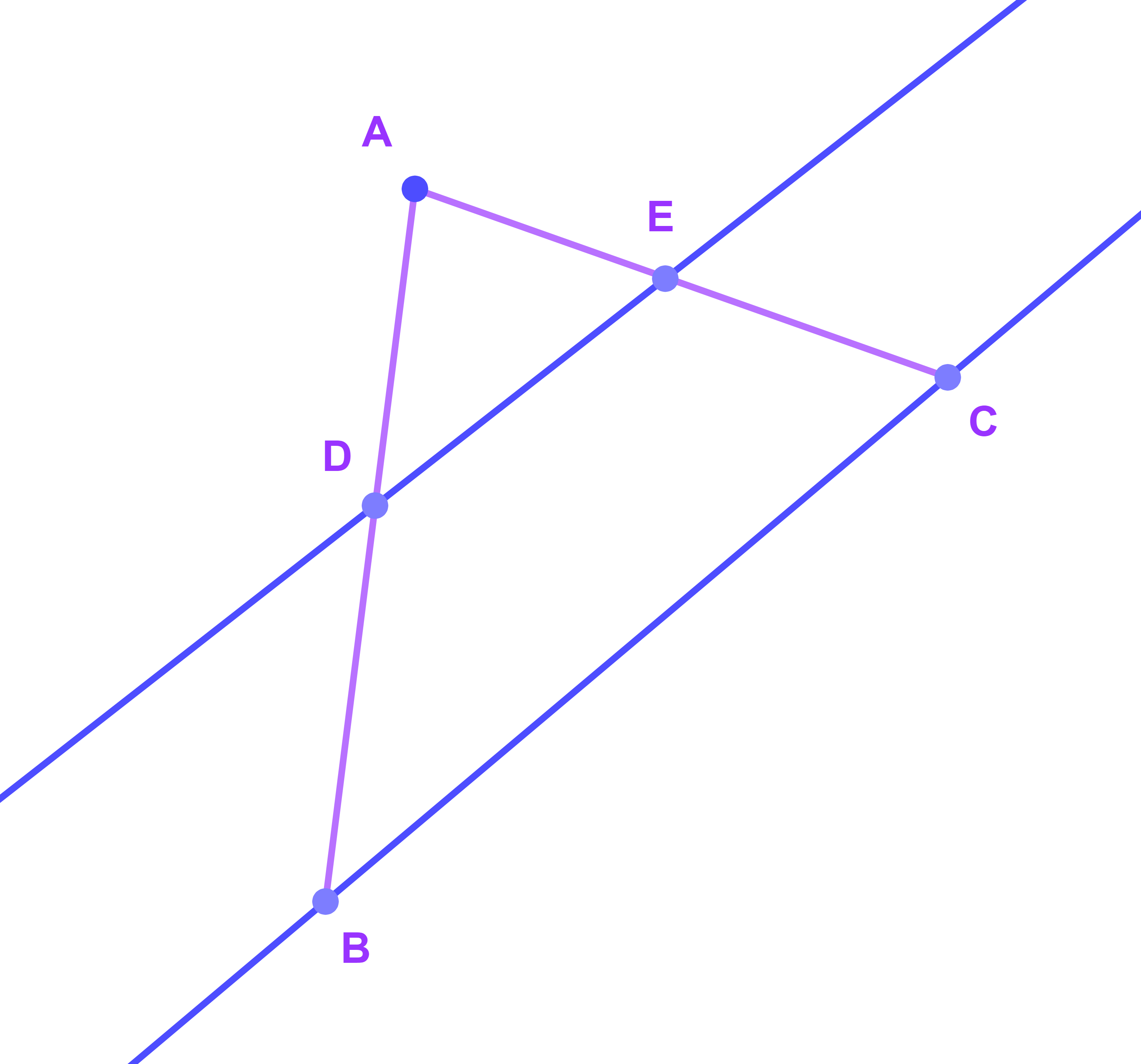
2.2.2 Théorème 2
Soient ABC un triangle
(D∈[AB] et E∈[AC]) ou (A∈[BD] et A∈[CE]).
Si
| AD | = | AE | = | DE | |
| AB | AC | BC |
alors (DE)||(BC).
3) Si D est le milieu du segment [AB]
et E est le milieu du segment [AC]
alors (DE)||(BC).
Exercice 1 tp
Soit ABC un triangle.
Est ce que (MN)||(BC)? sachant que AB=5 ; AC=10 ; AM=2 ; AN=4 ; M∈[AB] et N∈[AC].
Exercice 2 tp
Soit ABC un triangle.
Est ce que (MN)||(BC)? sachant que AB=8 ; AC=9 ; AM=4 ; AN=5 ; A∈[NC] et N∈[MB].
Exercice 3 tp
Soit ABC un triangle.
On donne (BC)||(MN) ; AN=5 ; AC=4 ; AB=5 et MN=7.
Calculer BC et AM.