الجداء السلمي في المستوى (1)
الجداء السلمي لمتجهتين
1.1 تعريف وخاصية
1.1.1 أنشطة
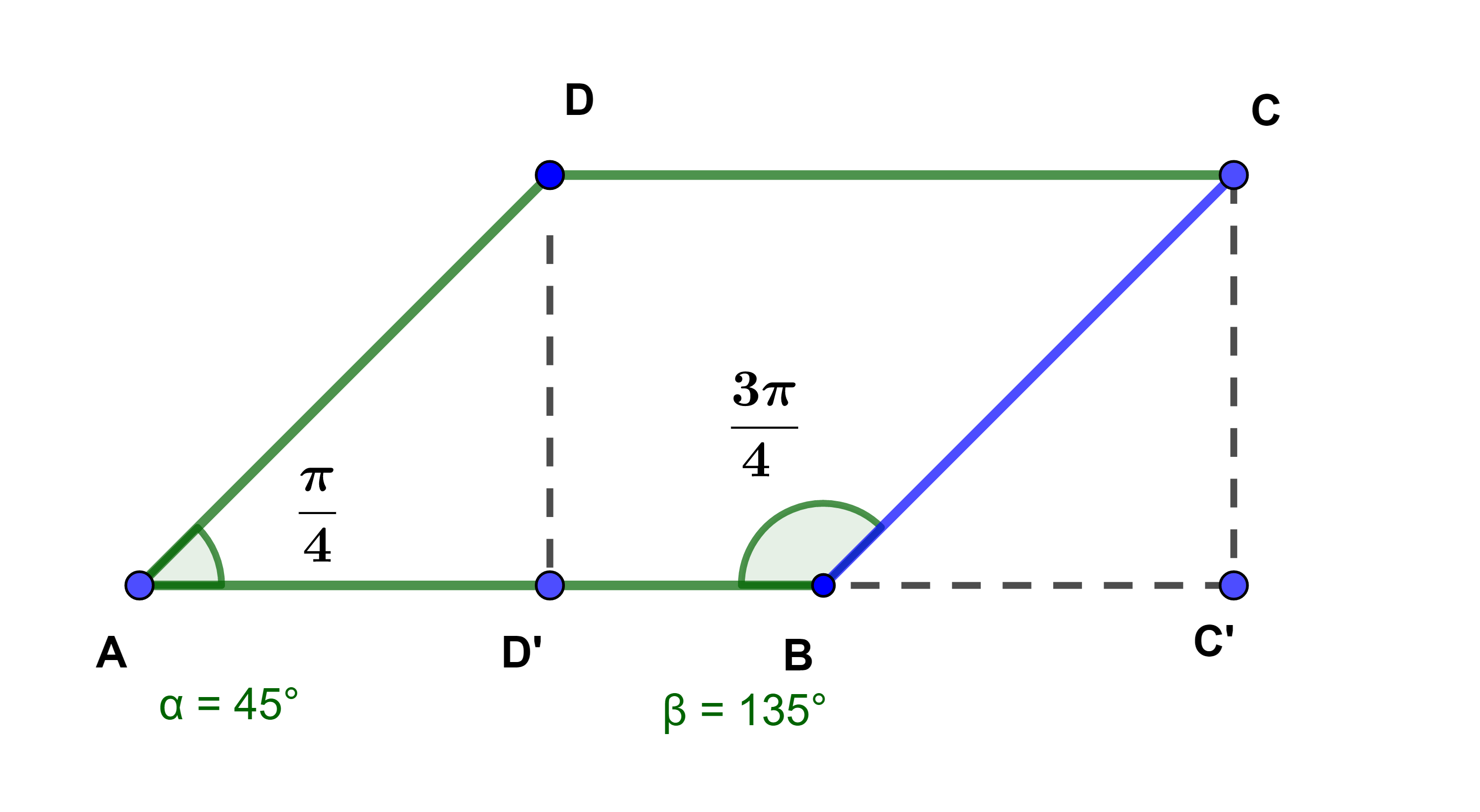
ليكن ABCD متوازي أضلاع بحيث AB= 5 و AD=3√2 و Â=45°.
نعتبر C' و D' المسقطين العموديين على التوالي للنقطتين C و D على (AB).
1) انشئ C' و D'.
2) احسب AD' و AB×AD'.
العدد الحقيقي AB×AD' يسمى الجذاء السلمي للمتجهتين AB→ و AD→ ونرمز له ب AB→.AD→.
3) احسب BC' و -BA×BC'.
العدد الحقيقي -BA×BC' يسمى الجذاء السلمي للمتجهتين BA→ و BC→ ونكتب BA→.BC→.
ملاحظة
لدينا AD'=ADcos(AB→;AD→)
اذن AB→.AD→=AB×ADcos(AB→;AD→).
1.1.2 تعريف
لتكن u→ و v→ متجهتين بحيث u→=AB→ و v→=AC→ و C' المسقط العمودي للنقطة C على (AB).
الجداء السلمي للمتجهتين u→ و v→
ونرمز له ب u→.v→ هو عدد حقيقي معرف كما يلي
1) الحالة الأولى u→ و v→ مستقيميتان.
(a) اذا كانت للمتجهتين u→ و v→ نفس المنحى
فان u→.v→=AB×AC.
(b) اذا كانت للمتجهتين u→ و v→ منحنين متقابلين
فان u→.v→=- AB×AC.
2) الحالة الثانية u→ و v→ غير مستقيميتان
u→.v→=AB→.AC'→.
ملاحظة
اذا كانت للمتجهتين AB→ و AC'→ منحيين متقابلين فان u→.v→=-AB×AC'.
اذا كانت للمتجهتين AB→ و AC'→ نفس المنحى فان u→.v→=AB×AC'.
مثال
ليكن ABCD مربعا مركزه O وطول ضلعه 3.
احسب
| AB→.AC→ | AB→.DC→ | |
| OC→.OA→ | AD→.CB→ |
تصحيح
1) AB→.AC→ = ?
B هي المسقط العمودي للنقطة C على (AB)
اذن AB→.AC→=AB×AB
=AB=9.
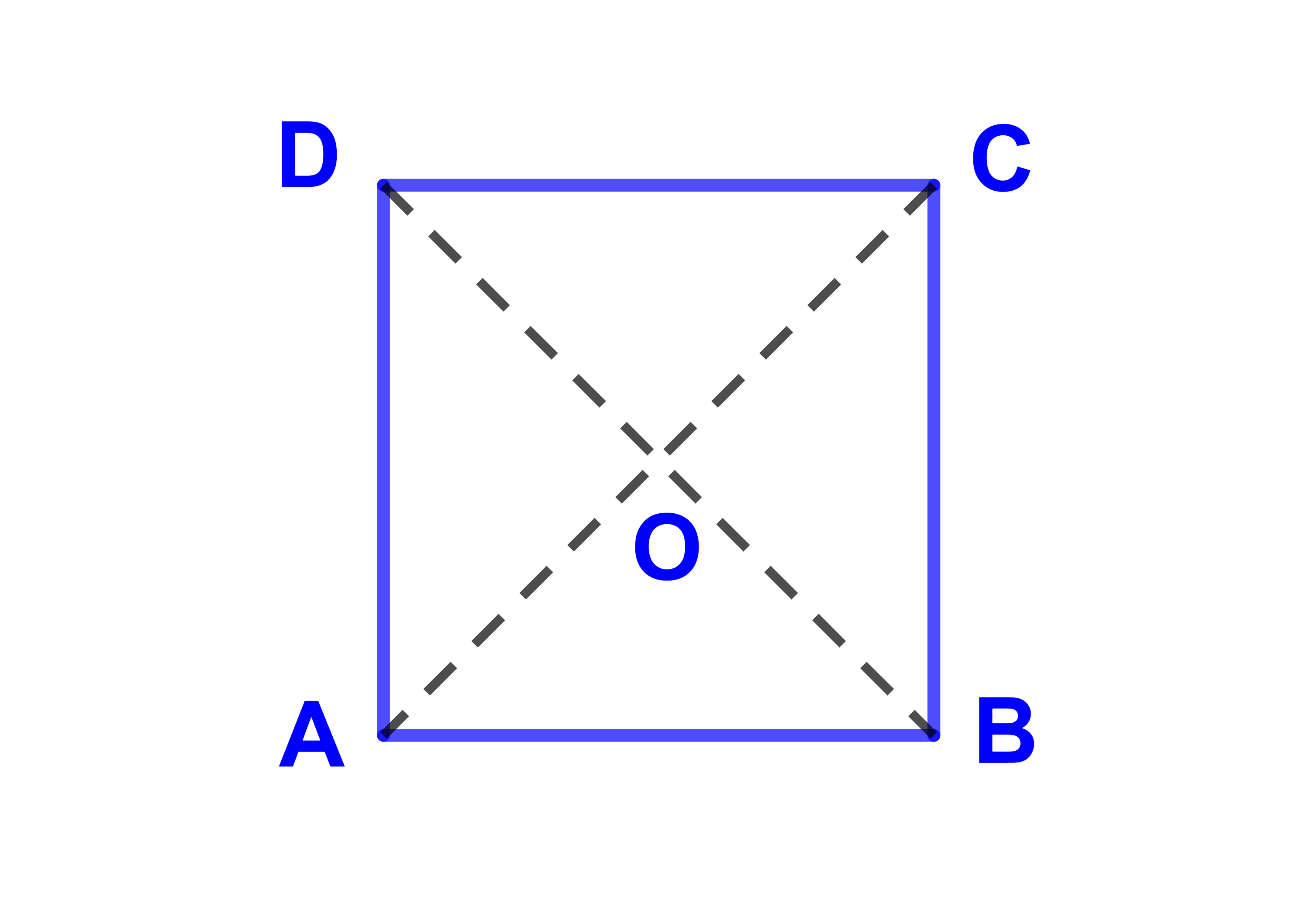
2) AB→ و DC→ متجهتان متساويتان
اذن مستقيميتان ولهما نفس المنحى
وبالتالي AB→.DC→=AB²=9.
3) OC→ و OA→ متجهتان متقابلتان اذن
| OC→.OA→ = - OA² = -( | 1 | AC)² |
| 2 |
AC²=AB²+BC²=9+9=18 وبالتالي
| OC→.OA→ = | -9 |
| 2 |
4) AD→ و CB→ متجهتان متقابلتان اذن مستقيميتان ولهما منحيان متقابلان
وبالتالي AD→.CB→=-AD×CB=-AD²=-9.