Le produit scalaire (1)
Produit scalaire de deux vecteurs
1.1 Définition et propriétés
1.1.1 Activité
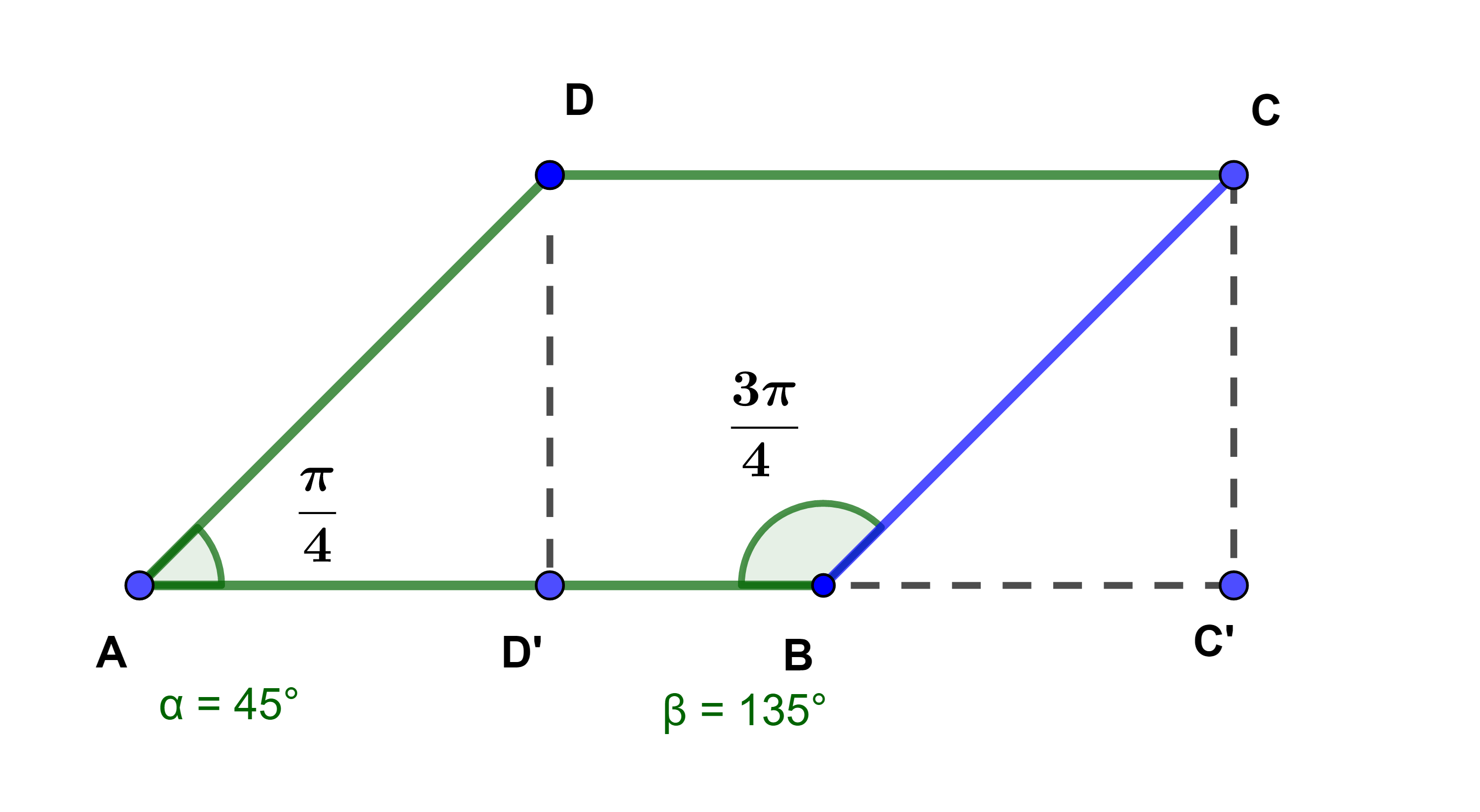
Soit ABCD un parallélogramme tels que AB= 5 ; AD=3√2 et Â=45°. On considère D' et C' les projetés orthogonaux respectifs de D et C sur (AB).
1) Tracer D' et C'.
2) Calculer AD' et AB×AD'.
Le nombre réel AB×AD' est appelé le Produit scalaire des vecteurs AB→ et AD→ et est noté AB→.AD→.
3) Calculer BC' et -BA×BC'.
le nombre réel -BA×BC' est appelé le Produit scalaire des vecteurs BA→ et BC→ et est noté BA→.BC→.
Remarque
On a AD'=ADcos(AB→;AD→)
donc AB→.AD→=AB×ADcos(AB→;AD→).
1.1.2 Définition
Soient u→ et v→ deux vecteurs tels que u→=AB→ et v→=AC→ et soit C' le projeté orthogonal de C sur (AB).
Le Produit scalaire de u→ et v→, noté u→.v→ est un nombre réel défini par
1) Premier cas u→ et v→ sont colinéaires alors
(a) Si u→ et v→ sont de même sens alors
u→.v→=AB×AC.
(b) Si u→ et v→ sont de sens opposé alors
u→.v→=- AB×AC.
2) Deuxième cas u→ et v→ ne sont pas colinéaires
alors u→.v→=AB→.AC'→.
Remarque
Si AB→ et AC'→ sont de sens contraire alors u→.v→=-AB×AC'.
Si AB→ et AC'→ sont de même sens alors u→.v→=AB×AC'.
Exemple
Soit ABCD un carré de centre O et de coté 3.
Calculer
| AB→.AC→ | AB→.DC→ | |
| OC→.OA→ | AD→.CB→ |
Correction
1) AB→.AC→ = ?
B est le projeté orthogonal de C sur (AB)
donc AB→.AC→=AB×AB
=AB=9.
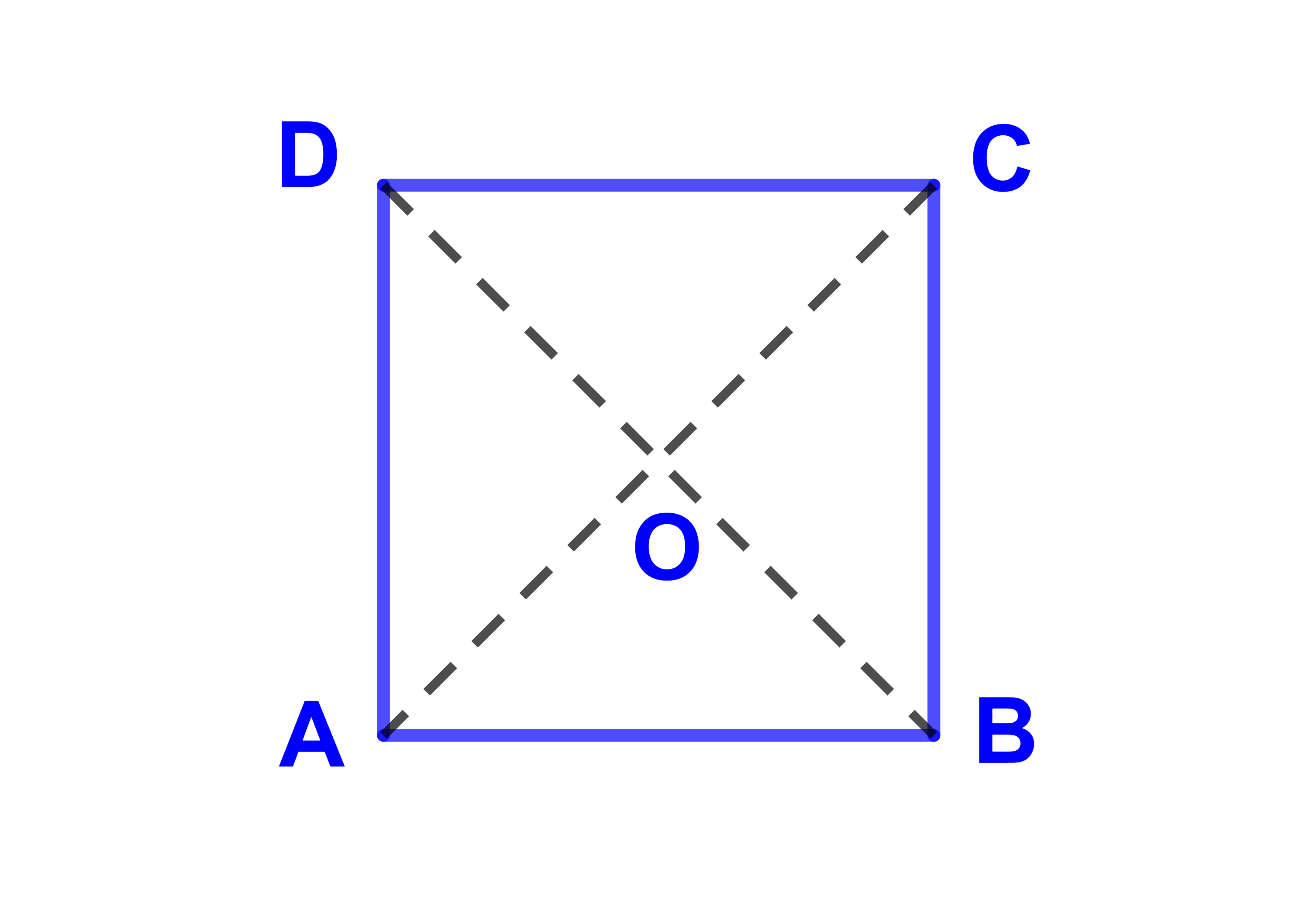
2) AB→ et DC→ sont égaux
donc sont colinéaires et de même sens
alors AB→.DC→=AB²=9.
3) OC→.OA→ = ?
Puisque OC→ et OA→ sont opposés alors
| OC→.OA→ = - OA² = -( | 1 | AC)² |
| 2 |
AC²=AB²+BC²=9+9=18 alors
| OC→.OA→ = | -9 |
| 2 |
4) AD→ et CB→ sont opposés donc sont colinéaires et de sens contraires
alors AD→.CB→=-AD×CB=-AD²=-9.