1- المعلم واحداثيتا نقطة ومتجهة

1.1 المعلم في المستوى

1.1.1 تعريف

ليكن (OI) و (OJ) محورين متدرجين ومتقاطعين في نقطة في نقطة O.
المثلوث (O;OI^→;OJ^→) يسمى معلما في المستوى.

1.1.2 المعلم المتعامد الممنظم

المعلم المتعامد
اذا كان (O;OI^→;OJ^→) معلما في المستوى بحيث (OI)⊥(OJ) فانه يسمى معلما متعامدا.

المعلم المتعامد الممنظم
اذا كان المعلم (O;OI^→;OJ^→) معلما متعامدا بحيث OI=OJ فانه يسمى معلما متعامدا ممنظما.

ملاحظة
في هذا الدرس نعتبر المستوى منسوبا الى معلم متعامد ممنظم
(O;i^→;j^→).

1.2 احداثيتا نقطة ومتجهة

1.2.1 تقديم

ليكن (OI) و (OJ) محورين متدرجين ومتقاطعين في نقطة في نقطة O.
لتكن M نقطة من المستوى
المستقيم الموازي للمحور (OJ) والمار من النقطة M يقطع المحور (OI) في نقطة H.
والمستقيم الموازي للمحور (OI) والمار من النقطة M يقطع المحور (OJ) في نقطة K.

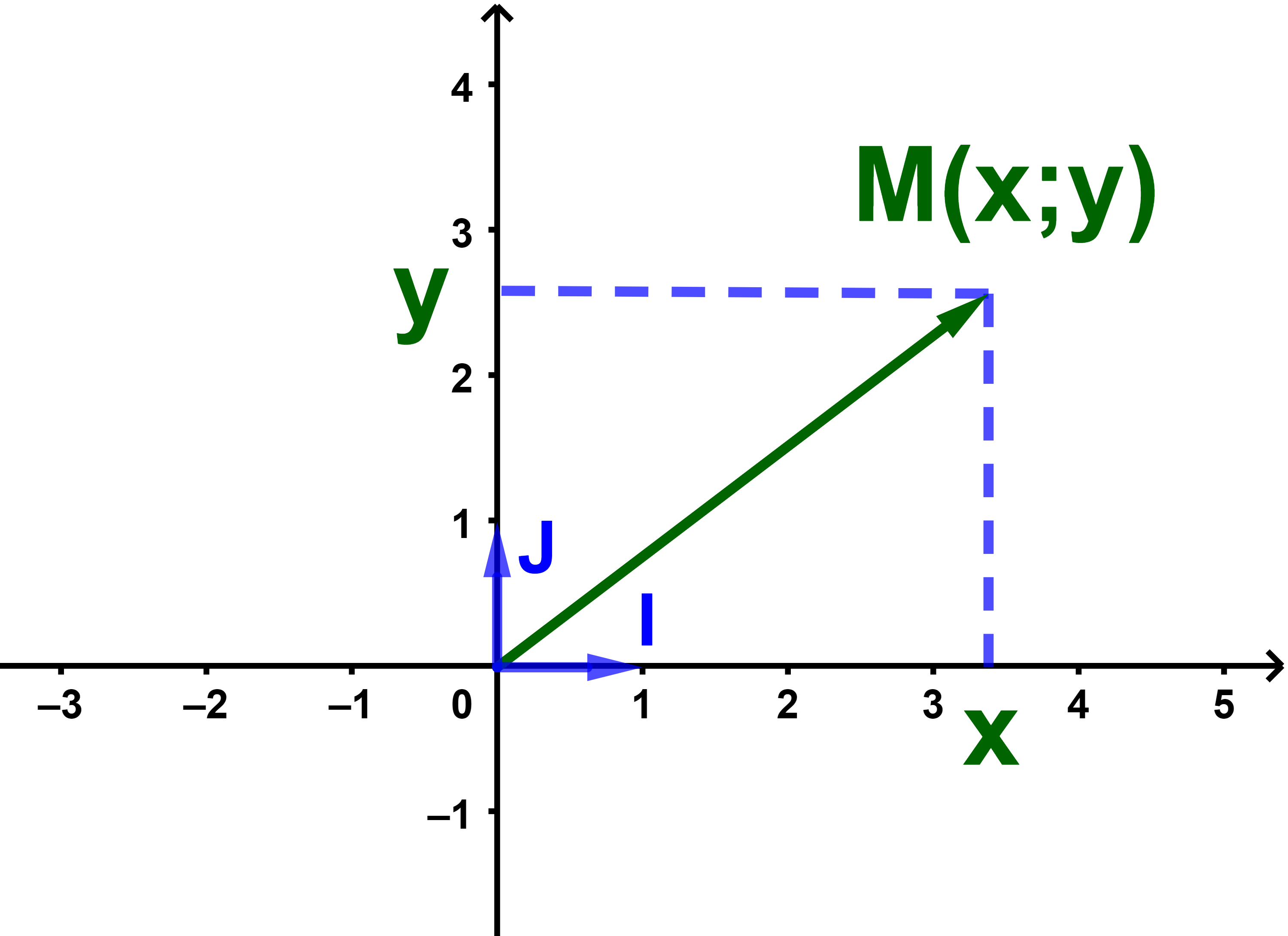
اذا كان x أفصولا للنقطة H في المحور (OI)
و y أفصولا للنقطة K في المحور (OJ)
فان x و y احداثيتا النقطة M ونكتب M(x;y).
العدد x يسمى أفصولا للنقطة M و y أرتوبا للنقطة M
x و y هما أيضا احداثيتا المتجهة OM^→
ونكتب OM^→(x;y).

1.2.2 خاصيات

المستوى ℙ منسوب الى معلم متعامد ممنظم
(O;i^→;j^→).
1) لكل نقطة M من المستوى يوجد زوج وحيد
(x;y) بحيث OM^→=xi^→+yj^→
ونكتب M(x;y).
2) لكل متجهة u^→ يوجد زوج وحيد (x;y) بحيث u^→=xi^→+yj^→ ونكتب u^→(x;y).

تمرين 1 tp

انطلاقا من المعلم التالي حدد احداثيتات النقط A و B و C و D و E.

تمرين 2 tp

المستوى ℙ منسوب الى معلم متعامد ممنظم (O;i^→;j^→).
انشئ النقط A(-2;0) و B(1;3) و C(0;4) و E(-3;-2).

ملاحظات
لتكن F(a;b) نقطة من المستوى
1) F تنتمي الى محور الافاصيل (Ox) يعني b=0
2) F تنتمي الى محور الاراتيب (Oy) يعني a=0
3) a = b = 0 يعني F = O اصل المعلم

مثال O(0;0) اصل المعلم.