الاحصاء (2)
2- التمثيلات المبيانية
2.1 التمثيلات بالعصا
مثال
نعتبر متساسلة احصائية معرفة بالجدول التالي
| xi | 1 | 2 | 3 | 4 | 5 | |
| ni | 4 | 3 | 5 | 3 | 5 | |
| Ni | 4 | 7 | 12 | 15 | 20 | |
| fi | 0,2 | 0,15 | 0,25 | 0,15 | 0,25 |
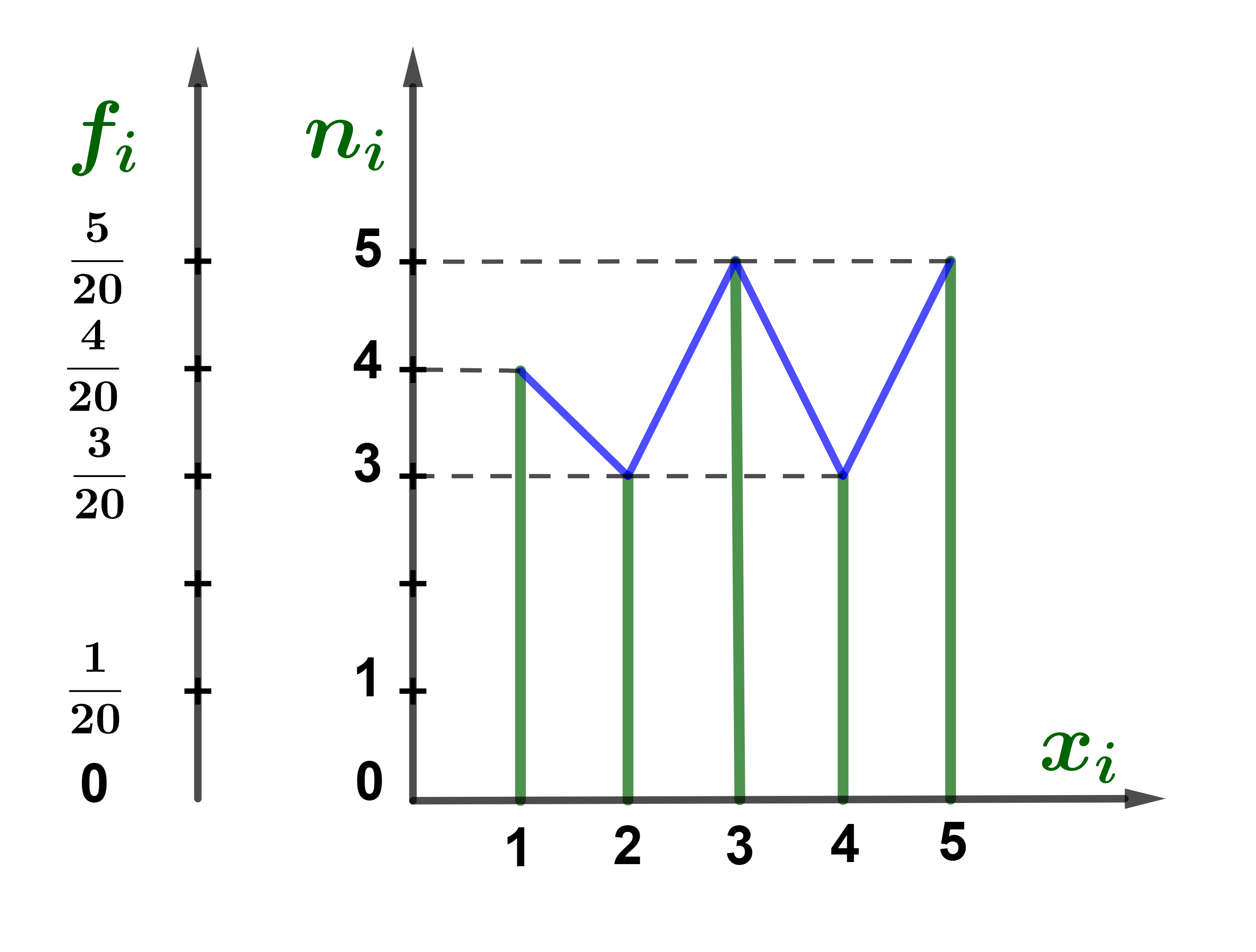
هذا المبيان يسمى تمثيلا مبيانيا بالعصا للحصيصات ويمكن اعتباره تمثيلا مبيانيا للترددات وذلك بتغيير وحدات المعلم
2.2 القطاع الدائري
مثال
نعتبر متساسلة احصائية معرفة بالجدول التالي
| xi | 1 | 2 | 3 | 4 | 5 | |
| ni | 3 | 5 | 2 | 8 | 7 | |
| fi | 0,12 | 0,2 | 0,08 | 0,32 | 0,28 | |
| pi | 12% | 20% | 8% | 32% | 28% | |
| الزاوية | 43,2° | 72° | 28;8° | 115,2° | 100,8° |
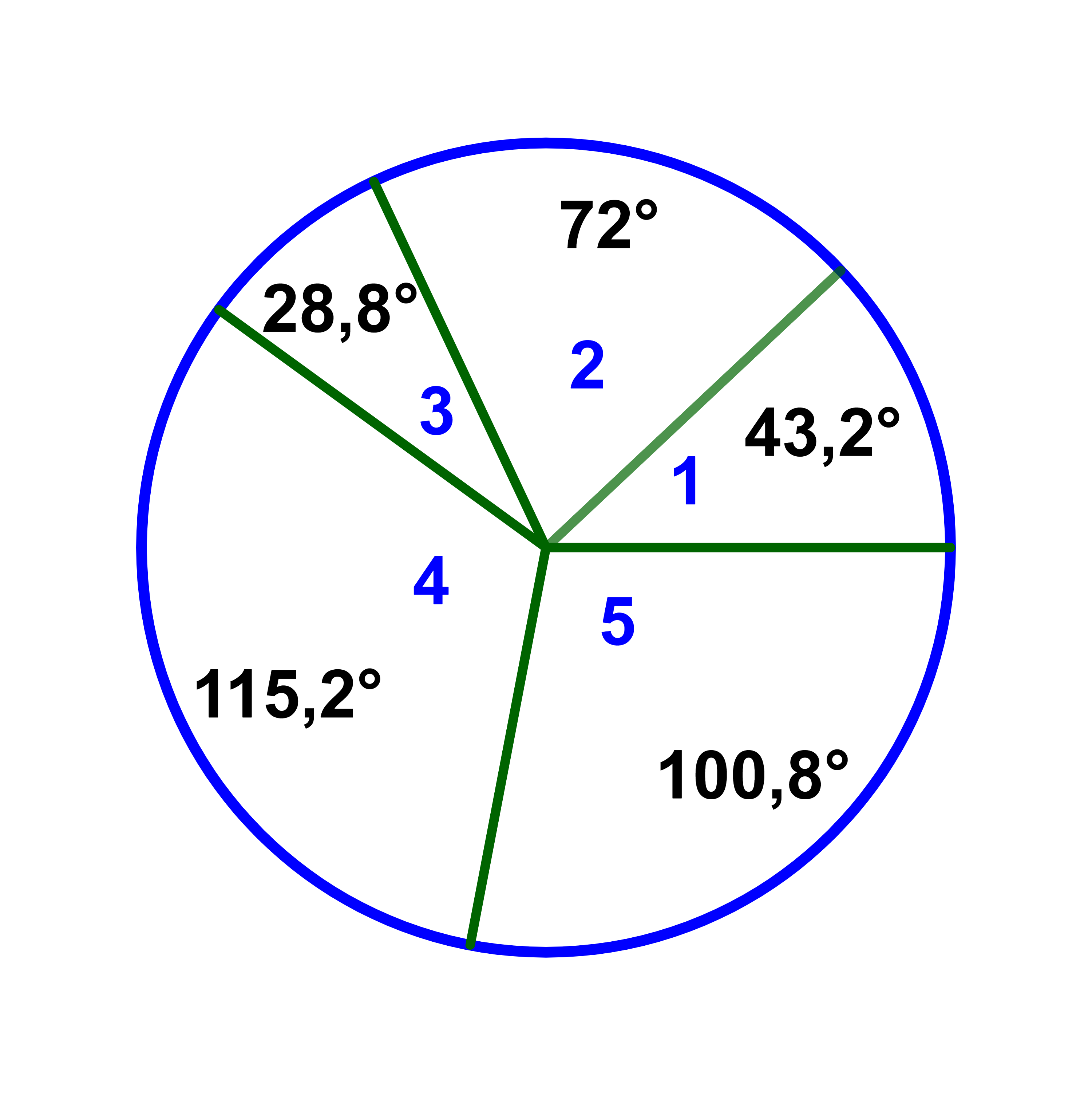
2.3 المدراج
مثال لميزة متصلة
يحدد الجدول التالي عدد مشاهدات منشور على شبكة التواصل الاجتماعي كل 35 دقيقة.
| Ci | [0;35[ | [35;70[ | [70;105[ | [105;140[ | [140;175[ | |
| ni | 1000 | 750 | 2000 | 750 | 500 | |
| Ni | 1000 | 1750 | 3750 | 4500 | 5000 | |
| fi | 0,2 | 0,15 | 0,4 | 0,15 | 0,1 | |
| Fi | 0,2 | 0,35 | 0,75 | 0,9 | 1 | |
| pi | 20% | 15% | 40% | 15% | 10% |
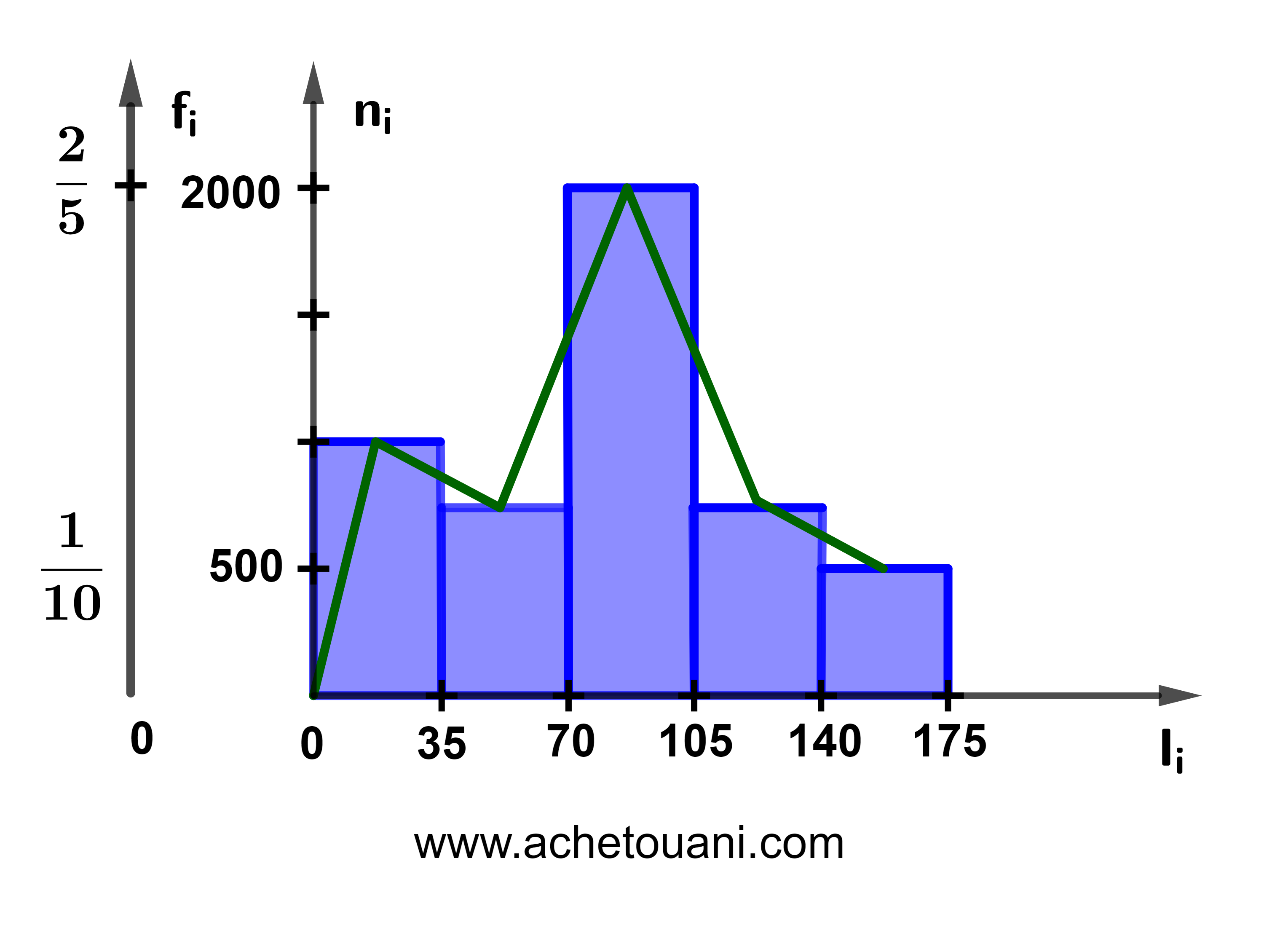
هذا المبيان يسمى تمثيلا مبيانيا بالمدراج للحصيصات ويمكن اعتباره مدراجا للترددات وذلك بتغيير وحدات المعلم.
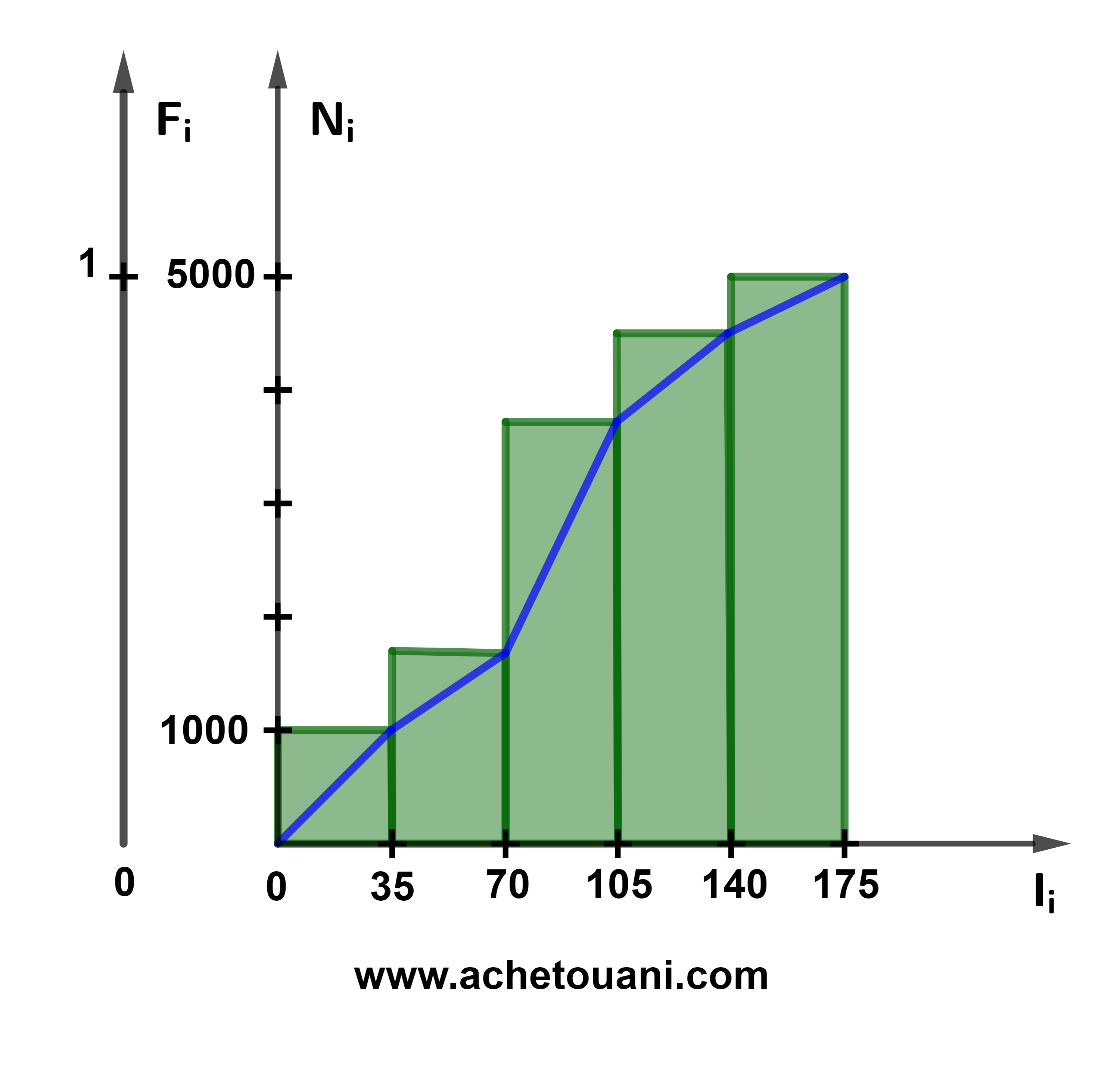
هذا المبيان يسمى تمثيلا مبيانيا بالمدراج للحصيصات المتراكمة ويمكن اعتباره مدراجا للترددات المتراكمة وذلك بتغيير وحدات المعلم.