Statistique (7)
Exercice 1 tp
On considère une série statistique définie par le tableau suivant.
1) Construire l'histogramme des effectifs cumulés et le point H d'ordonnée est égale à la moitie d'effectif total sur le polygône des effectifs cumulés.
2) Déterminer un encadrement de l'abscisse de H.
3) Calculer la médiane.
| Ci | [1 ; 5[ | [5 ; 9[ | [9 ; 13[ | [13 ; 17[ | [17 ; 21[ | |
| ni | 50 | 70 | 50 | 120 | 110 |
Correction
1) On trace d'abord le tableau des effectifs cumulés.
| Ci | [1 ; 5[ | [5 ; 9[ | [9 ; 13[ | [13 ; 17[ | [17 ; 21[ | |
| ni | 50 | 70 | 50 | 120 | 110 | |
| Ni | 50 | 120 | 170 | 290 | 400 |
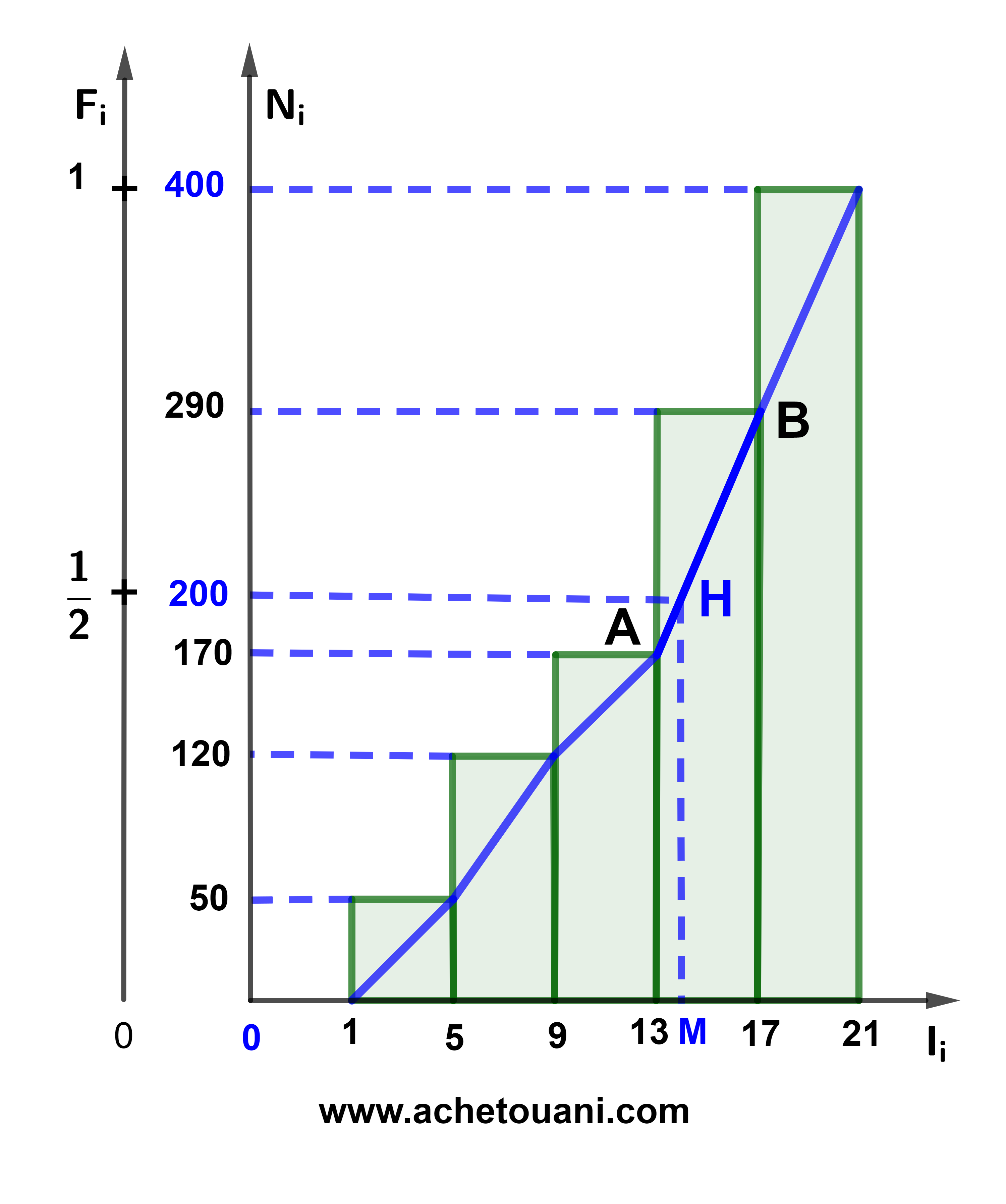
2) On a N=400 donc N÷2=200 on désigne par M à l'abscisse de H d'ordonnée 200.
Graphiquement on déduit un encadrement de la médiane M.
13<M<17.
3) On détermine M
Rapel
Equation de la droite (AB) tels que
A(xA;yA) ; B(xB;yB) ;
xA ≠ xB et yA ≠ yB.
M(x;y)∈(AB) signifie
| x - xA | = | y - yA |
| xB - xA | yB - yA |
H(M;200)∈(AB) tels que A(13;170) et B(17;290) signifie
| M - 13 | = | 200-170 |
| 17-13 | 290-170 | |
| M - 13 | = | 30 |
| 4 | 120 | |
| M=13 + | 120 | |
| 120 |
donc M=14.