2- التماثل المحوري

2.1 تعريف وتمثيل مبياني

2.1.1 تعريف

ليكن D مستقيما في المستوى.
التحويل الهندسي الذي يربط كل نقطة M من المستوى بنقطة M' بحيث (D) واسط القطعة [MM'] يسمى التماثل المحوري (D) ونرمز له ب S_D.

بتعبير آخر S_D(M)=M' يعني (D) واسط القطعة [MM'].

2.1.2 التمثيل المبياني

لتكن M نقطة و M' صورتها بتماثل المحوري S_D.

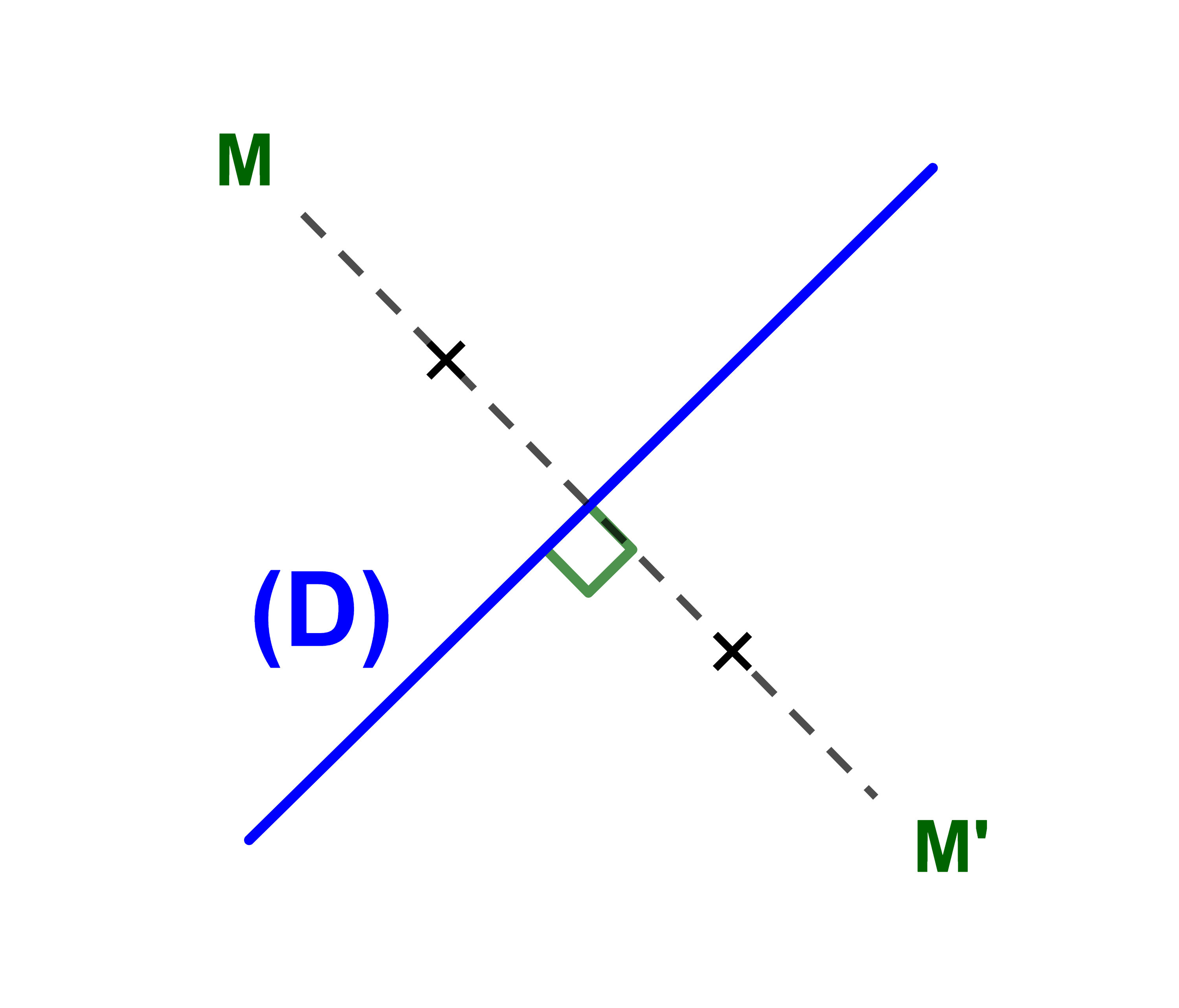
ملاحظات
1) صورة نقطة من (D) هي نفسها
نقول ان المحور (D) صامد بالتماثل المحوري S_(D).
2) اذا كان (D')⊥(D) فان (D') صامد اجمالي ب S_(D)
لكن النقطة الوحيدة من (D') الصامدة بالتماثل المحوري S_(D) هي نقطة تقاطع (D) و (D').

2.2 الحفاظ على معامل استقامية متجهتين بتماثل محوري

2.2.1 خاصية

التماثل المحوري يحافظ على معامل استقامية متجهتين.

2.2.2 نتيجة

التماثل المحوري يحافظ على استقامية النقط وعلى منتصف قطعة.

2.2.3 المسافة والتماثل المحوري

خاصية
ليكن S تماثلا محوريا.
مسافة نقطتين هي نفس مسافة صورتيهما بالتماثل المحوري S.
بتعبير آخر اذا كان S(A)=A' و S(B)=B' فان A'B'=AB.

نتيجة
التماثل المحوري يحافظ على المسافة.