الحساب المثلثي (1_1)
1- العلاقة بين الدرجة والراديان والغراد
1.1 صيغ التحويل
1.1.1 تقديم
1) الدرجة 90° ; زاوية مستقيمية قياسها 180°; دائرة تمثل زاوية قياسها 360° تسمى كذلك بزاوية ممتلئة.
2) الغراد 180° توافق
200 غراد.
3) الراديان: 1 راديان هو وحدة قياس زاوية تحصر قوس دائري طوله يساوي طول شعاع الدائرة
بالتقريب
1 rad≅57,3°
محيط نصف دائرة شعاعها R يساوي πR,
لدينا اذن
180°=πrad
ودائرة تمثل زاوية قياسها
2πrad.
1.1.2 صيغ التحويل
| x° | = | y rad | = | z grad |
| 180 | π | 200 |
تحويل 1 tp
حول الى الراديان
| 20° | 50° | 150° | 275° |
تصحيح
ليكن x و y و z على التوالي قياسات بالدرجة والراديان والغراد.
| x | = | y | = | z |
| 180 | π | 200 |
ومنه فان
| الدرجة | 20° | 50° | 270° | 400° | ||||
| الراديان | π | 5π | 3π | 20π | ||||
| 9 | 18 | 2 | 9 |
2- الدائرة المثلثية والافاصيل المنحنية لنقطة
2.1 الدائرة المثلثية
2.1.1 تقديم
لتكن (C) دائرة مركزها O وشعاعها R ونعتبر نقطة A من الدائرة (C) كأصل لها.
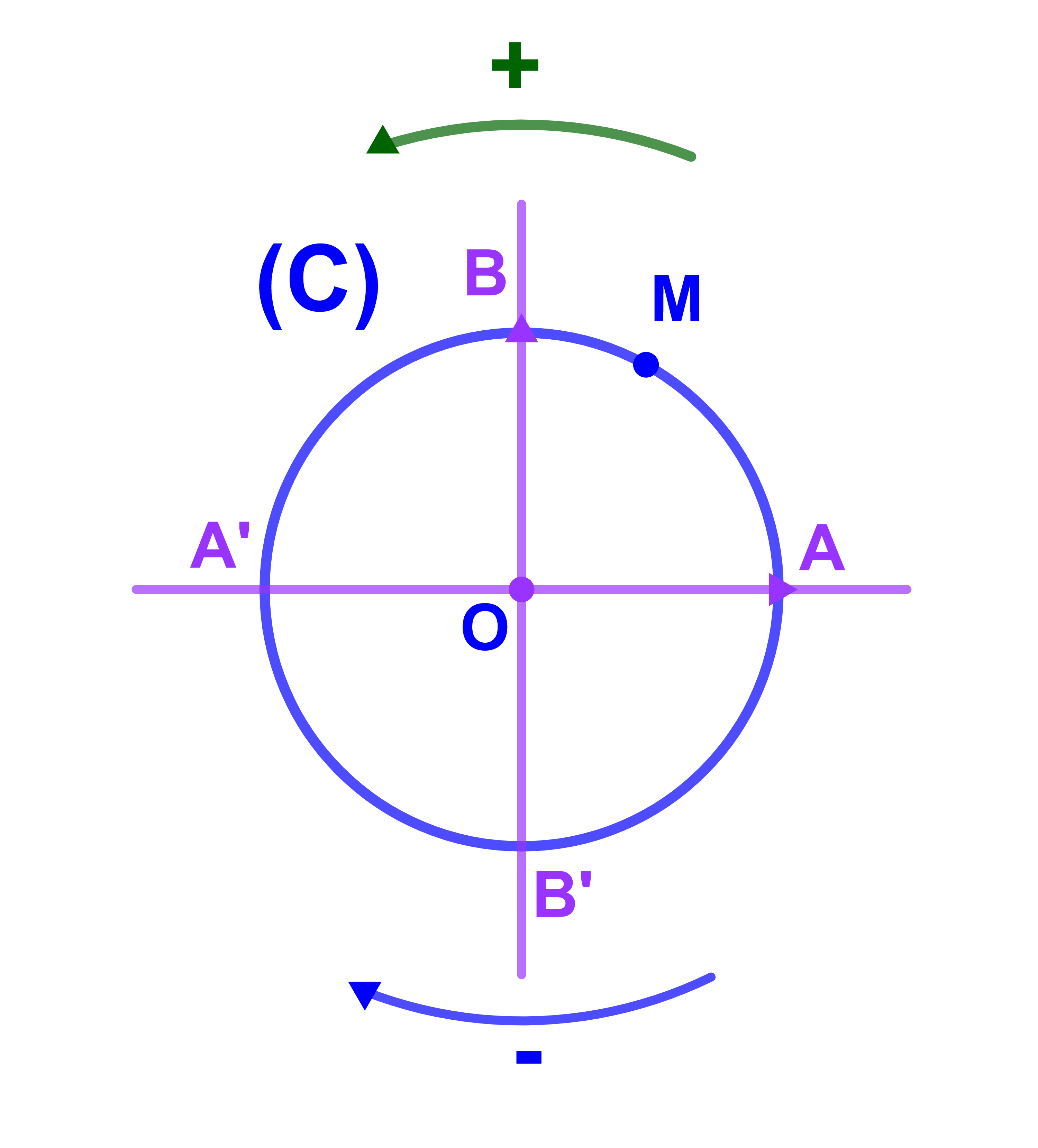
لتكن M نقطة من (C). توجد امكانيتان للانتقال على الدائرة من A الى M
1) اما الاتجاه عكس عقارب الساعة ويسمى
الاتجاه المباشر أو الاتجاه الموجب .
2) واما الانتقال في الاتجاه العكسي ويسمى
الاتجاه غير المياشر او الاتجاه السالب
وعندما نعين اتجاها على الدائرة نقول ان الدائرة موجهة.
اذا كانت جميع دوائر المستوى موجهة في اتجاه واحد فاننا نقول ان المستوى موجها.
2.1.2 تعريف
الدائرة المثلثية ونرمز لها ب (C),
هي دائرة موجهة مركزها O وشعاعها 1 وأصلها A نقطة.
المعلم المتعامد الممنظم (O;OA→;OB→) يسمى معلما متعامدا ممنظما مباشرا مرتبطا بالدائرة الثلثية (C).