الحساب المثلثي (1_2)
2.2 الافاصيل المنحنية لنقطة
2.2.1 تقديم
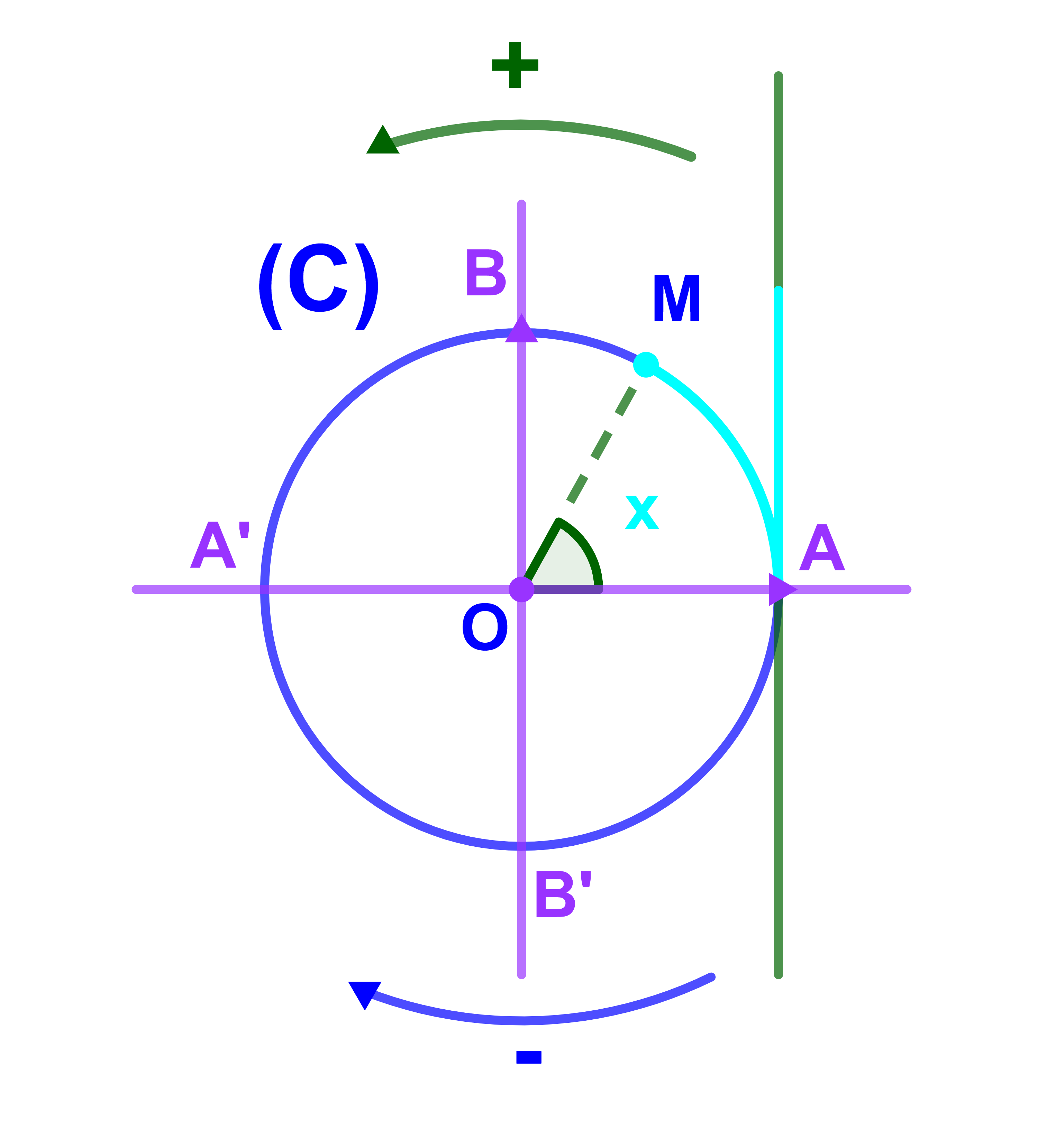
لتكن M نقطة من الدائرة المثلثية التي أصلها النقطة A و x قياس القوس AM.
1) الانتقال على الدائرة (C) انطلاقا من أصلها A في الاتجاه الموجب الى M.
| عدد الدوران | 1 | 2 | .. | n |
| المسافة المقطوعة | x+2π | x+4π | .. | x+2nπ |
2) الانتقال على الدائرة (C) انطلاقا من أصلها A في الاتجاه السالب الى M.
| عدد الدوران | 1er | 2 | .. | n |
| المسافة المقطوعة | x-2π | x-4π | .. | x-2nπ |
ملاحظة
الاشارة (-) أمام
2π ترجع الى الاتجاه السالب.
في الحالتين هذه القياسات تكتب على الشكل
x+2kπ حيث k∈ℤ.
2.2.2 تعريف
لتكن M نقطة من الدائرة المثلثية (C) التي أصلها النقطة A و x∈IR بحيث |x| قياس القوس المحدد بالنقطتين A و M.
الأعداد x+2kπ حيث k∈ℤ تسمى
الأفاصيل المنحنية للنقطة M
ونكتب M(x+2kπ).
العدد الطبيعي |k| هو عدد الدوران.
النقطة M تسمى صورة الأعداد الحقيقية x+2kπ.
2.2.3 امثلة
A(2kπ) أصل الدائرة المثلثية.
A'(-π+2kπ) او A'(π+2kπ)
حيث k∈ℤ.
| B( | π | +2kπ) = B( | - 3π | +2kπ) |
| 2 | 2 | |||
| B'( | - π | +2kπ) = B'( | 3π | +2kπ) |
| 2 | 2 |
2.3 الأفصول الرئيسي لنقطة
2.3.1 تعريف
الأفصول الرئيسي لنقطة M من الدائر المثلثية (C) هو الأفصول المنحني للنقطة
M
والذي ينتمي الى المجال ]-π;π] وهو وحيد.
نتيجة
اذا كان x=y+2kπ بحيث k∈ℤ فان x و y يمثلان نفس النقطة على الدائرة المثلثية (C).
ونكتب x≡y[2π] ونقرأ x يوافق y بترديد
2π.
x≡y[2π] يعني x=y+2kπ بحيث k∈ℤ.
2.3.2 مثال
لتكن A(x) و B(y) نقطتين من الدائرة المثلثية (C) بحيث
| y = | -3π | و | x = | 10π |
| 5 | 7 |
للتذكير الأقصول الرئيسي لنقطة من الدائرة المثلثية (C) هو أفصول منحني وينتمي الى المجال I=]-π;π].
| x = | 10π | ∉ I=]- π ;π] |
| 7 |
اذن x ليس أفصولا رئيسيا للنقطة A(x).
| y = | - 3π | ∈ I=]- π ;π] |
| 5 |
اذن y أفصولا رئيسيا للنقطة B(y).