Trigonométrie (1_1)
1- Relation entre degré, radian et grade
1.1 Formules de conversion
1.1.1 Introduction
1) Degré: un angle droit mesure 90° ; un angle plat mesure 180°; un cercle représente un angle de 360° appelé angle plein.
2) Grade: 180° vaut 200 grades.
3) Radian: 1 radian est l'unité de mesure d'angle interceptant sur la circonférence d'un cercle, un arc de longueur égale au rayon.
1 radian≅57,3°
Le périmètre d'un demi cercle de rayon R est πR.
On a donc 180°=π radians
Un cercle représente un angle de 2π radians.
1.1.2 Les formules de conversion
| x° | = | y rad | = | z grad |
| 180 | π | 200 |
Exercice 1 tp
Convertir en radians
| 20° | 50° | 150° | 275° |
Correction
x ; y et z sont respectivement en dégré ; radians et grade.
| x | = | y | = | z |
| 180 | π | 200 |
ainsi
| Degré | 20° | 50° | 270° | 400° | ||||
| Radians | π | 5π | 3π | 20π | ||||
| 9 | 18 | 2 | 9 |
2- Cercle trigonométrique Les abscisses curvilignes
2.1 Cercle trigonométrique
2.1.1 Introduction
Soit (C) un cercle de centre O et de rayon R. On fixe un point A sur (C) et on le considère comme origine du cercle (C).
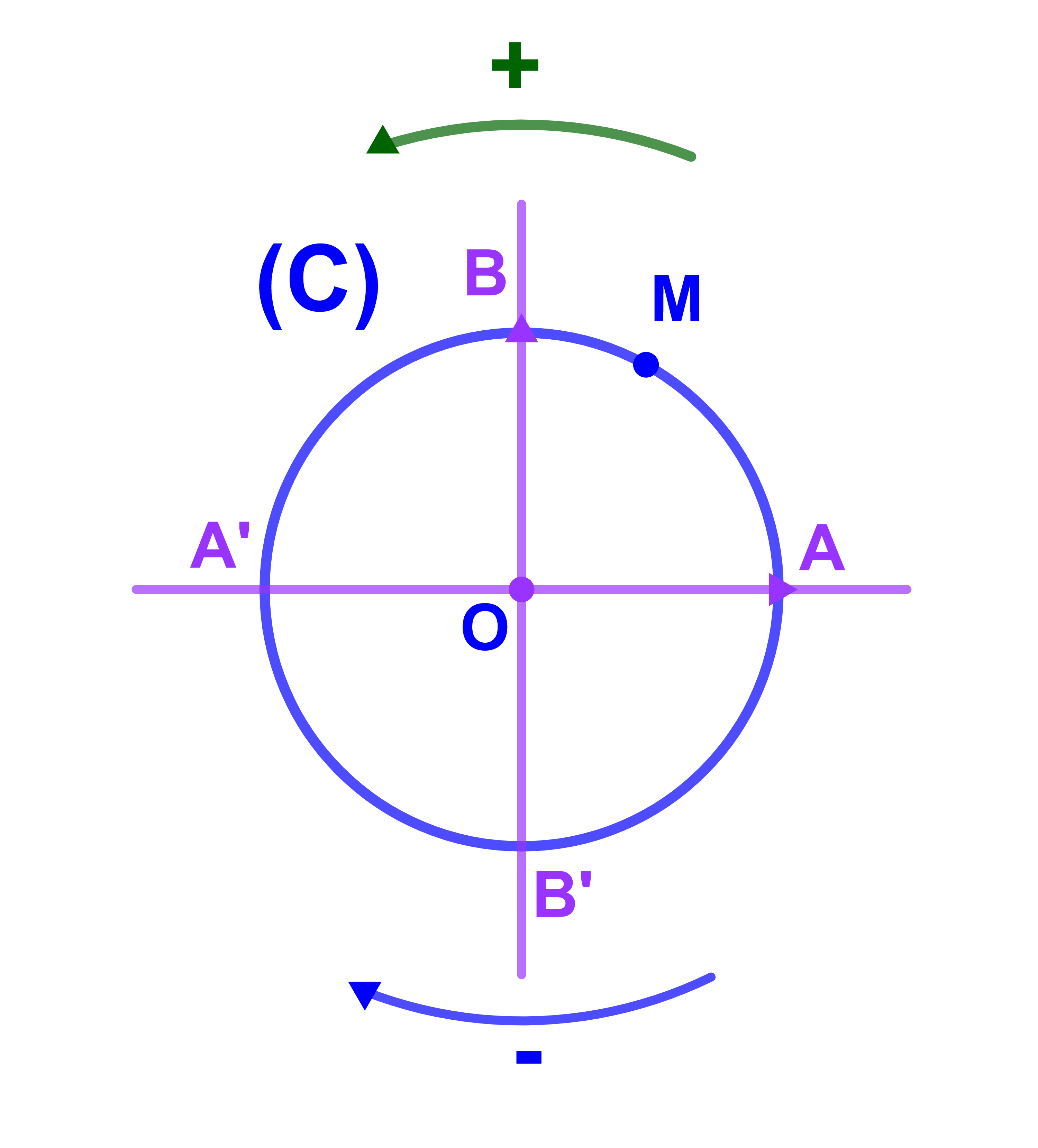
On considère un point M de (C). Pour se déplacer sur le cercle de A à M,
il y'a deux possibilités: soit on prend le sens antihoraire
(qui contrairiait le sens des aiguilles du montre) et serait nommé
sens direct ou sens positif
soit l'autre sens et serait nommé sens indirect ou sens négatif.
Si on désigne un sens pour un cercle, on dit que ce cercle est orienté.
Si tous les cercles du plan sont orientés de même sens alors on dit que le plan est orienté.
2.1.2 Définition
Un cercle orienté de centre O et de rayon 1 et d'origine un point A est appelé cercle trignmétrique et est noté (C).
Le repère orthonormé (O;OA→;OB→) est
un repère orthonormé direct lié au cercle trigonométrique (C).