Trigonométrie (1_2)
2.2 Les abscisses curvilignes d’un point
2.2.1 Introduction
Soit M un point du cercle trigonométrique d'origine A et x la mesure de l'arc AM.
1) Le point M se deplace sur (C) de l'origine A dans le sens positif.
| Nombre de tour |
1 | 2 | .. | n |
| Distance parcourait |
x+2π | x+4π | .. | x+2nπ |
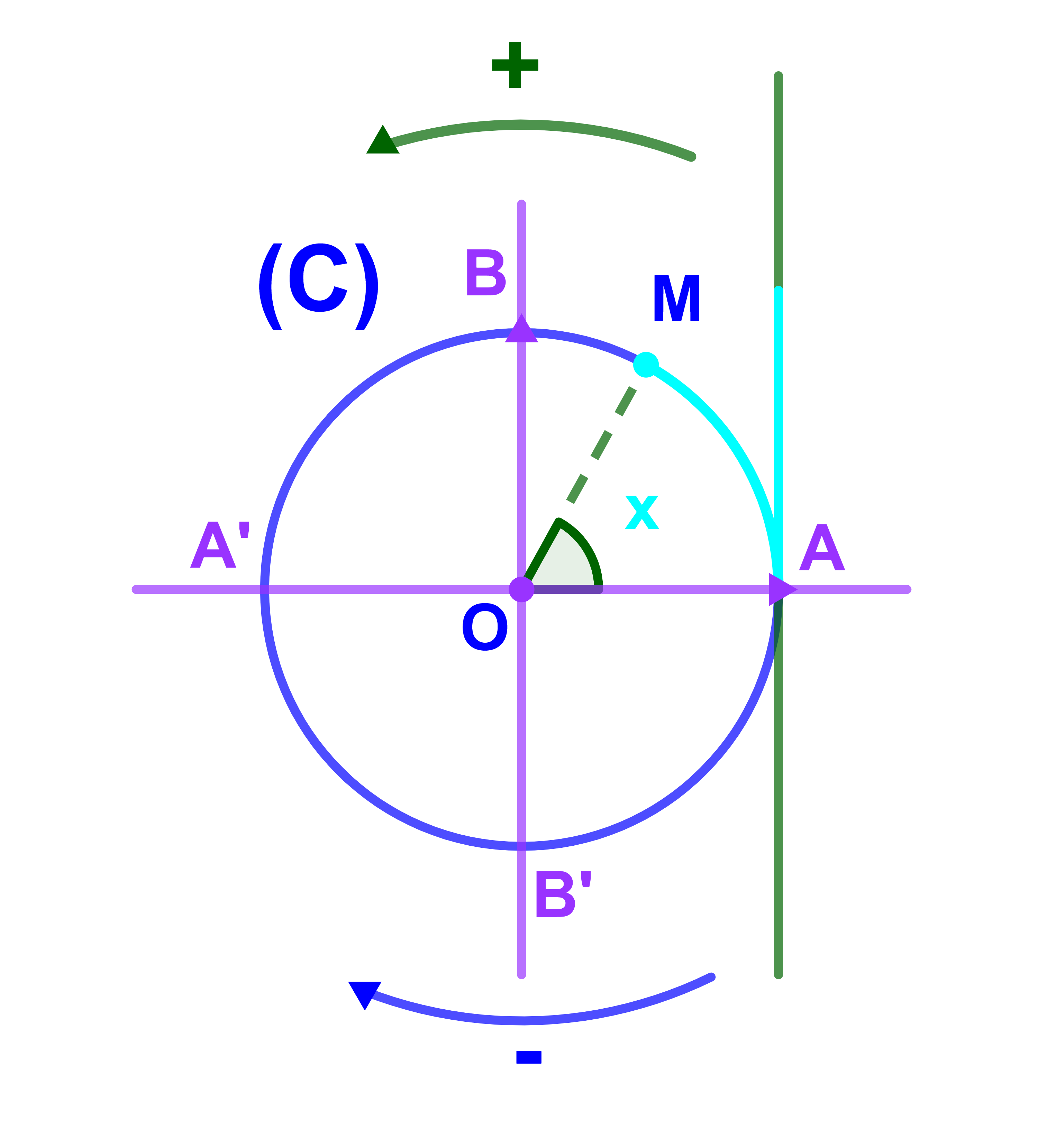
2) Le point M se déplace sur (C) de l'origine A dans le sens négatif.
| Nombre de tour |
1er | 2 | .. | n |
| Distance parcourait |
x-2π | x-4π | .. | x-2nπ |
Remarques
Le signe (-) devant 2π est dû à la direction négative.
Dans les deux cas, ces mesures s'écrivent sous la forme x+2kπ tel que k∈ℤ.
2.2.2 Définition
Soient M un point du cercle trigonométrique (C) d'origine A et x∈IR telle que |x| la mesure de l'arc déterminé par A et M.
Les nombres x+2kπ tel que k∈ℤ sont appelés des abscisses curvilignes du point M et
on écrit M(x+2kπ).
L'entier naturel |k| est le nombre de tours.
Le point M est appelé image des nombres réels x+2kπ.
2.2.3 Exemples
A(2kπ) origine du cercle trigonométrique.
A'(-π+2kπ)= A'(π+2kπ)
k∈ℤ
| B( | π | +2kπ) = B( | - 3π | +2kπ) |
| 2 | 2 | |||
| B'( | - π | +2kπ) = B'( | 3π | +2kπ) |
| 2 | 2 |
2.3 Abscisse curviligne principale
2.3.1 Définition
L’abscisse curviligne principale d'un point M du cercle trigonométrique (C) est l’abscisse curviligne du point M qui se trouve dans l'intervalle ]-π;π] et il est unique.
Résultat
Si x=y+2kπ tel que k∈ℤ alors x et y représentent le même point dans (C)
et on écrit x≡y[2π] et on lit x est congru à y modulo 2π.
x≡y[2π] signifie x=y+2kπ tel que k∈ℤ.
2.3.2 Exemple
Soient A(x) et B(y) deux points du cercle trigonométrique tels que
| x = | 10π | et | y = | -3π |
| 7 | 5 |
Notons que l'abscisse principale d'un point est une abscisse curviline qui appartient à l'intervalle I=]-π;π].
| x = | 10π | ∉ I=]- π ;π] |
| 7 |
donc x n'est pas l'abscisse principale du point A(x).
| y = | - 3π | ∈ I=]- π ;π] |
| 5 |
donc y est l'abscisse principale du point B(y).