تمرين 1 tp

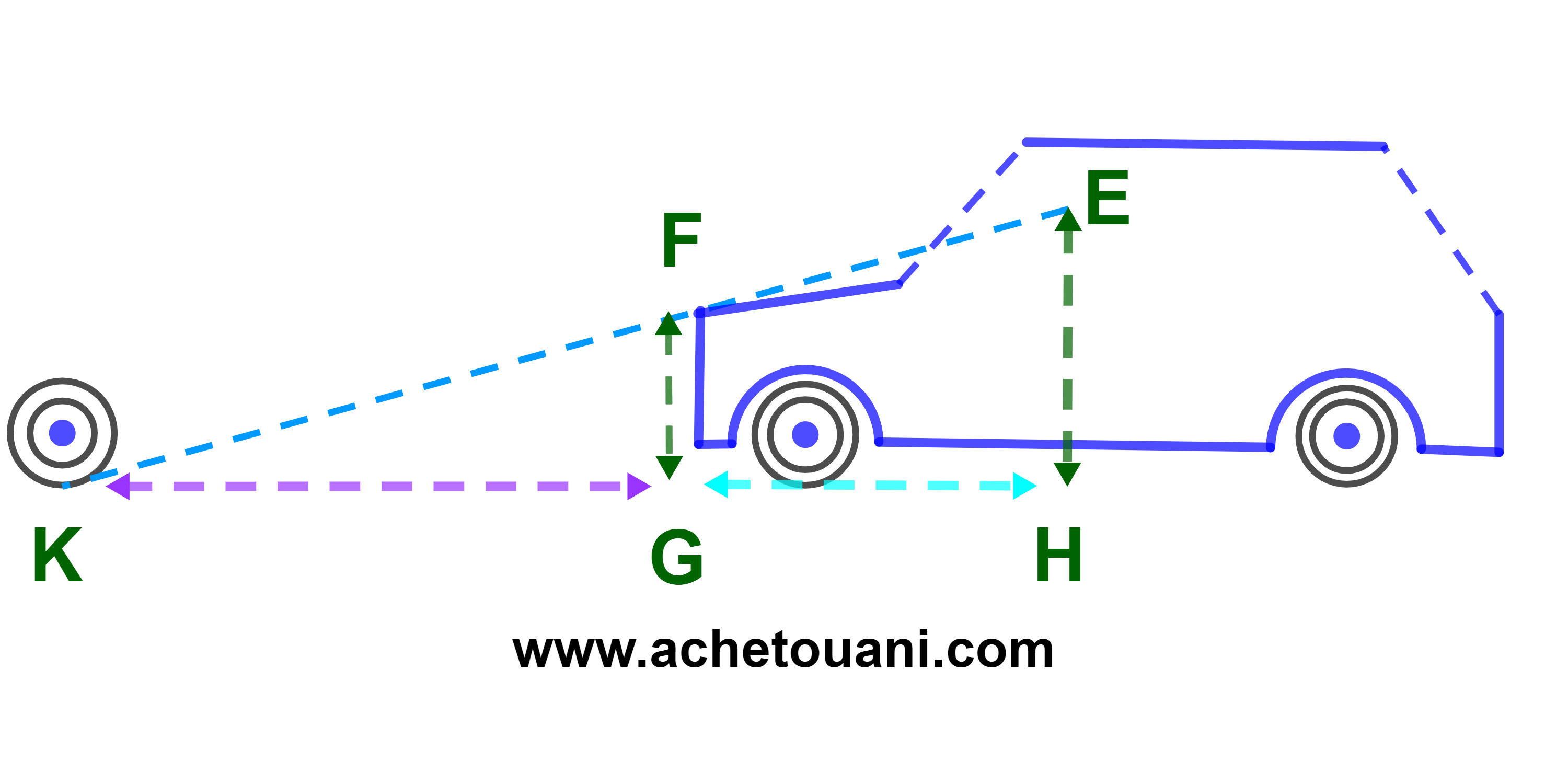
سائق سيارة يريد الوقوف وراء مركبة امامه متوقفة عند الاشارة الحمراء, وينظر الى عجلاتها الخلفية, ولما تستقيم نظرته معها بالضبط مع مقدمة سيارته يتوقف
نفترض ان الماسفة الفاصلة بين نظرته وسطح الارض تساوي EH=135cm وارتفاع مقدمة سيارته تساوي FG=80cm والمسافة الفاصلة بين مقدمة سيارته ومسقط نظرته على الارض تساوي GH=220cm
1) احسب KG المسافة الفاصلة بين مقدمة سيارته والعجلات الخلفية للسيارة المتوقفة
2) احسب tan(KG;KF).

تصحيح

1) المثلثان KFG و KEH قائمان على التوالي في G و H

tan(x) =	FG	=	EH	اذن
	KG		KH

اذن

80	=	135
KG		KG + 220

يعني 80(KG+220)=135KG
يعني 135KG-80KG=80×220
ومنه فان KG = 320.

2) قيمة مقربة للزاوية (KG;KF)

tan(x)=	FG	=	1
	KG		4

يعني tan(KG;KF)=0,25
وباستعمال آلة حاسبة tan^-1(0,25) ≃ 14,03°
ومنه فان (KG;KF) ≃ 14,03° ≃ 0,24rad.

تمرين 35 tp

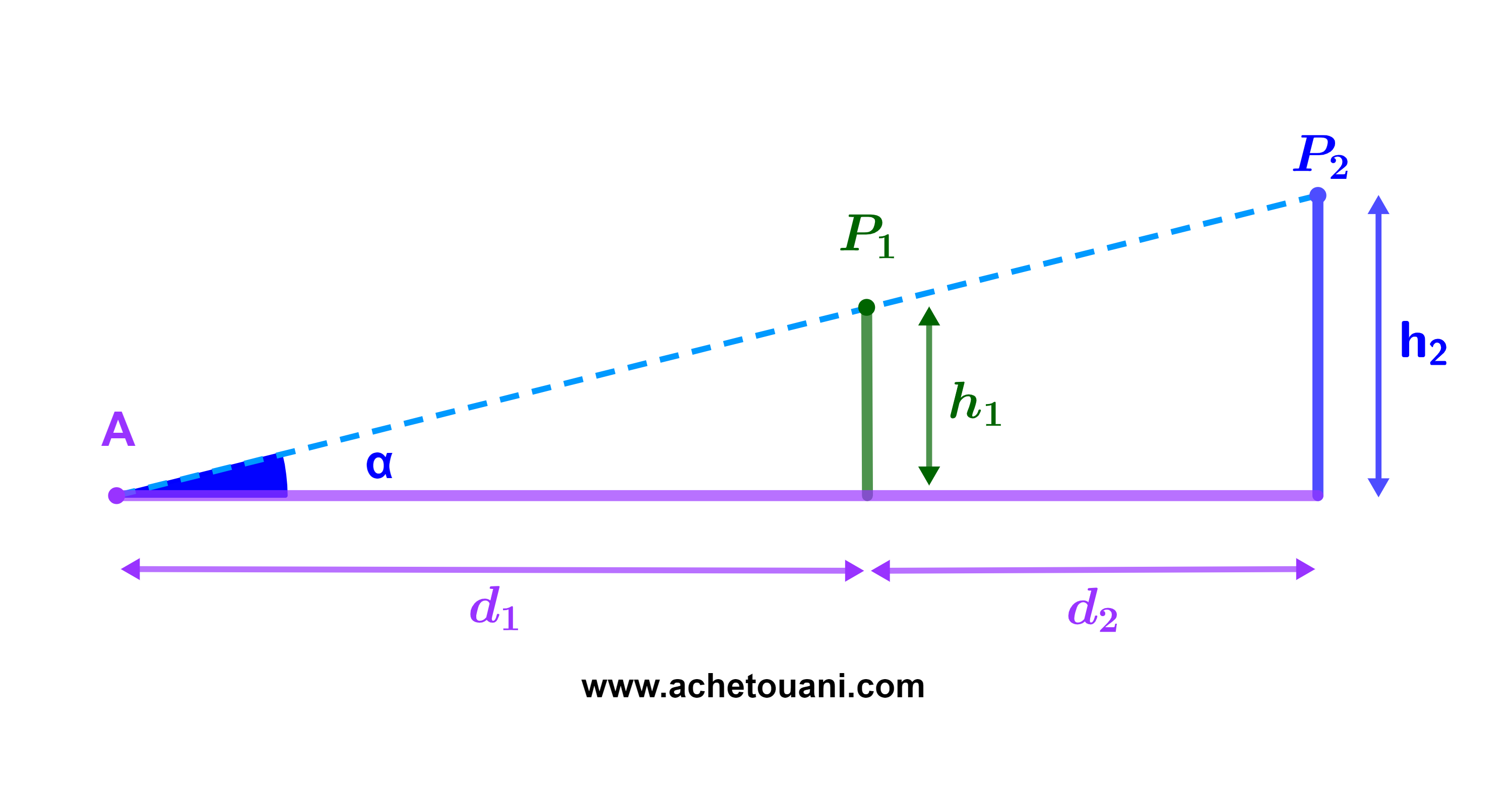
ليكن P1 و P2 عمودين كهربائيين; d2=12 مترا المسافة بينهما, ورؤوسهما ونقطة على الارض على نفس المستقيم نرمز له ب (D).
اذا كان ميل (D) هو 0,25 اي tan(α)=0,25
1) احسب d1 المسافة بين A و P1 علما ان h1=5m اتفاع P1
2) احسب h2 ارتفاع العمود P2.