تمرين 1 tp

حول ما يلي الى الراديان

20°

50°

150°

275°

تصحيح

للتذكير علاقة التحويل x و y و z على التوالي بالدرجة والراديان والغراد

x	=	y	=	z
180		π		200

اذن

الدرجة		20°		50°		270°		400°
الراديان		π		5π		3π		20π
		9		18		2		9

تمرين 2 tp

اجسب مساحة القطاع الدائري زاويته °45 من قرص شعاعه R=5 سم

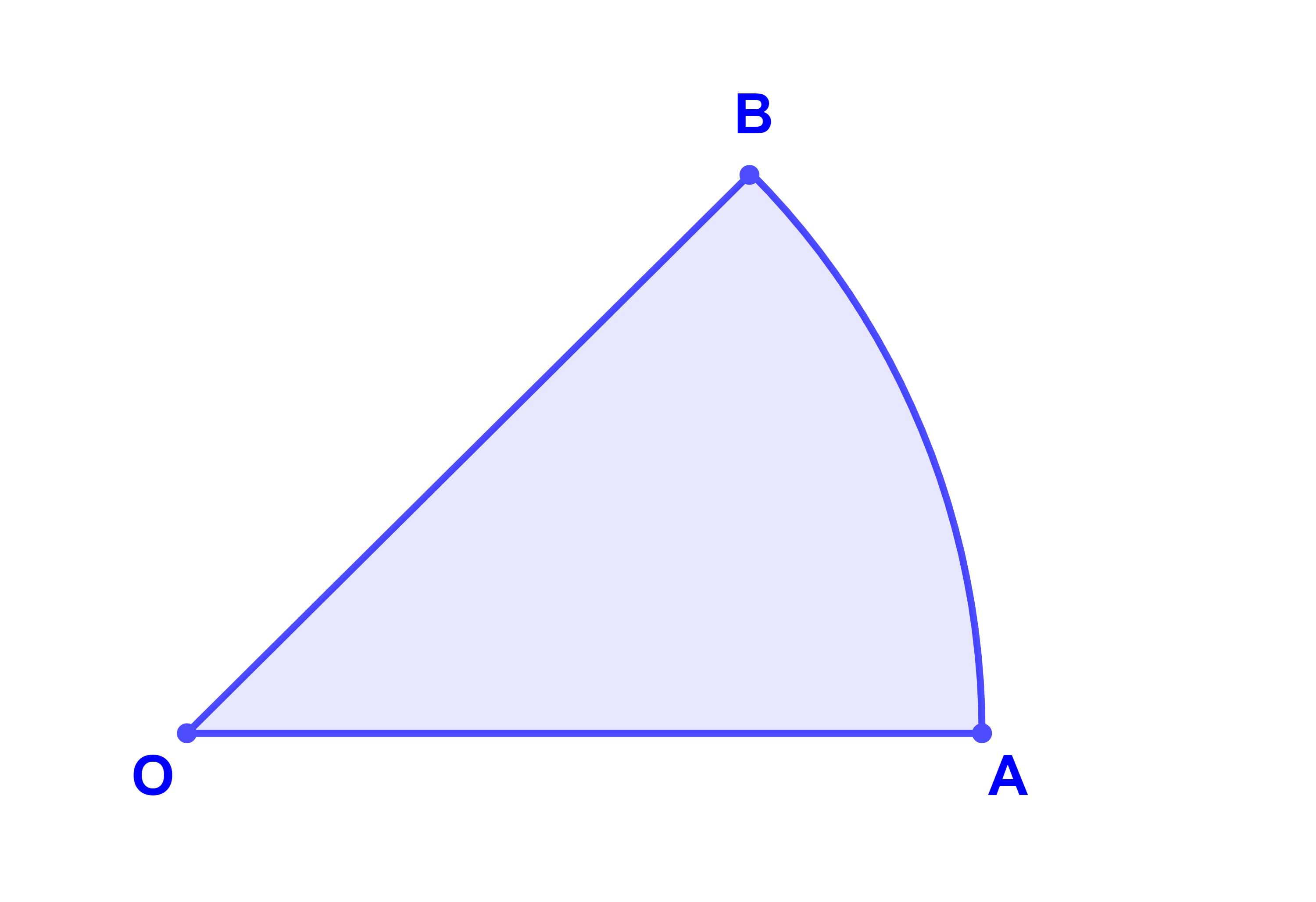
تصحيح

<> مساحة قرص شعاعه R معرفة ب A=πR²
اذا كان x قياسا بالراديان لقطاع دائري ومساحته S(x)
2π → πR²
x → S(x)
فان المساحة معرفة بالعلاقة

S(x) =	x.R²
	2

تحويل الدرجة 45° الى الراديان اذن

45° =	π	(rad)
	4

ومنه فان

S(	π	) =	π.5²	=	25π	cm²
	4		8		8

تمرين 3 tp

لتكن A و B و C ثلاث نقط من دائرة مركزها O وشعاعها R=2√(2) سم
احسب مساحة الجزء الملون المكون من القوس arc(BC)

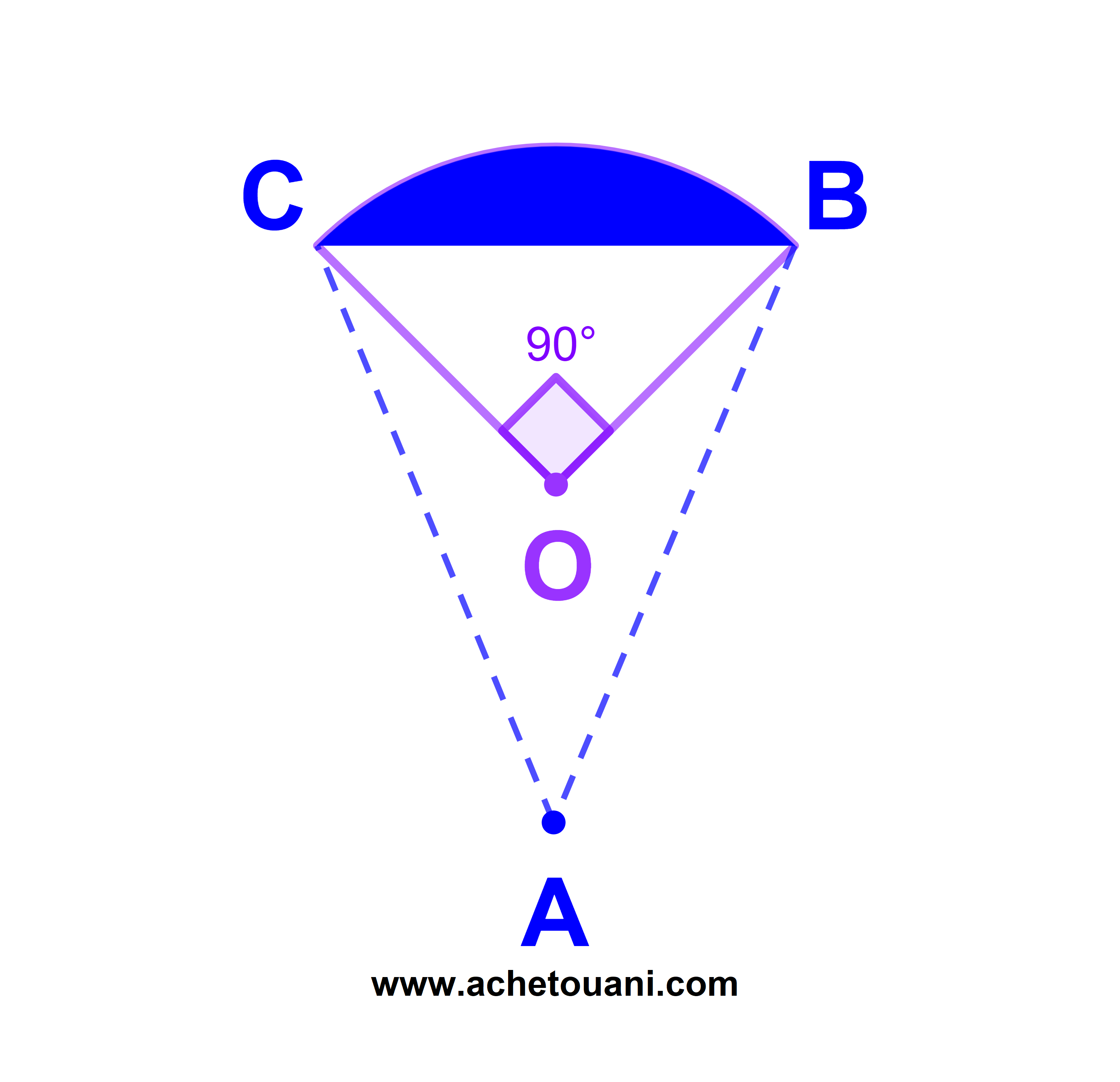
تصحيح

اولا نحسب As مساحة القطاع الدائري من القرص الذي مركزه O وشعاعه R=2√(2)
و زاوية القطاع الدائري π÷2 اذن

As(	π	) =	π.(2√(2))²	= 2π cm²
	2		4

ثم نحسب At مساحة المثلث OBC متساوي الساقين وقائم في O
اذن At=(2√(2))²÷2=4 سم مربع
وبالتالي مساحة الجز الملون المكون من القوس arc(BC)
S=As-At=(2π-4) سم مربع.