الحساب المثلثي (1_2)
تمرين 1 tp
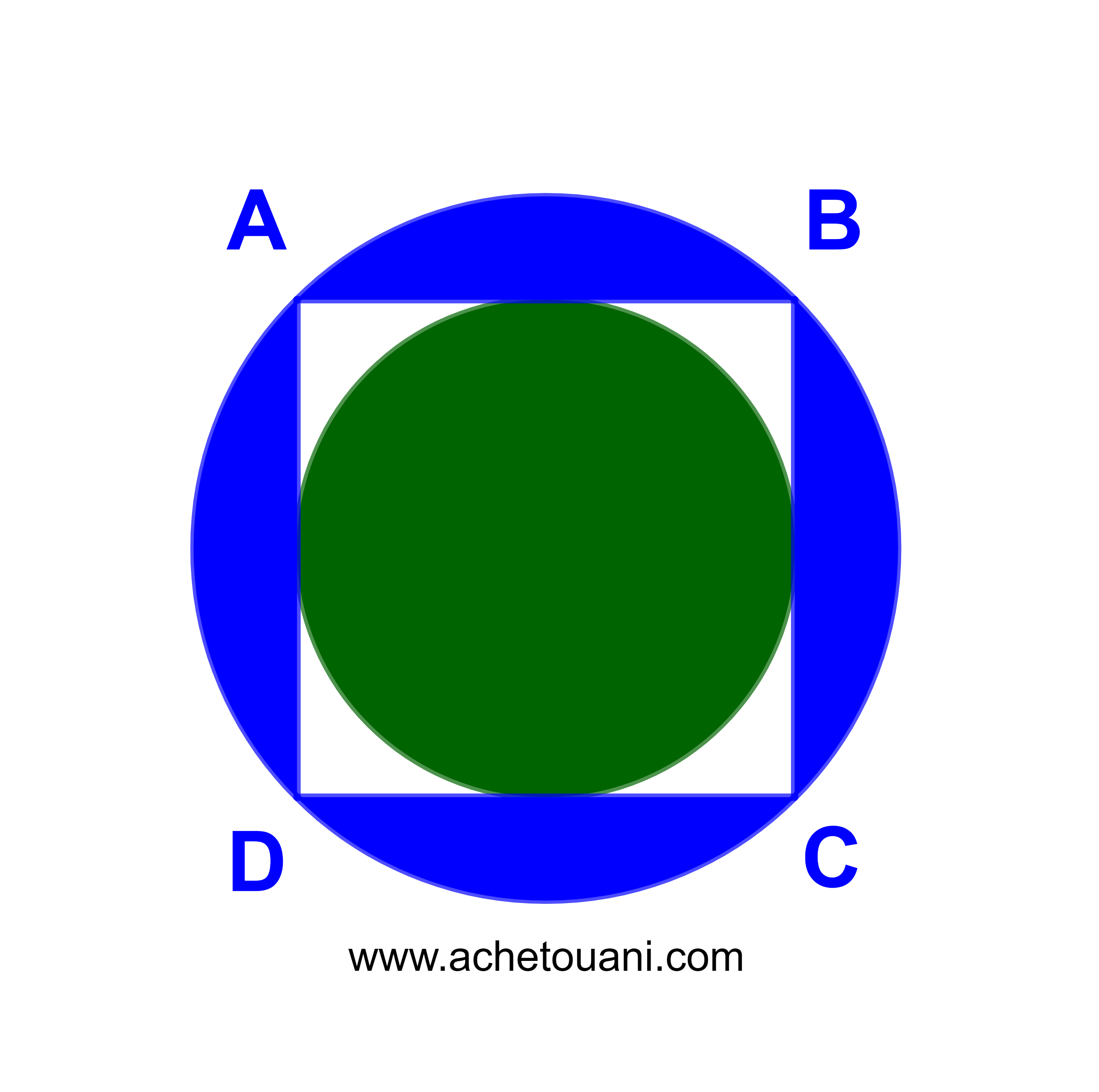
ليكن ABCD مربعا طول ضلعه AB=10 سم
1) احسب مساحة الجزء الملون بالابيض المحدد بالمربع.
2) حدد مساحة الجزء الملون بالازرق.
تصحيح
مساحة المربع ABCD
A=10×10=100 cm²
القرص الأخضر (d1) دائرته محاطة بالمربع اذن مركزه هو مركز المربع وشعاعه نصف ضلع المربع أي r=5 سم
ومنه فان مساحة القرص (d1)
A1=π×5²=25π سم مربع.
القرص الأزرق (d2) دائرته محيطة بالمربع اذن مركزه هو مركز المربع وشعاعه نصف قطر المربع أي R=5√(2)
ومنه فان مساحة القرص (d2)
A2=π×(5√(2))²
اذن A2=50π سم مربع.
1) مساحة الجزء الأبيض S1
S1=10×10-π×5²
اذن S1=(100-25π) سم مربع
2) مساحة الجزء الأزرق S2
S2=π(5√(2))²-10²
اذن S2=(50π-100) سم مربع.
تمرين 2 tp
بين ان الافاصيل المنحنية
| x = | 33π | y = | -17π | z = | 83π | |||
| 5 | 5 | 5 |
تمثل نفس النقطة M على الدائرة المثلثية التي مركزها O.
تصحيح
للتذكير
x و y يمثلان نفس النقطة على الدائرة المثلثية (C) يكافئ x≡y[2π]
وبعبارة الخرى x=y+2kπ حيث k∈ℤ
اي x و y يوافقان نفس الافصول الرئيسي.
| x - y = | 33π | - | -17π |
| 5 | 5 | ||
| = | 50π | = 2.25π | / (k=25) |
| 5 |
اذن x=y+2kπ مع k=25∈ℤ ومنه فان x و y يمثلان نفس النقطة على الدائرة المثلثية (C).
| x - z = | 33π | - | 83π |
| 5 | 5 | ||
| = | -50π | = 2.(-5)π | / (k=-5) |
| 5 |
اذن x≡z[2π]
ومنه فان y≡z[2π]
وبالتالي x و y و z تمثل نفس النقطة على الدائرة المثلثية (C).
تمرين 3 tp
بين ان الأفاصيل المنحنية التالية
| x = | 99π | y = | - 213π | z = | 59π | |||
| 4 | 4 | 4 |
تمثل نفس النقطة M على الدائرة المثلثية التي مركزها O.
تمرين 4 tp
حدد من بين الافاصيل المنحنية التالية التي تمثل نفس النقطة على الدائرة المثلثية
| x = | 53π | y = | 77π | z = | - 115π | |||
| 8 | 8 | 8 |