Calcul trigonométrique (1_1)
Exercice 1 tp
Convertir en radians
| 20° | 50° | 150° | 275° |
Correction
Rappel Relation de conversion
Soient x; y et z des mesures respectives en dégré ; radians et grade.
| x | = | y | = | z |
| 180 | π | 200 |
Ainsi
| Degré | 20° | 50° | 270° | 400° | ||||
| Radians | π | 5π | 3π | 20π | ||||
| 9 | 18 | 2 | 9 |
Exercice 2 tp
Calculer l'aire du secteur circulaire d'angle 45° d'un disque de rayon R=5 cm.
Correction
A=πR² est l'aire d'un disque de rayon R.
Soit x la mesure d'angle en radian d'un secteur
En utilisant la proportionnalité ou la régle de trois
2π → πR²
x → S(x)
on obtient la relation qui définit l'aire
| S(x) = | x.R² |
| 2 |
Convertion de 45° en radians
| 45° = | π | (rad) |
| 4 |
ainsi
| S( | π | ) = | π.5² | = | 25π | cm² |
| 4 | 8 | 8 |
Exercice 3 tp
Soient A ; B et C trois points d'un cercle de centre O et de rayon R=2√(2)cm .
Calculer l'aire de la partie colorée formée par l'arc(BC).
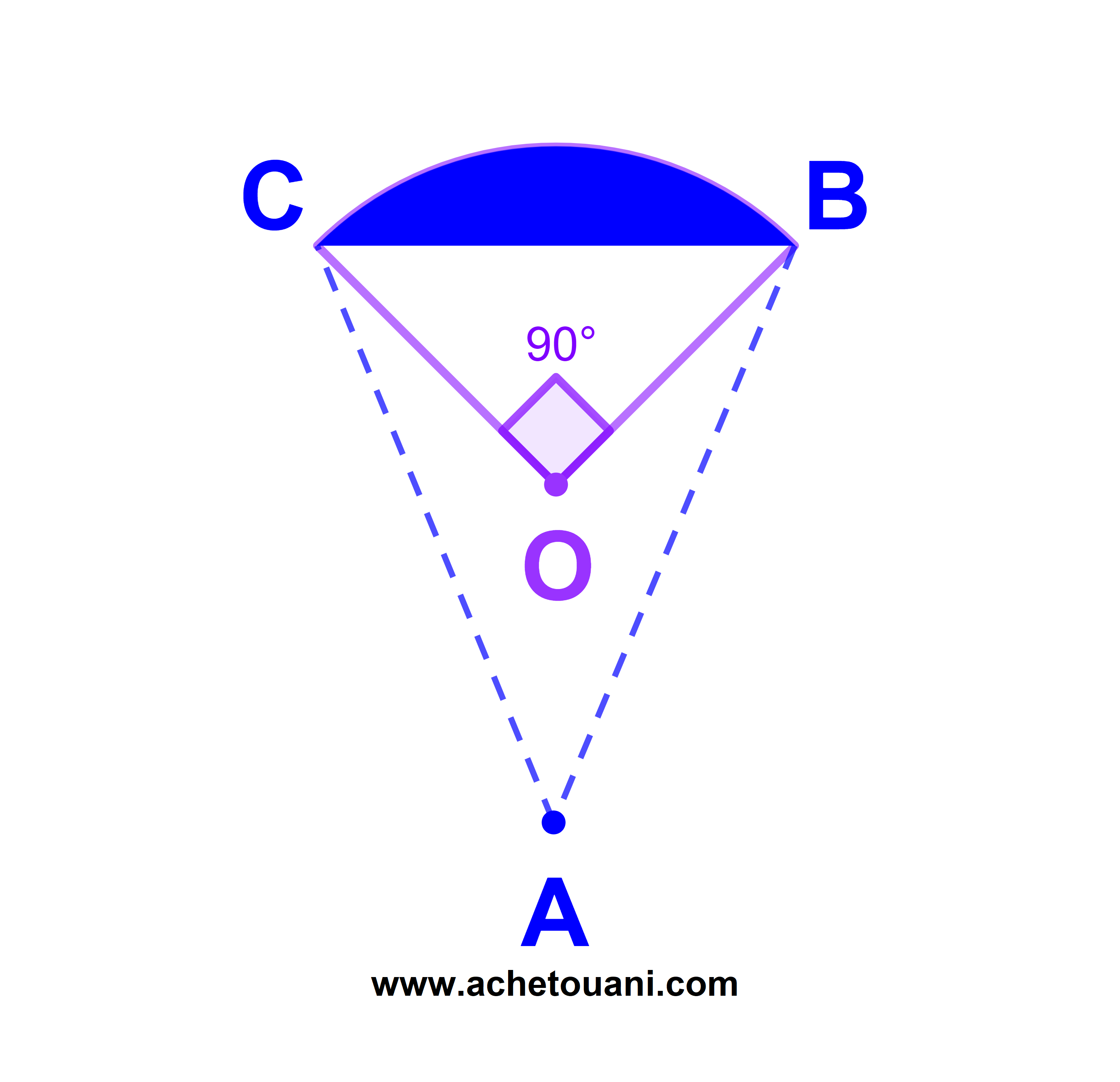
Correction
On calcule d'abord As l'aire du secteur d'un disque de centre O et de rayon R=2√(2).
π÷2 est la mesure de l'angle du secteur circulaire
| As( | π | ) = | π.(2√(2))² | = 2π cm² |
| 2 | 4 |
Puis on calcule At l'aire du triangle OBC.
(OBC est isocèle et rectangle en O)
donc At=(2√(2))²÷2=4cm²
ainsi l'aire de la partie colorée formée par l'arc(BC)
S=As - At=(2π-4) cm².