Exercice 1 tp

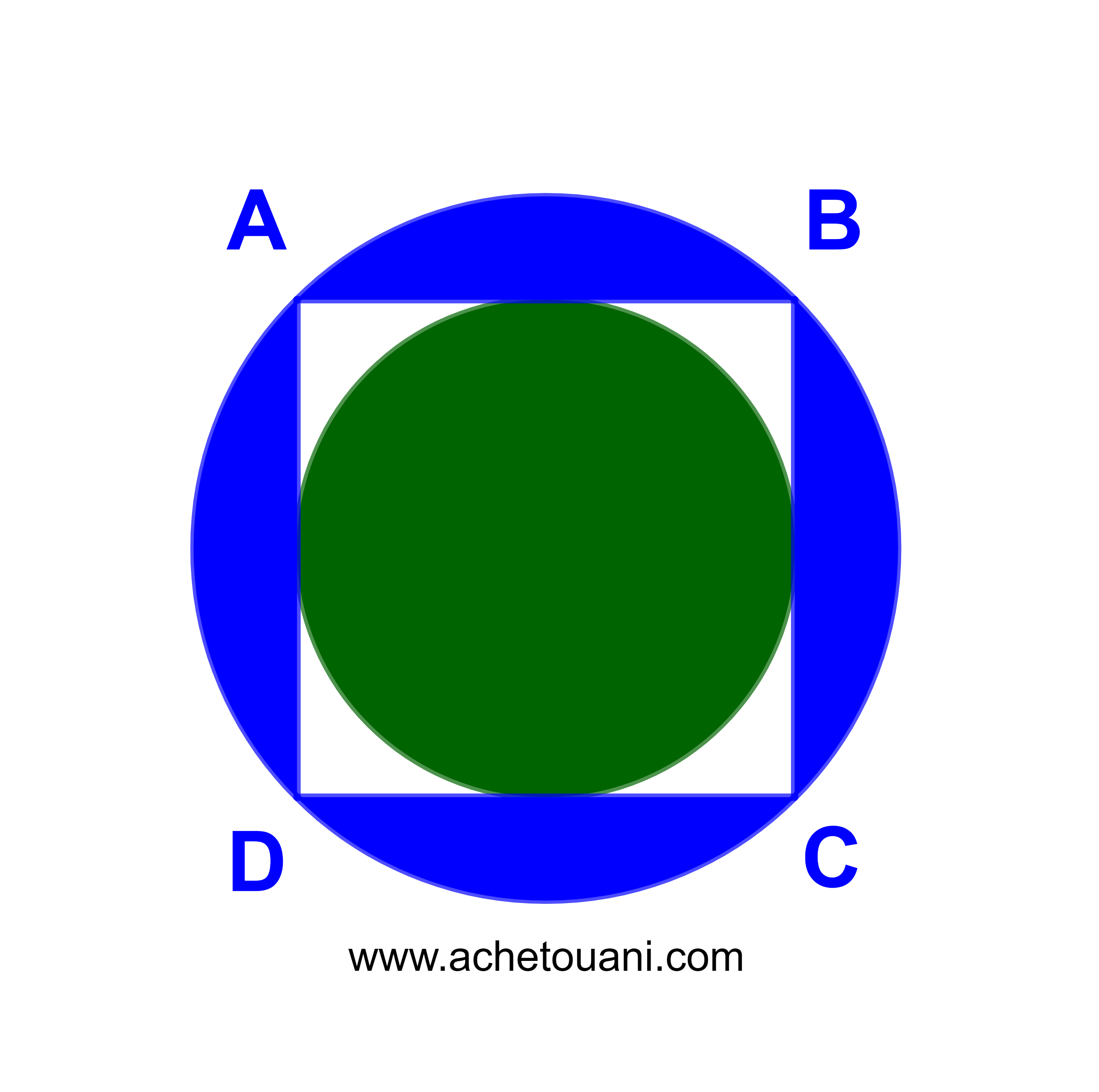
Soit ABCD un carré de coté AB=10 cm.
1) Calculer l'aire de la partie blanche délimitée par le carré.

2) Calculer l'aire de la partie colorée en bleu.

Correction

L'aire du carré ABCD
A=10×10=100 cm².
Le périmètre du disque blanc (C1) est un cercle inscrit au carré
donc son centre est le centre du carré et son rayon est la moitié du coté du carré.
r=5 cm ainsi l'aire de (C1)
A1=π×5²= 25πcm².
Le périmètre du disque blue (C2) est un cercle circonscrit au carré.

Le centre du disque (C2) est le centre du carré et le rayon est la moitié de la diagonale du carré.
R=5√(2) ainsi l'aire de (C2)
A2=π×(5√(2))²=50πcm².
1) L'aire de la partie blanche S1
S1=10×10 - π×5²
donc S1=(100 - 25π) cm²
2) L'aire de la partie bleue َS2
S2=π(5√(2))² - 10²
donc S2=(50π - 100) cm²

Exercice 2 tp

Montrer que les abscisses curvilines suivantes

x =	33π		y =	-17π		z =	83π
	5			5			5

représentent le même point M sur le cercle trigonométrique de centre O.

Correction

Rappel
x et y représentent le même point sur le cercle trigonométrique (C) équivaut x≡y[2π].
équivaut x=y+2kπ tel que k∈ℤ
équivaut x et y ont la même abscisse principale.

x - y =	33π	-	-17π
	5		5
=	50π	= 2.25π	(k=25)
	5

Donc x=y+2kπ tel que k=25∈ℤ
ainsi x et y représentent le même point sur (C).

x - z =	33π	-	83π
	5		5
=	-50π	= 2.(-5)π	(k=-5)
	5

donc x≡z[2π]
et puisque x≡y[2π] alors y≡z[2π]
ainsi x ; y et z représentent le même point sur (C).

Exercice 3 tp

Montrer que les abscisses curvilines suivantes

x =	99π		y =	- 213π		z =	59π
	4			4			4

représentent le même point M sur le cercle trigonométrique de centre O.

Exercice 4 tp

Déterminer parmi les abscisses curvilines suivantes qui représentent le même point sur le cercle trigonométrique de centre O.

x =	53π		y =	77π		z =	- 115π
	8			8			8