3.3 L'inéquation tanx ≥ a

3.3.1 Exemple

Résoudre dans I=[-π;π] l'inéquation
tanx≥-√3 et déduire l'ensemble des solutions de l'inéquation tanx<-√3 sur I.

Correction

Notons que tanx∈IR si

x∈IR\{	π	+ kπ tel que k∈ℤ}
	2

Soit x∈I=[-π;π]. tanx∈IR si

x≠	-π	et x≠	π
	2		2

1) On résout l'équation
(E): tanx = -√3 dans IR

tan(	-π	) = - tan(	π	)= - √3
	3		3

Donc (E) signifie

tanx = tan(	-π	)
	3

signifie

x =	-π	+ kπ tel que k∈ℤ
	3

2) On encadre ces solutions
sur I=[-π;π].

-π≤	-π	+kπ	≤π
	3

Signifie

-1≤	-1	+k	≤1
	3

signifie

-1-	-1	≤+k≤1-	-1
	3		3

signifie

-2	≤k≤	4
3		3

k∈ℤ donc k=0 ou k=1 ainsi

x =	-π	ou x =	2π
	3		3

Ces deux solutions sont toutes les deux différentes de

-π	et	π
2		2

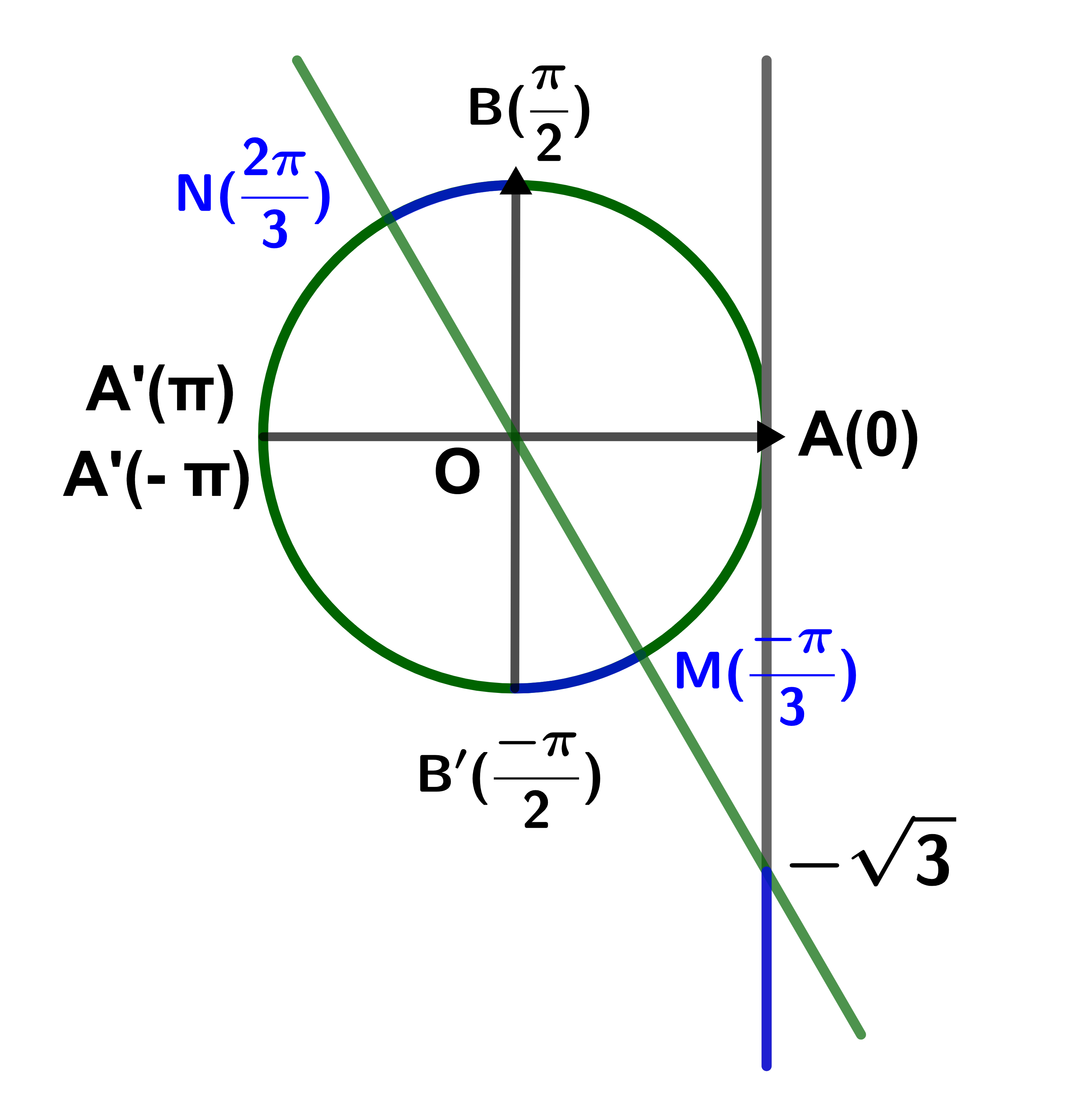
3) On représente les solutions sur un axe ou sur le cercle trigonométrique (C).
(-π)---(-π/2)---(-π/3)---(0)
(0)---(π/2)---(2π/3)---(π)
alors l'ensemble de solutions de l'inéquation
S =

[-π;	-π	[ ∪ [	-π	;	π	[∪[	2π	;π]
	2		3		2		3

L'ensemble des solutions de l'inéquation
tanx<-√3 sur I en utilisant le résultat de précédent

(-π)---(-π/2)---(-π/3)---(0)
(0)---(π/2)---(2π/3)---(π)

S = ]	-π	;	-π	[∪]	π	;	2π	[
	2		3		2		3