4- Les angles inscrits et les quadrilatères inscriptibles

4.1 angle inscrit et angle au centre

4.1.1 Activité

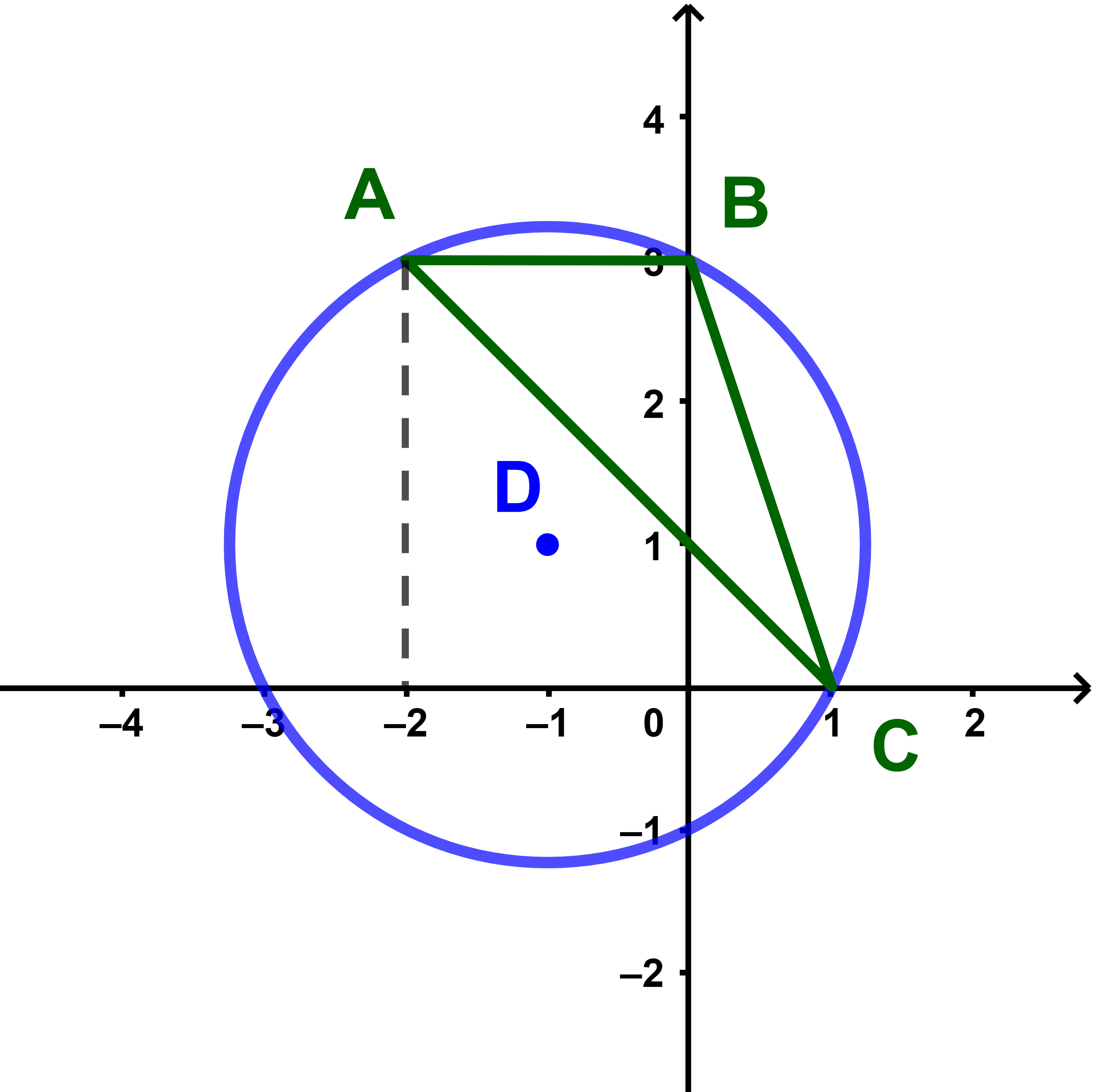
Le plan ℙ est rapporté à un repère orthonormé (O;i^→;j^→). On considère dans ℙ les points A(-2;3); B(0;3); C(1;0) et D(-1;1).
1) Représenter ces points dans le repère.
2) Montrer que D est le centre du cercle circonscrit au triangle (ABC).
3) Quelle est la nature du triangle (DBC)?

4) Calculer la mesure de l'angle (AC;AB)?

4.1.2 Définitions

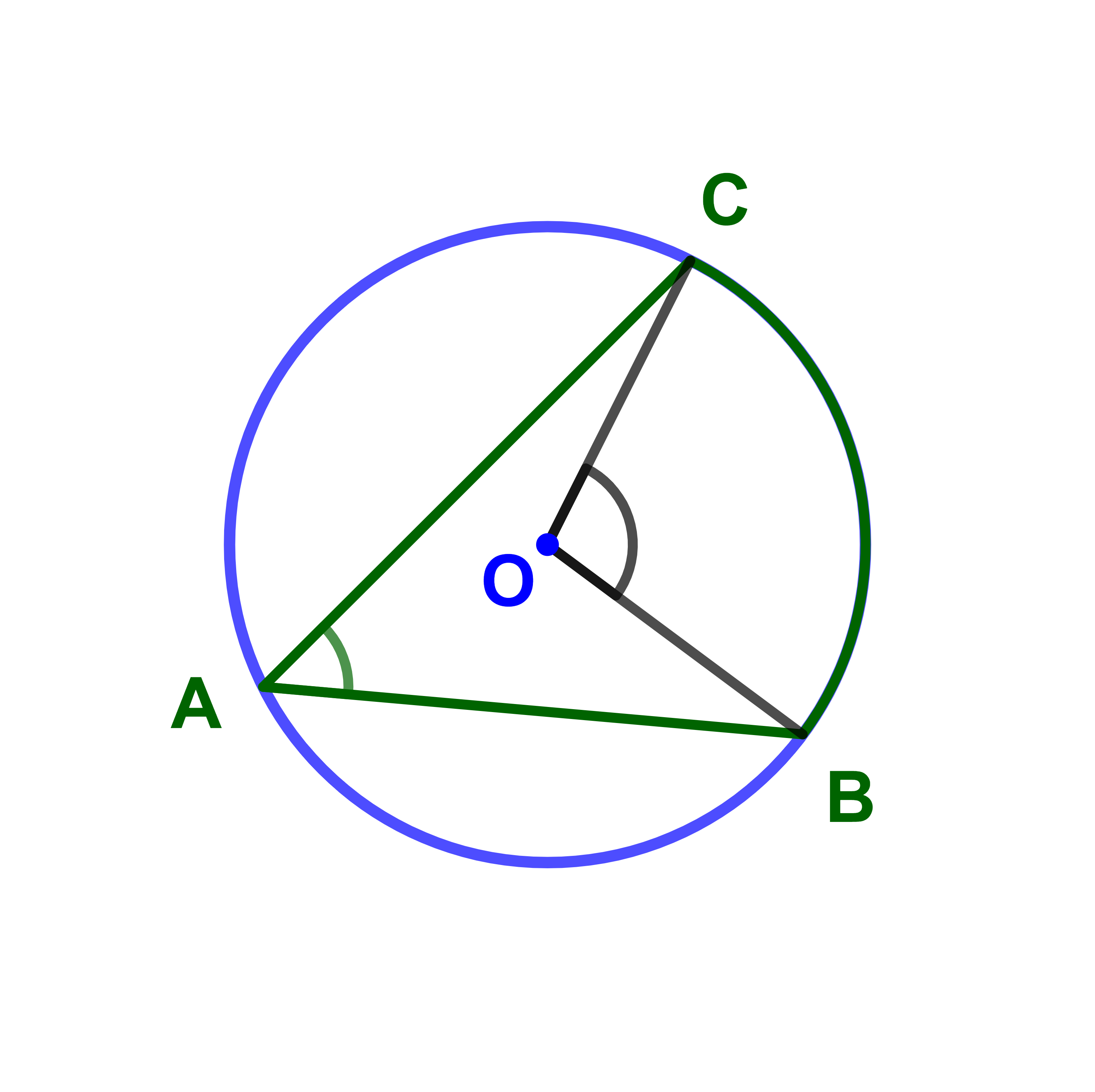
Soient A ; B et C trois points d'un cercle de centre O.
1) L'angle (AB;AC) est appelé angle inscrit.
2) L'angle (OB;OC) est appelé angle au centre.

4.1.3 Propriété

Soient B et C deux points d'un cercle de centre O et A un point du cercle différent de B et C.
(OB;OC)=2(AB;AC)+2kπ tel que k∈ℤ.

4.3 Angles interceptant le même arc

4.3.1 Théorèmes

1) Deux angles inscrits dans un cercle interceptant le même arc du cercle sont de même mesure.

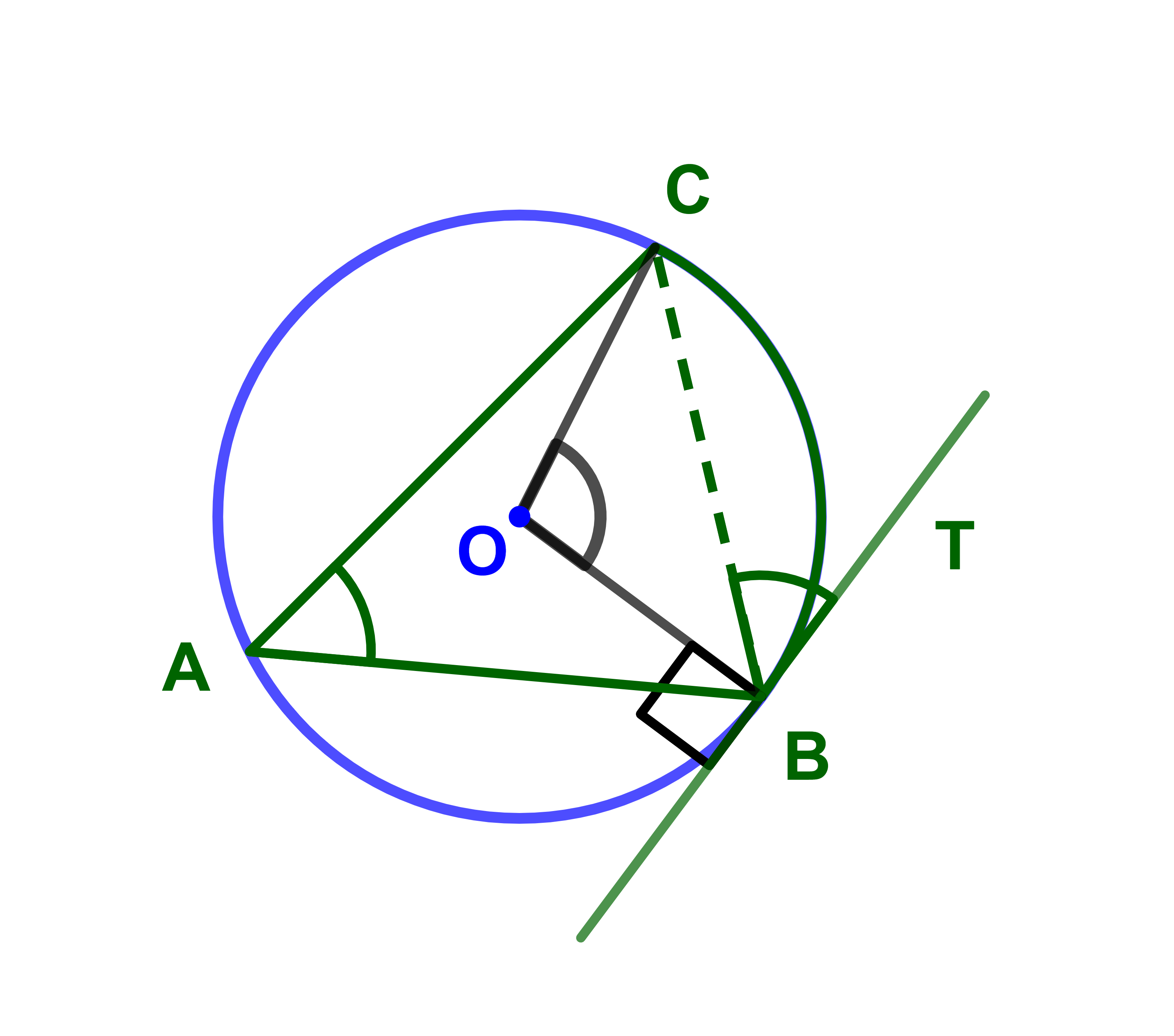
2) Soient A ; B et C des points d'un cercle de centre O tels que A≠B et A≠C.
L'angle inscrit (AB;AC) est de même mesure que l'angle (BT;BC ) formé par la demi-tangente [BT) et la corde [BC].

Remarque
L'angle (AB;AC) et l'angle (BT;BC) interceptent le même arc.

4.3.2 Propriétés

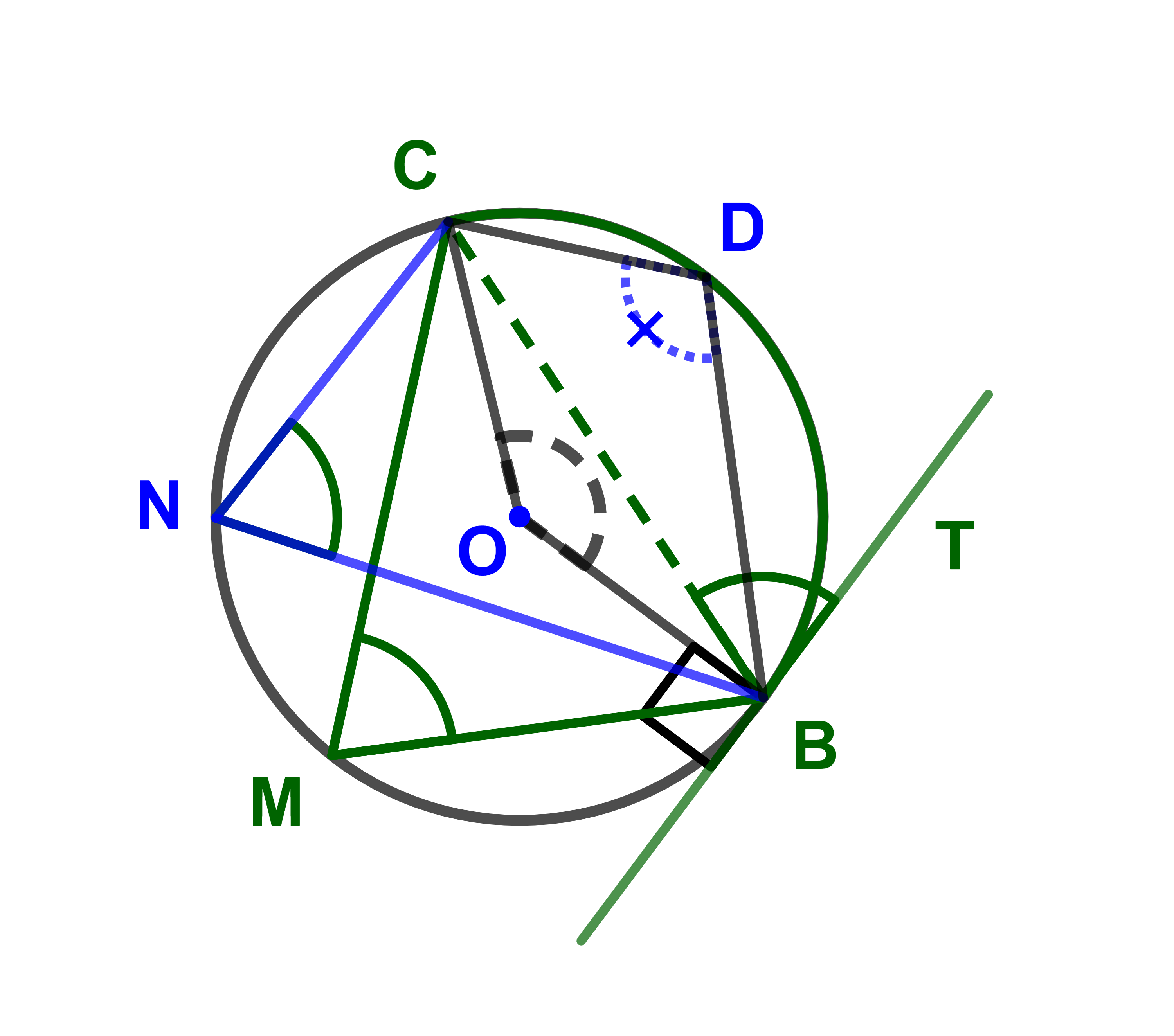
Soient B; C et D trois points d'un cercle de centre O. Pour tous points M et N de l'arc [BC] qui ne contient pas le point D et T un point de la tangente au cercle passant par B.
1) (MB;MC)=(BT;BC)=(NB;NC)+2kπ.
2) (MB;MC)+(DB;DC) = π+2kπ (k∈ℤ).

4.3.3 Définition

M ; B ; D et C sont quatre points cocyclique s'ils se trouvent sur le même cercle.

4.3.4 Propriété

M ; B ; D et C sont cocyclique signifie (MB;MC)+(DC;DB)=π+2kπ (k∈ℤ).