4- الزوايا المحيطية و الرباعيات الدائرية

4.1 الزاوية المركزية والزاوية المحيطية

4.1.1 أنشطة

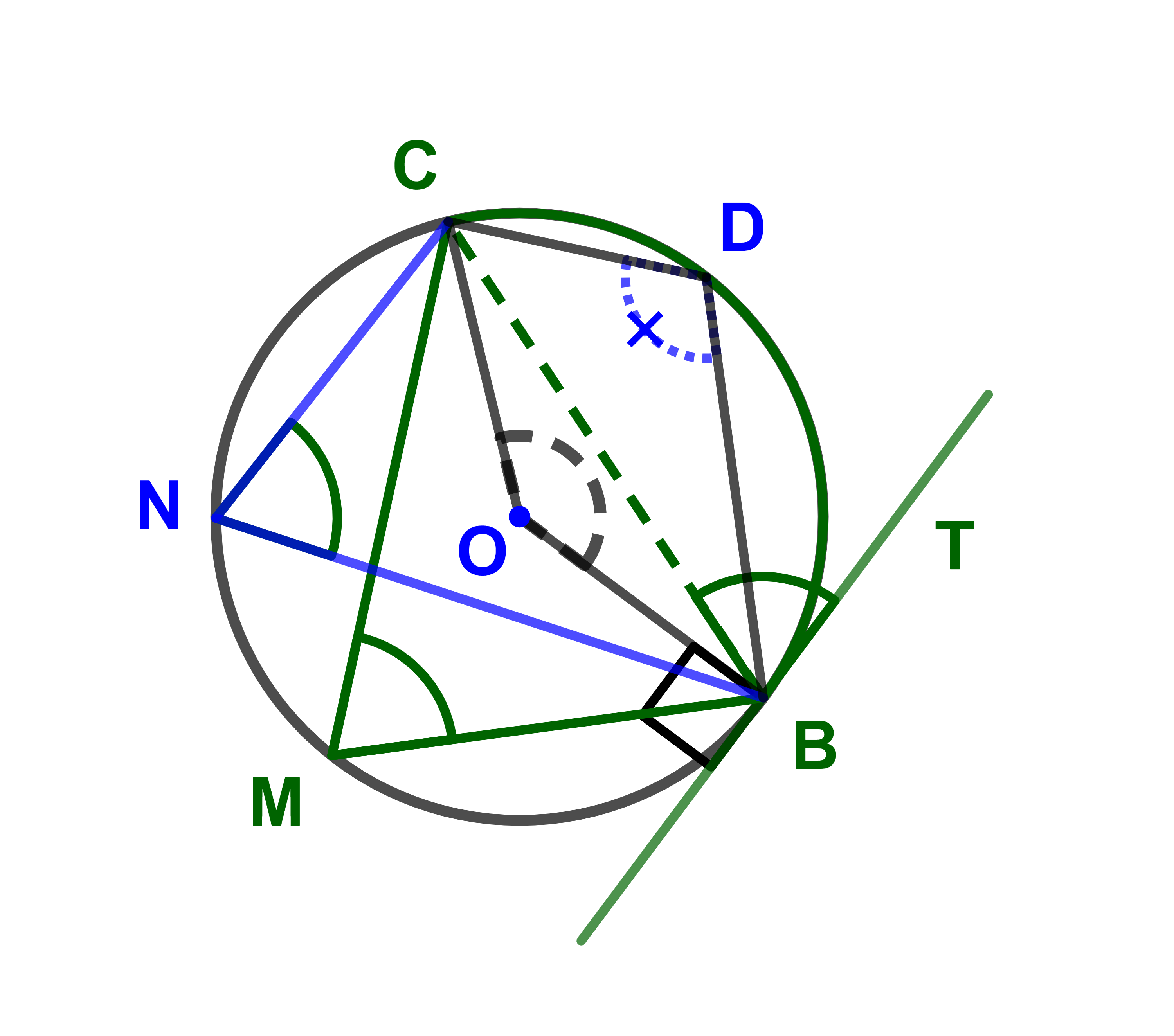
المستوى منسوب الى معلم متعامد ممنظم (O;i^→;j^→). نعتبر في ℙ النقط A(-2;3) و B(0;3) و C(1;0) و D(-1;1).
1) مثل النقط A و B و C و D.
2) بين أن D مركز الدائرة المحيطة بالمثلث (ABC).
3) ما هي طبيعة المثلث (DBC) ?
4) ما هو قياس الزاوية (AC;AB) ?

4.1.2 تعاريف

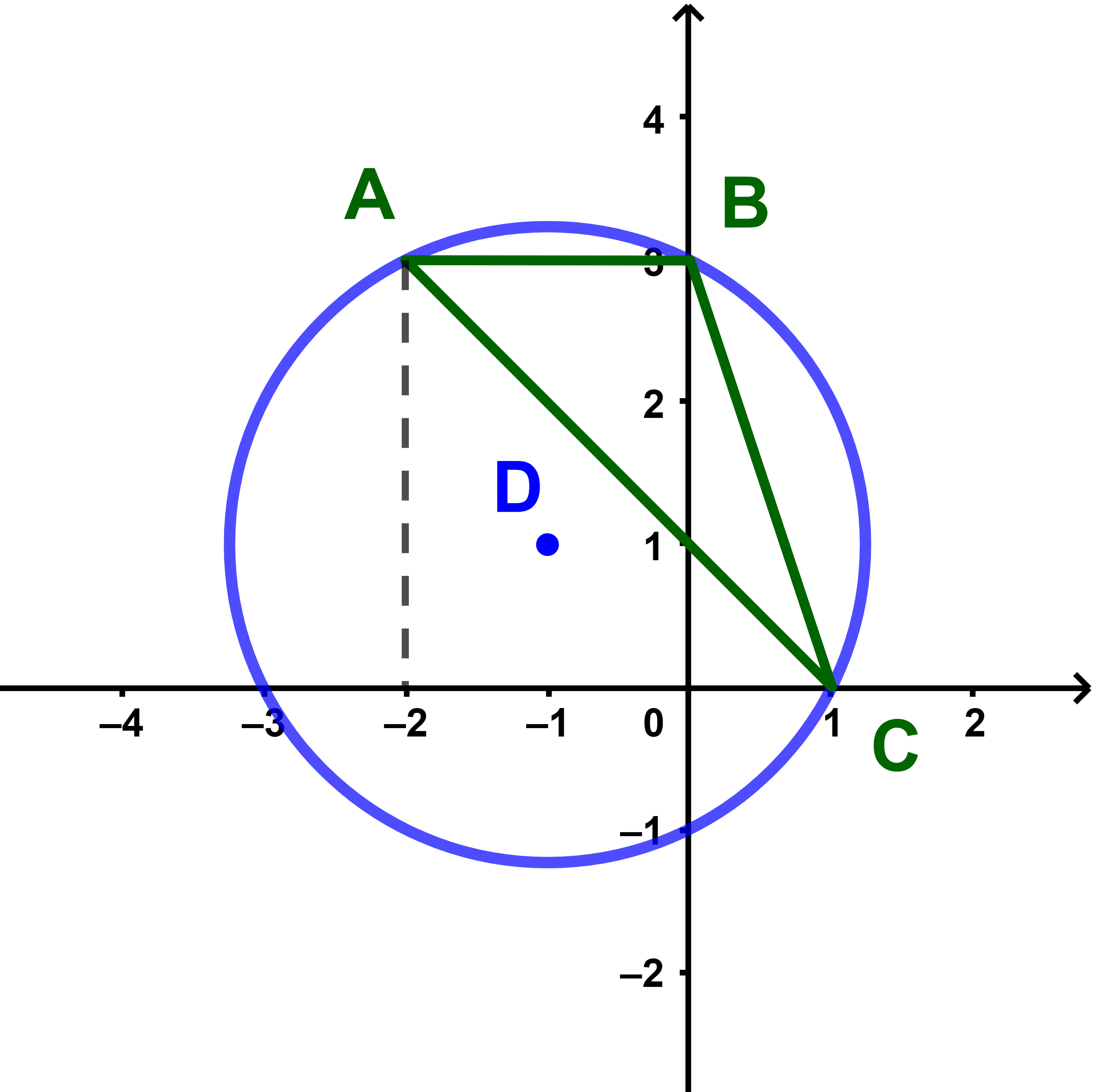
لتكن A و B و C ثلاث نقط من دائرة مركزها O.
1) الزاوية (AB ; AC) تسمى زاوية محيطية.
2) الزاوية (OB ; OC) تسمى زاوية مركزية.

4.1.3 خاصية

لتكن B و C نقطتين من دائرة مركزها O.
لكل نقطة A من الدائرة ومخالفة ل B و C.
لدينا (OB;OC)= 2(AB;AC)+2kπ حيث k∈ℤ.

4.3 زوايا تحصر نفس القوس في دائرة

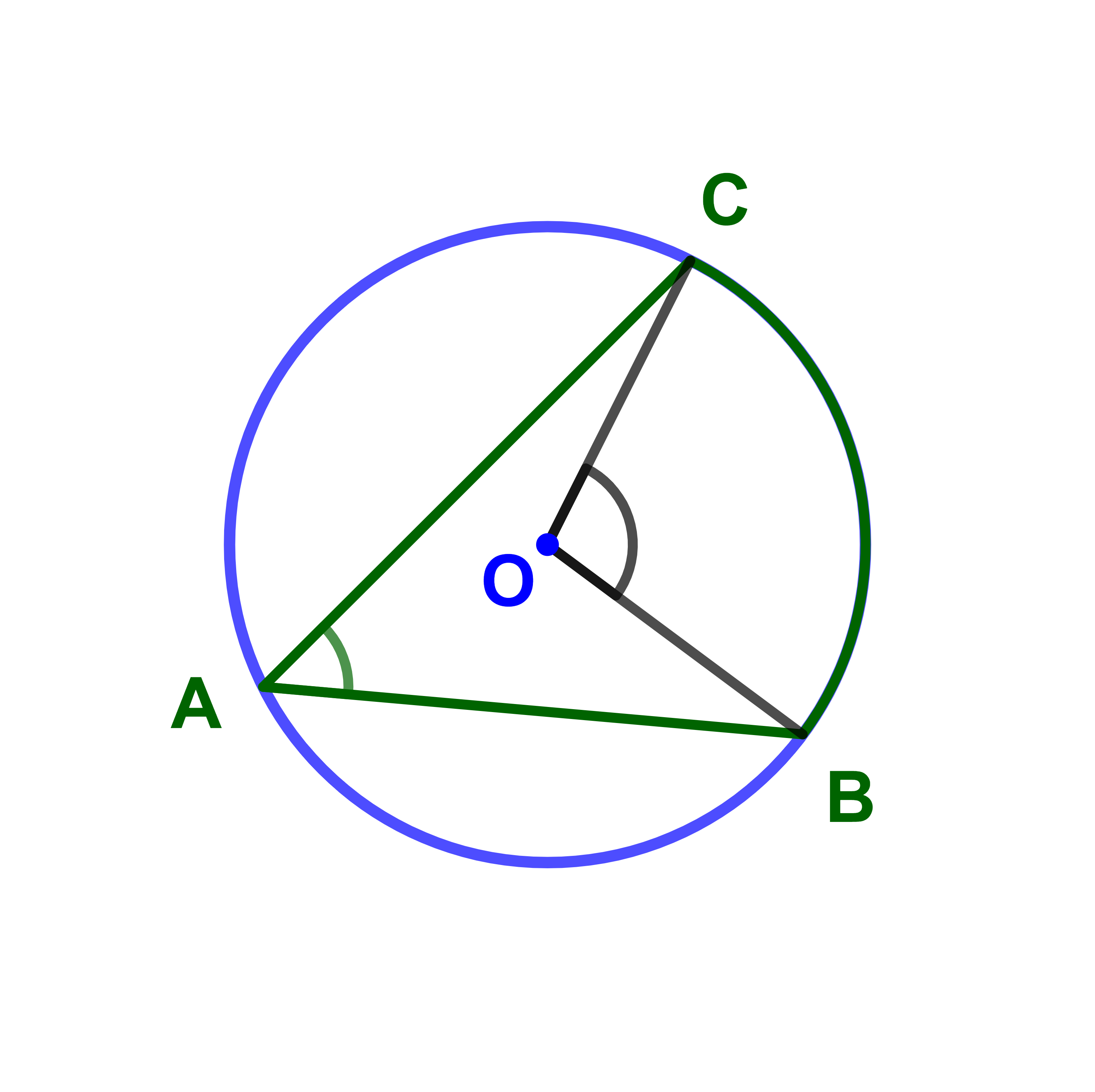
4.3.1 مبرهنة 1

زاويتان محيطيتان في دائرة وتحصران نفس القوس لهما نفس القياس.

4.3.2 مبرهنة 2

لتكن A و B و C نقطا من دائرة مركزها O حيث A≠B و A≠C.
الزاوية المحيطية (AB;AC) لها نفس قياس الزاوية (BC;BT) المحددة من نصف المماس [BT) و [BC].

ملاحظة
الزاويتان (AB;AC) و (BT;BC) تحصران نفس القوس.

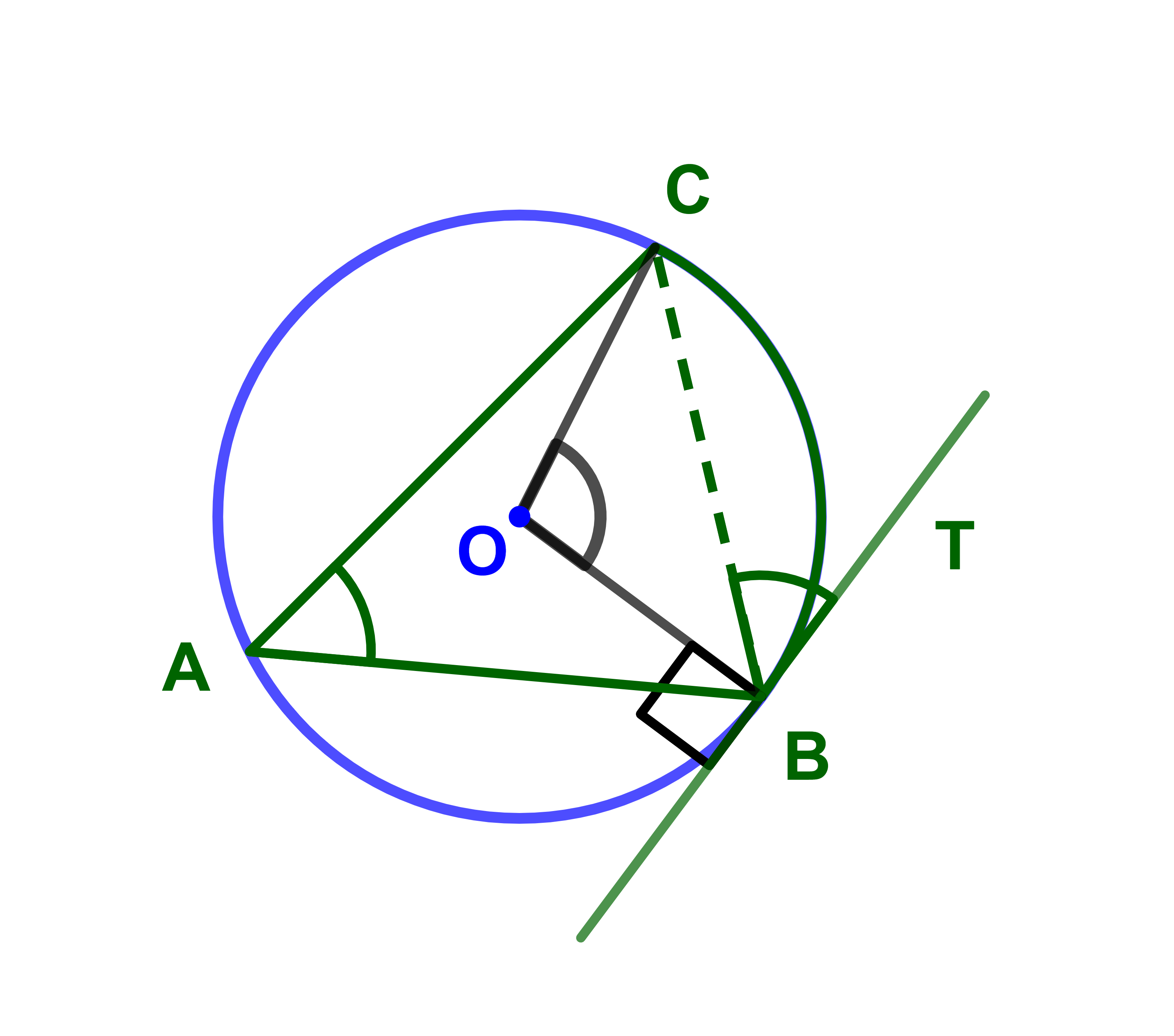
4.3.3 خاصيات

لتكن B و C و D ثلاث نقط من دائرة مركزها O و M و N نقطتين من القوس [BC] الذي لا يحتوي على D
و T نقطة من مماس الدائرة والمار من B.
لدينا 1) (MB;MC)=(BT;BC)=(NB;NC)+2kπ
2) (MB;MC)+(DB;DC) = π +2kπ بحيث k∈ℤ.

4.3.4 تعريف

نقول ان أربع نقط M و B و D و C حلقية اذا كانت تنتمي الى نفس الدائرة.

4.3.5 خاصية

M و B و D و C أربع نقط حلقية يعني
(MB;MC)+(DC;DB)=π+2kπ حيث (k∈ℤ).