الحساب المثلثي (2_12)
5- العلاقات المثلثية في مثلث
5.1 خاصية
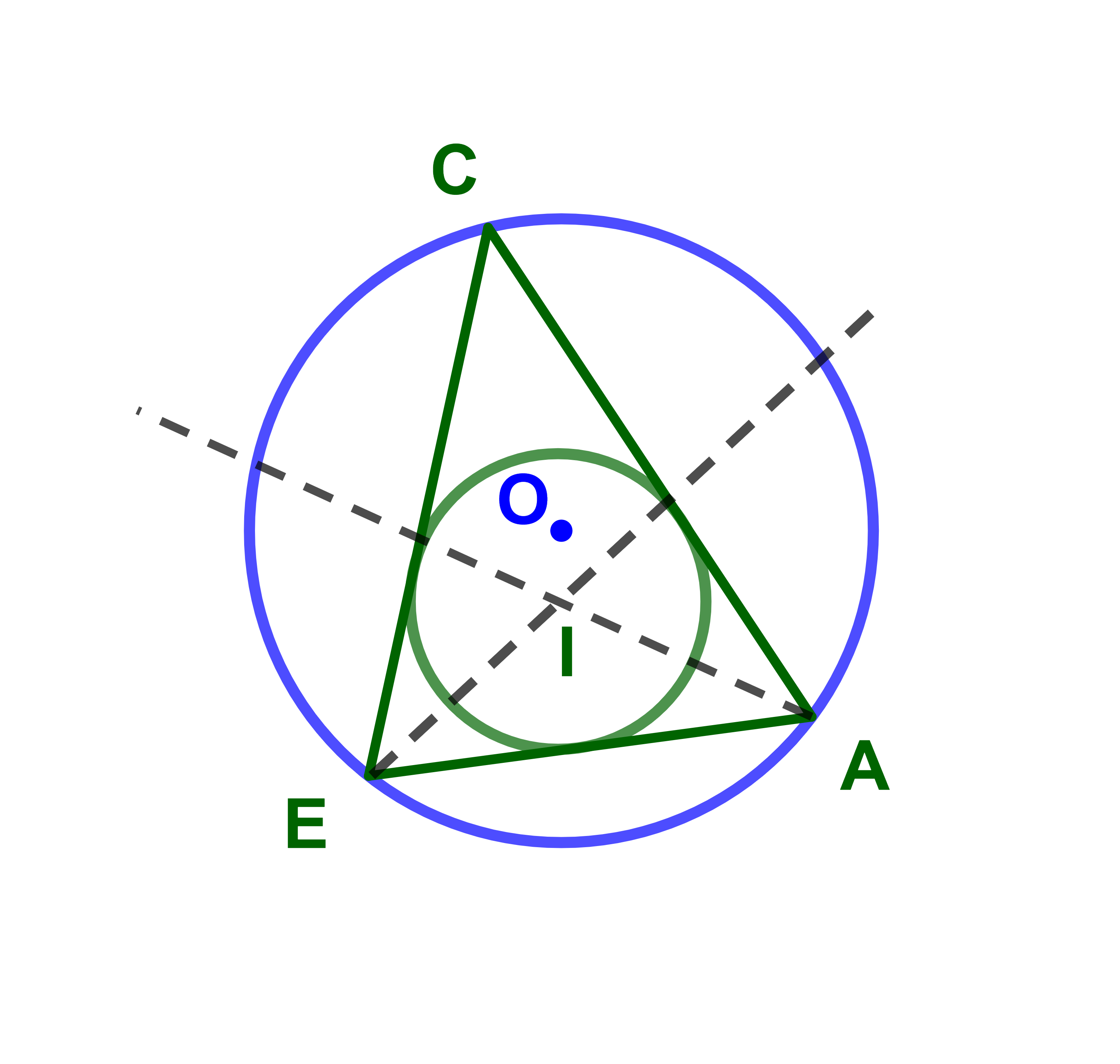
ليكن (AEC) مثلثا.
r شعاع الدائرة المحاطة بالمثلث (EAC) و
R شعاع الدائرة المحيطة بالمثلث (EAC).
نضع EA=c و EC=a و AC=e. لدينا
| a | = | e | = | c | = | 2R |
| sin(Â) | sin(Ê) | sin(Ĉ) |
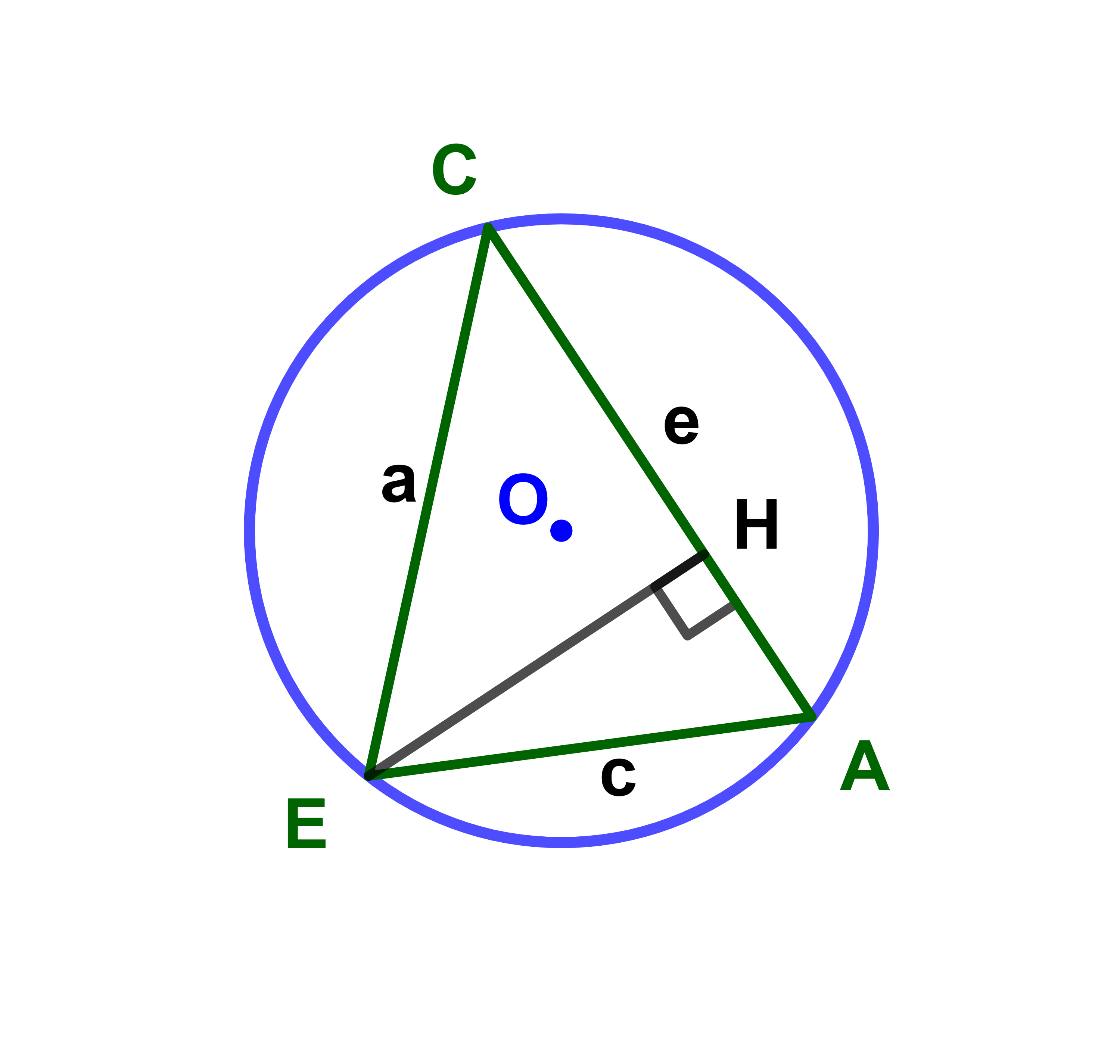
برهان
1) لتكن النقطة H المسقط العمودي للنقطة E على المستقيم (BC).
المثلثان AHE و HCE قائما الزاوية في النقطة H اذن
| sinĈ = | HE | و | sin = | HE |
| a | c |
ومنه فان
c.sin Â=a.sinĈ
أي
| a | = | b |
| sin | sinĈ |
بنفس الطريقة نبين أن
| a | = | e |
| sin | sinÊ |
ومنه فان
| a | = | e | = | c |
| sin | sinÊ | sinĈ |
2) نعتبر المثلث المتساوي الساقين OEC
نعلم أن (OE;OC)=2(AE;AC)
اذن
| (EA;EO) = | π | -Ā |
| 2 |
لدينا
| cos(EA;EO) = | a/2 |
| R |
اذن
| sinĀ = | a |
| 2R |
ومنه فان
| 2R = | a |
| sinĀ |
5.2 مساحة ثلث
5.2.1 خاصية 1
مساحة مثلث EAC معرفة بما يلي
| S = | 1 | acsinÊ |
| 2 |
بحيث EA=c و EC=a و AC=e.
5.2.2 خاصية 2
مساحة مثلث EAC معرفة بما يلي S=pr
حيث p محيطه و r شعاع الدائرة المحاطة به.