5- Relations trigonométriques dans un triangle

5.1 Propriété

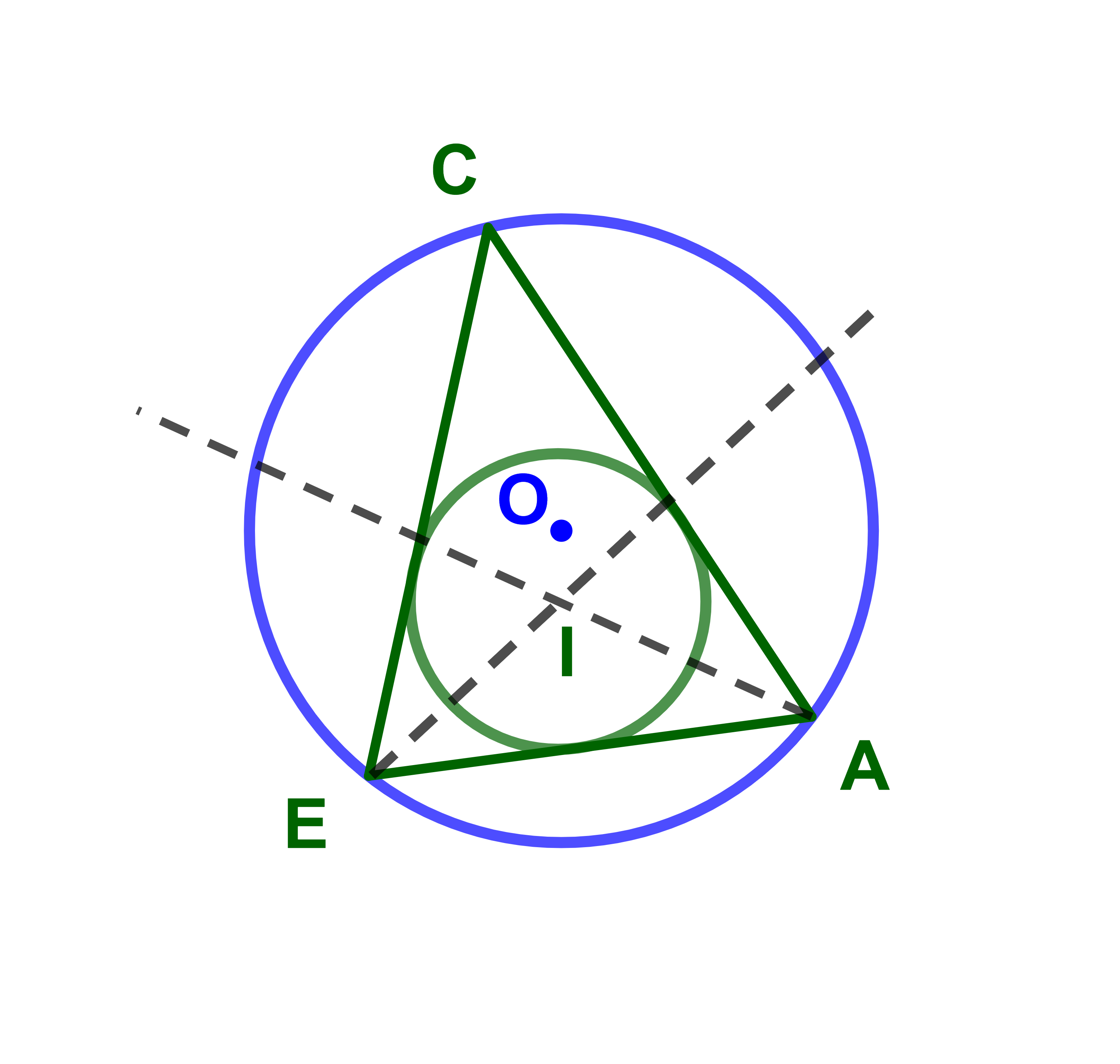
Soient (EAC) un triangle ; r le rayon du cercle inscrit dans le triangle (EAC) et R le rayon du cercle circonscrit au triangle (EAC). On pose EA=c; EC=a; AC=e. On a

a	=	e	=	c	=	2R
sin(Â)		sin(Ê)		sin(Ĉ)

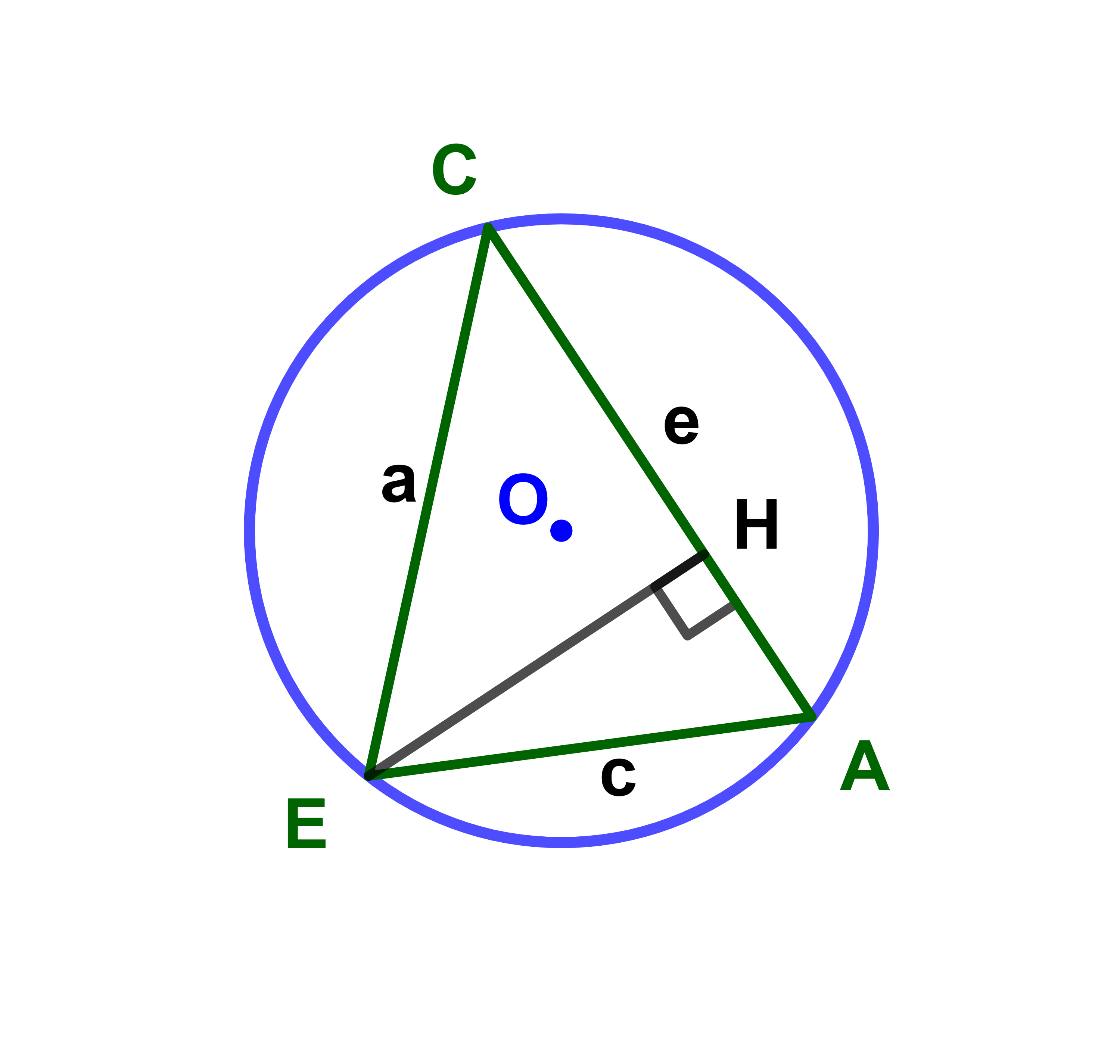
Démonstration
1) Soit H le projeté orthogonal de E sur (BC)
Les triangles AHE et HCE sont rectangles en H donc

sin =	HE	et	sinĈ =	HE
	c			a

donc c.sin Â=a.sinĈ
ou encore

a	=	b
sinÂ		sinĈ

De la même façon on montre

a	=	e
sinÂ		sinÊ

ainsi

a	=	e	=	c
sinÂ		sinÊ		sinĈ

2) On considère le trangle isocèle OEC
on sait que (OE;OC)=2(AE;AC)
donc

(EA;EO) =	π	-Ā
	2

on a

cos(EA;EO) =	a/2
	R

Donc

sinĀ =	a
	2R

ainsi

2R =	a
	sinĀ

5.2 Surface d'un triangle

5.2.1 Propriété 1

La surface du triangle EAC est définie par

S =	1	acsinÊ
	2

tels que EA=c; EC=a et AC=e.

5.2.2 Propriété 2

Soient EAC un triangle de perimètre p et r le rayon du cercle inscrit au triangle.
La surface du triangle EAC est définie par S=pr.