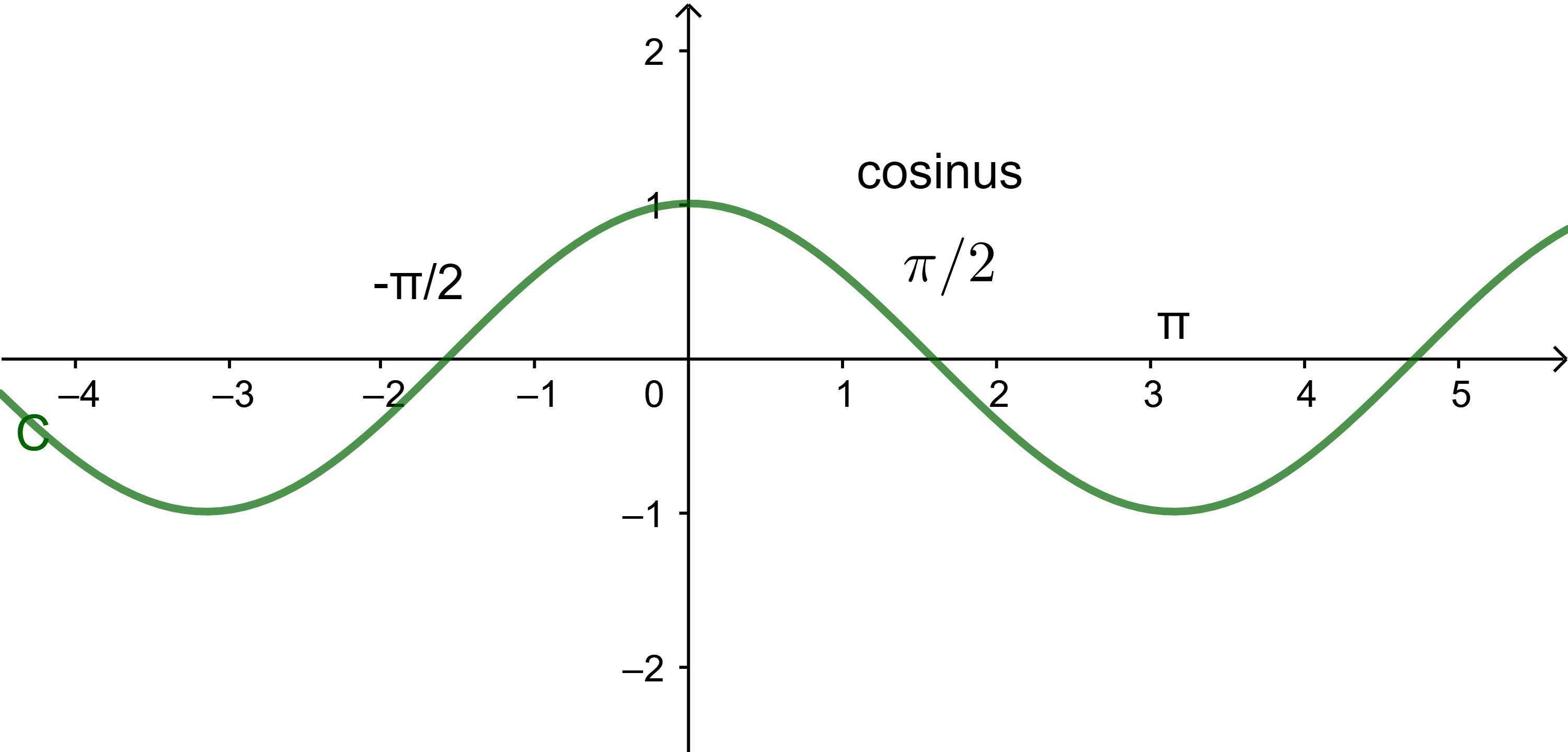
1- للتمثيل المبياني لكل من الدالتين cos و sin

1.1 الدالة جيب التمام cosinus

المستوى منسوبا الى معلم متعامد ممنظم (O;i^→;j^→).
1) الدالة cos معرفة على IR.
2) لكل x∈IR لدينا (-x)∈IR
و cos(-x)=cosx
نقول اذن ان الدالة cos زوجية.

منحنى الدالة cos مماثل بالنسبة لمحور الأراتيب.

بالاضافة الى ذلك لكل (x∈IR)
لدينا x+2π∈IR و x-2π∈IR.
ليكن x∈IR لدينا cos(x+2π)=cosx.
نقول اذن أن الدالة cos دورية دورها 2π
في هذه الحالة أجزاء منحنى جيب التمام هي نفسها على مجالات من السعة 2π.

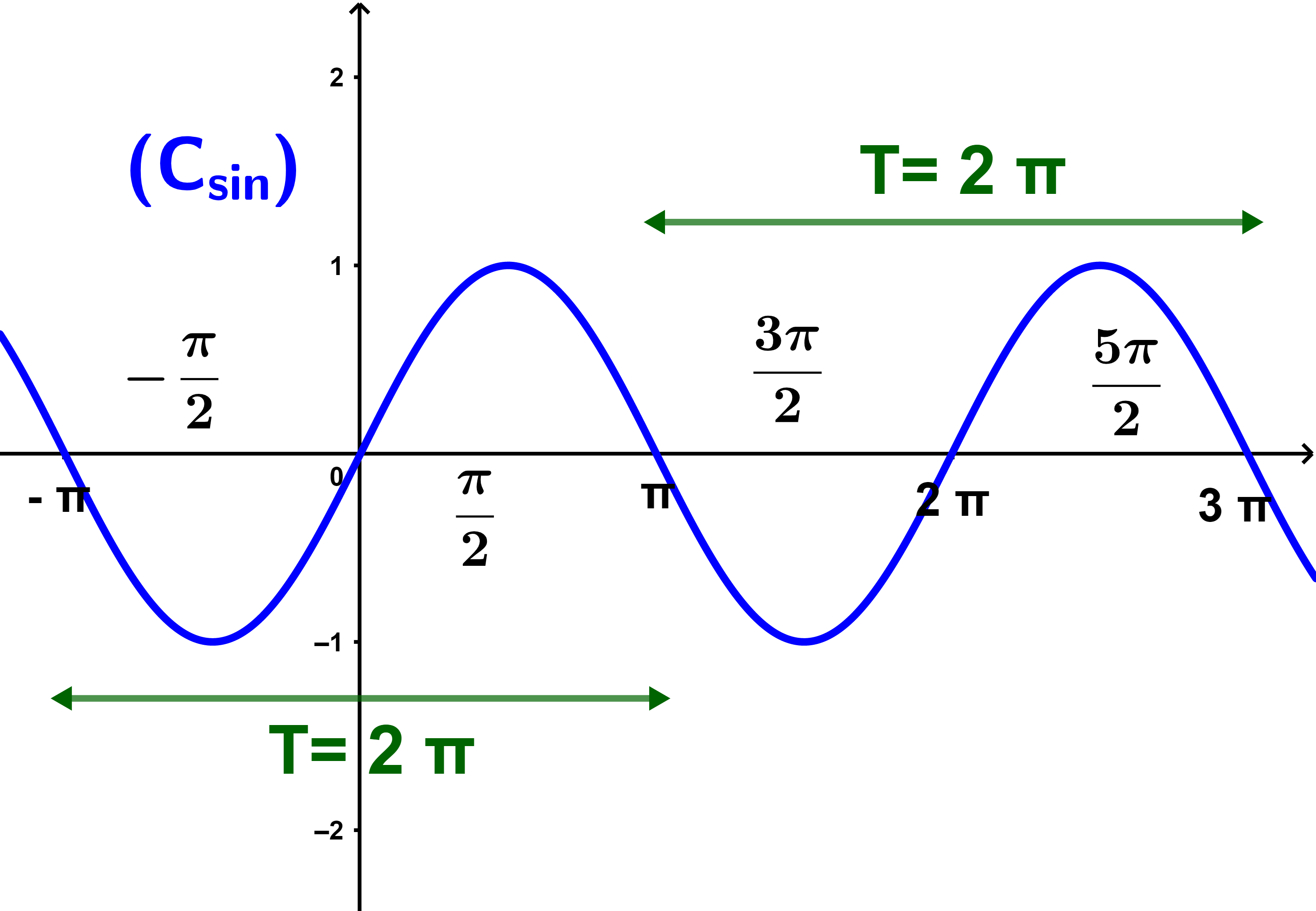
1.2 دالة الجيب sinus

المستوى منسوبا الى معلم متعامد ممنظم (O;i^→;j^→).
1) الدالة sin معرفة على IR.
2) لكل x∈IR لدينا (-x)∈IR
و sinx(-x)= -sinx
نقول اذن ان الدالة sin فردية.
منحنى الدالة sin مماثل بالنسبة لأصل المعل.

بالاضافة الى ذلك لكل (x∈IR)
لدينا x+2π و x-2π∈IR.

ليكن x∈IR لدينا sin(x+2π)=sinx.
نقول اذن أن الدالة sin دورية دورها 2π
في هذه الحالة أجزاء منحنى الجيب هي نفسها على مجالات من السعة 2π.

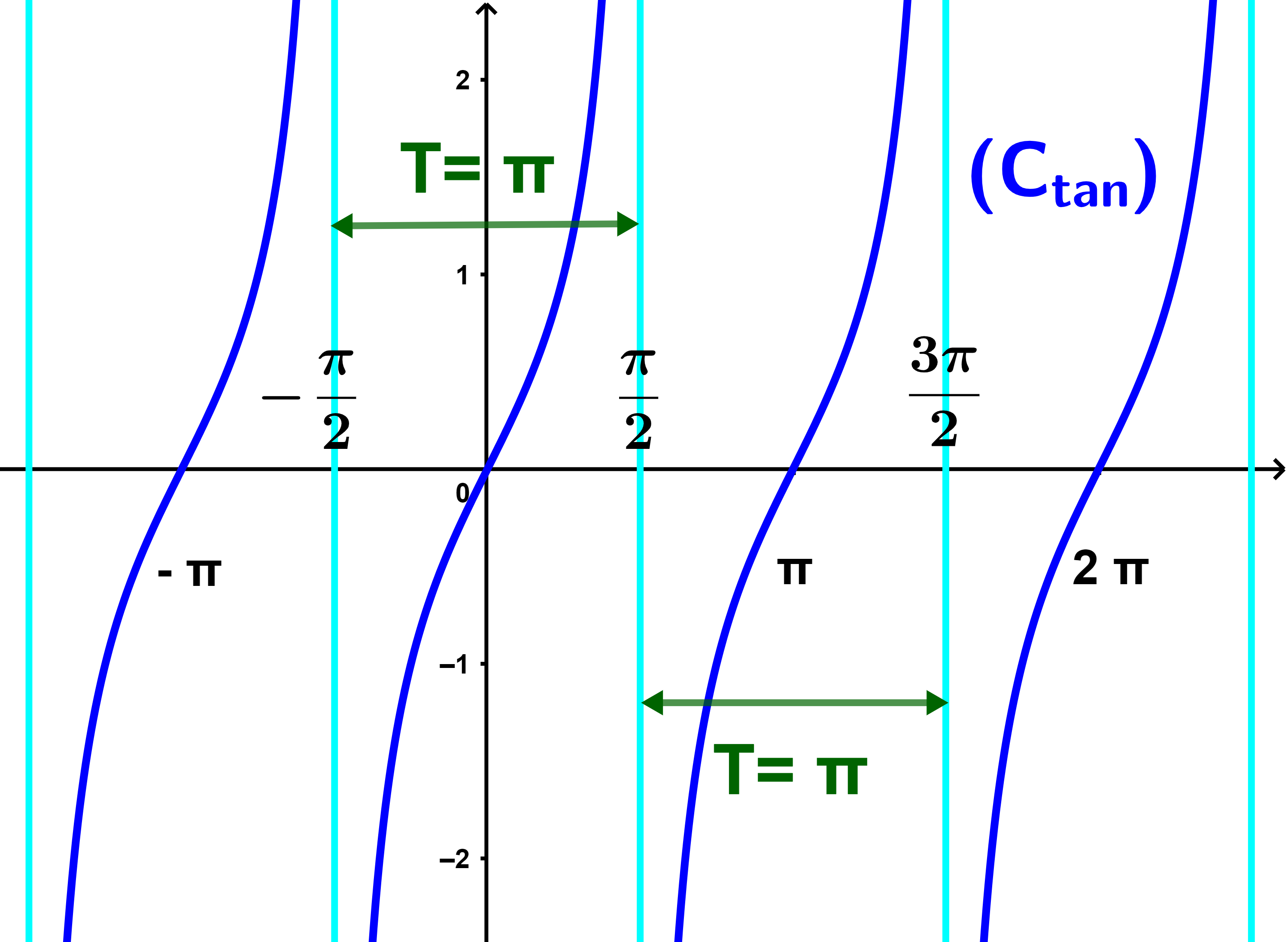
1.3 دالة الظل tangente

المستوى منسوبا الى معلم متعامد ممنظم (O;i^→;j^→).
1) الدالة tan معرفة على

D = IR \ {	π	+kπ (k∈ℤ)
	2

2) الحيز D ممركز في 0 اذن لكل (x∈D) لدينا (-x)∈D و tan(-x)=-tanx.
نقول ان الدالة tan فردية.

بالاضافة الى ذلك x∈D لدينا x+π∈D و x-π∈D.
ليكن x∈D لدينا tan(x+π)=tanx.
نقول اذن أن الدالة tan دورية دورها π
في هذه الحالة أجزاء منحنى الظل هي نفسها على مجالات من السعة π.