الحساب المثلثي (2_2)
2- المعادلات المثلثية الأساسية
2.1 تذكير
ليكن x و y عددين حقيقيين.
1) x≡y[2π] يعني يوحد عدد k∈ℤ
بحيث x=y+2kπ أي (x-y=2kπ).
مثال
| -7π | ≡ | π | [2π] |
| 4 | 4 |
لأن
| -7π | - | π | = 2x(-1)π |
| 4 | 4 |
يوجد k=-1∈ℤ.
2) x≡y[π] يعني يوجد عدد k∈ℤ
بحيث x=y+kπ أي (x-y=kπ).
مثال
| 22π | ≡ | π | [π] |
| 3 | 3 |
لأن
| 22π | - | π | = 7π |
| 3 | 3 |
يوجد k=7∈ℤ.
| x | 0 | π | π | π | π | ||||||||
| 6 | 4 | 3 | 2 | ||||||||||
| sinx | 0 | 1 | √2 | √3 | 1 | ||||||||
| 2 | 2 | 2 | |||||||||||
| cosx | 1 | √3 | √2 | 1 | 0 | ||||||||
| 2 | 2 | 2 | |||||||||||
| tanx | 0 | √3 | 1 | √3 | × | ||||||||
| 3 | |||||||||||||
2.2 المعادلة sinx = a
2.2.1 Cas particuliers
1) اذا كان a=0.
sinx=sin0=sinπ=0 يعني x=0+2kπ أو x=π+2kπ.
اذن sinx=0 يعني x=kπ بحيث k∈ℤ.
2) اذا كان a=1 فان sinx=1 يعني
| sinx = sin | π |
| 2 |
| k∈ℤ حيث x = | π | + 2kπ يعني |
| 2 |
3) اذا كان a=-1 فان sinx=-1
| sin x = sin | - π | يعني |
| 2 |
يعني
| k∈ℤ بحيث x = | - π | + 2kπ |
| 2 |
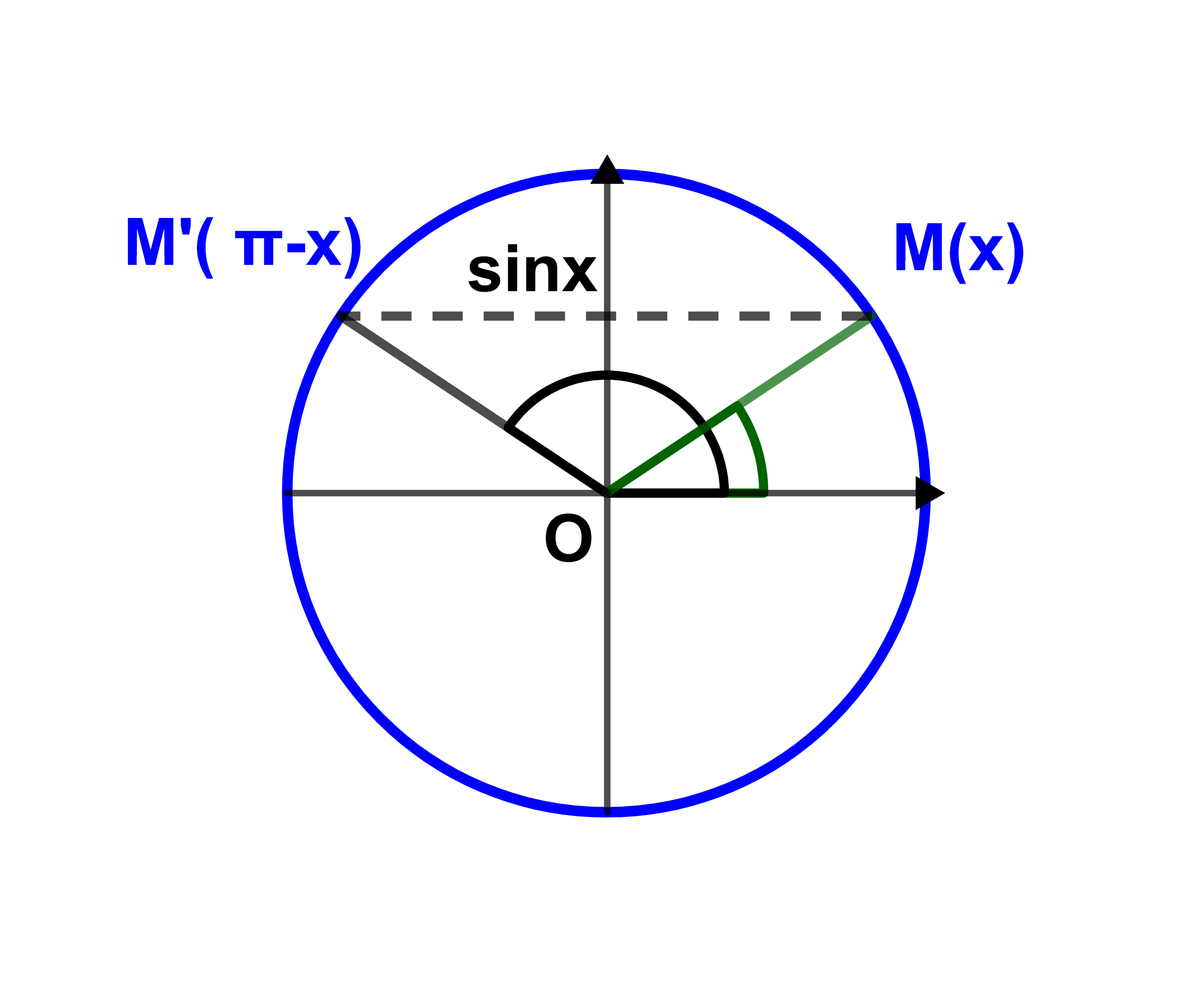
4) اذا كان a∈]-1;1[ فانه يوجد y∈IR
بحيث a=siny=sin(π-y)
اذن
sinx=a يعني x=y+2kπ أو x=π-y+2k'π
بحيث k∈ℤ و k'∈ℤ.
2.2.2 خاصية
ليكن x∈IR و a∈IR.
نعتبر المعادلة (E): sinx=a و S مجموعة حلولها في IR.
1) اذا كان a>1 أو a<-1 فان المعادلة (E) ليس لها حل.
2) اذا كان -1≤a≤1 فانه يوجد عدد y بحيث sin(y)=a بالاضافة الى ذلك
(x=y+2kπ) أو (x=π-y+2kπ) بحيث k∈ℤ و k'∈ℤ.
S={y+2kπ;π-y+2k'π/k∈ℤ و k'∈ℤ و siny=a}.