1- Représentation graphique des fonctions cos et sin

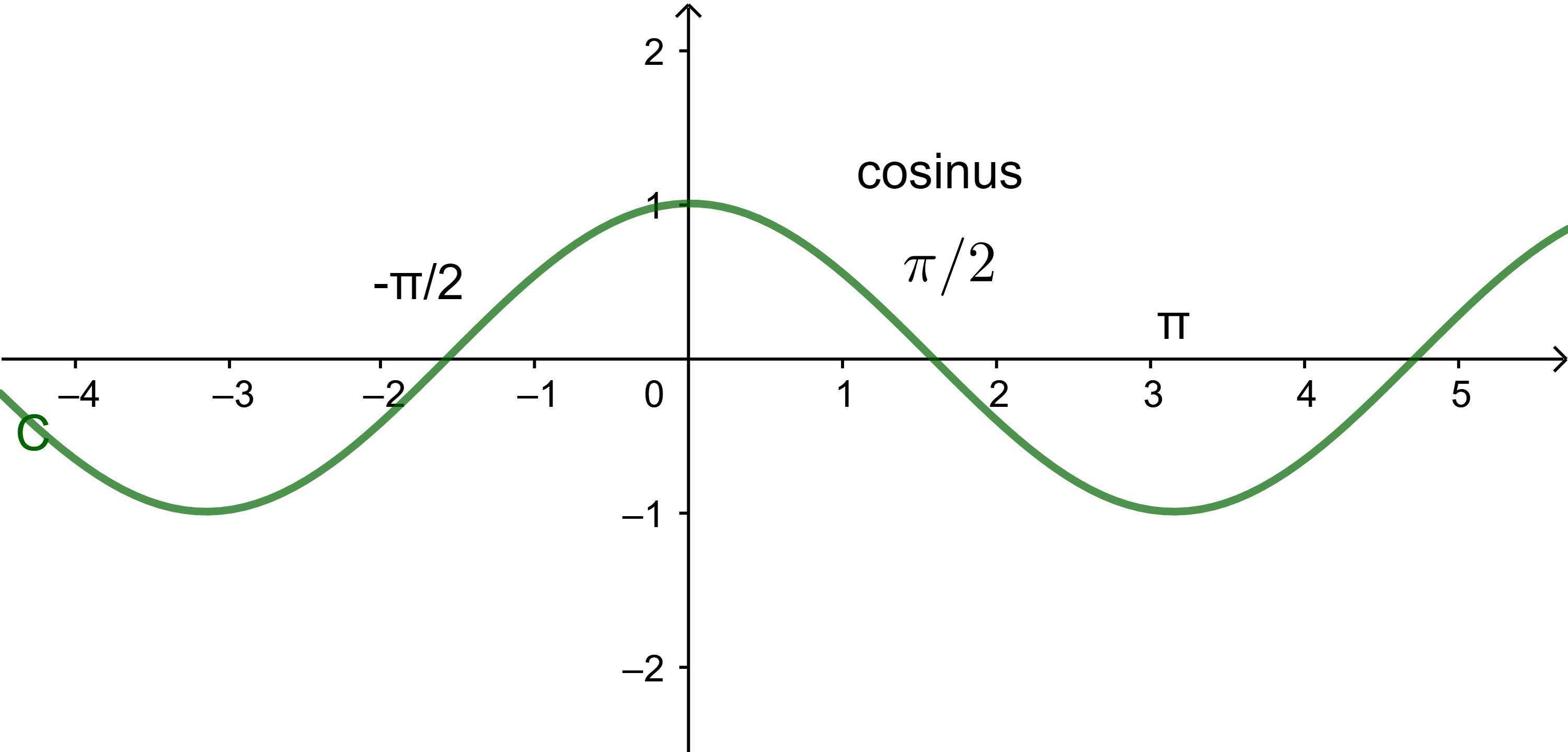
1.1 Fonction cosinus

Le plan est rapporté à un repère orthonormés (O;i^→;j^→).
1) La fonction cos est définie sur IR
2) Pour tout x∈IR on a (-x)∈IR
et cos(-x) = cosx
on dit donc la fonction cos est paire.

Ainsi la courbe représentative de la fonction cos est symétrique par rapport à l'axe des abscisses.
Et de plus pour tout (x∈IR)
on a x+2π et x-2π∈IR.
Soit x∈IR on a cos(x+2π)=cosx.
On dit donc la fonction cos est périodique de période 2π
dans ce cas les portions de la courbe cos sont les mêmes sur des intervalles d'amplitude 2π.

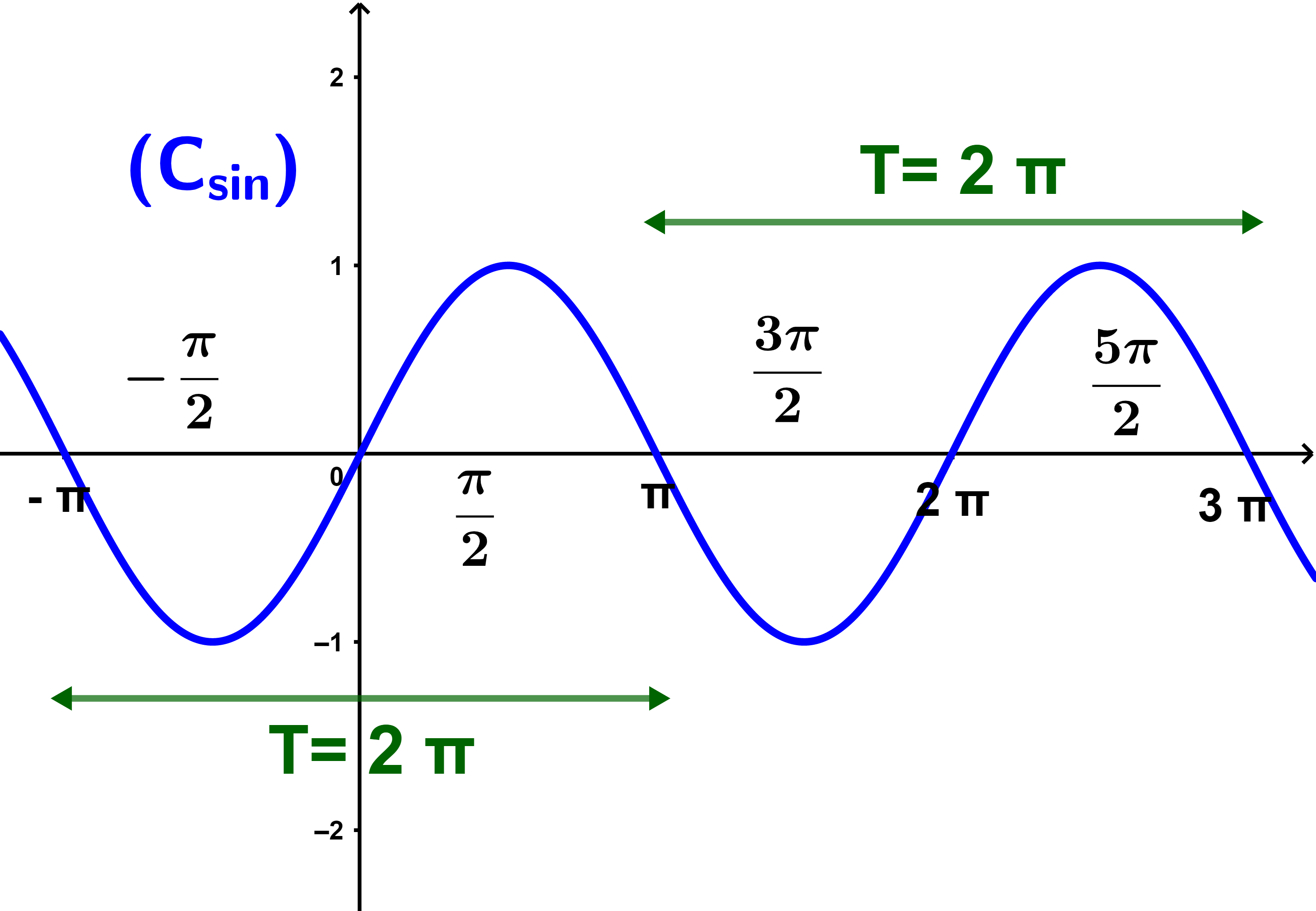
1.2 Fonction sinnus

Le plan est rapporté à un repère orthonormés (O;i^→;j^→).
1) La fonction sin est définie sur IR.
2) Pour tout x∈IR on a (-x)∈IR
et sin(-x)=- sinx.
On dit donc la fonction sin est impaire.
Ainsi la courbe représentative de la fonction sin est symétrique par rapport à O.
Et de plus pour tout (x∈IR) on a sin(x+2π)=sinx

On dit donc la fonction sin est périodique de période 2π
dans ce cas les portions de la courbe sin sont les mêmes sur des intervalles d'amplitude 2π.

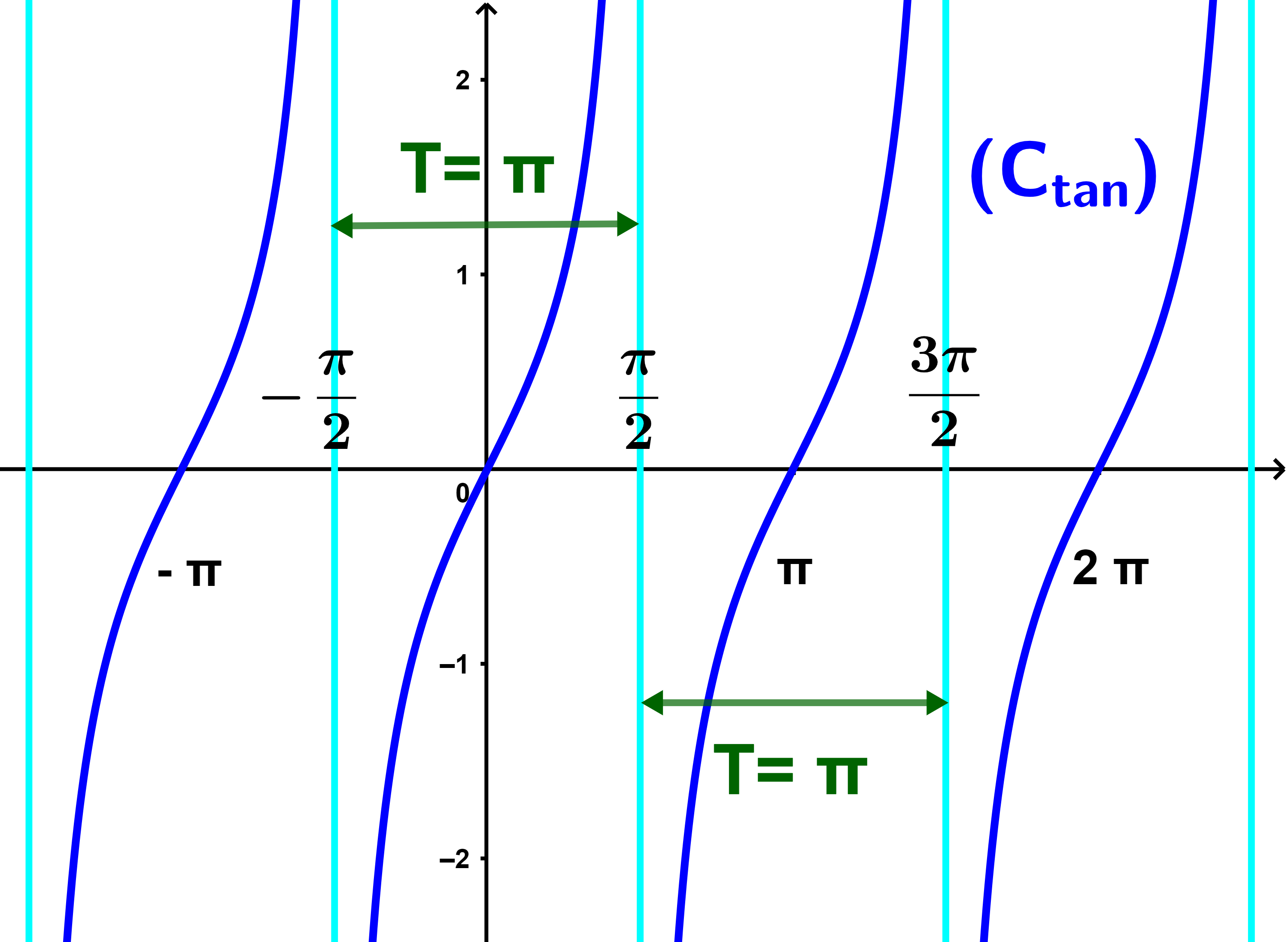
1.3 Fonction tangente

Le plan est rapporté à un repère orthonormés (O;i^→;j^→).
1) La fonction tan est définie sur

D = IR \ {	π	+kπ (k∈ℤ)
	2

2) Le domaine D est centré en 0 donc pour tout (x∈D) on a (-x)∈D et tan(-x)=-tanx.
On dit donc que la fonction tan est impaire.

Et de plus pour tout x∈D on a x+π∈D et x-π∈D Soit x∈D on a tan(x+π)=tanx.
On dit donc que la fonction tan est périodique de période π
dans ce cas les portions de la courbe tan sont les mêmes sur des intervalles ouverts d'amplitude π.