Trigonométrie (2_2)
2- Les équations trigonométriques fondamentales
2.1 Rappel
Soient x et y deux nombres réels.
1) x≡y[2π] signifie qu'il existe k∈ℤ
tel que x=y+2kπ (ou x-y=2kπ).
Exemple
| -7π | ≡ | π | [2π] |
| 4 | 4 |
Parce que
| -7π | - | π | = 2x(-1)π |
| 4 | 4 |
il existe k=-1∈ℤ.
2) x≡y[π] signifie qu'il existe k∈ℤ
tel que x=y+kπ (ou x-y=kπ).
Exemple
| 22π | ≡ | π | [π] |
| 3 | 3 |
parce que
| 22π | - | π | = 7π |
| 3 | 3 |
il existe k=7∈ℤ.
| x | 0 | π | π | π | π | ||||||||
| 6 | 4 | 3 | 2 | ||||||||||
| sinx | 0 | 1 | √2 | √3 | 1 | ||||||||
| 2 | 2 | 2 | |||||||||||
| cosx | 1 | √3 | √2 | 1 | 0 | ||||||||
| 2 | 2 | 2 | |||||||||||
| tanx | 0 | √3 | 1 | √3 | × | ||||||||
| 3 | |||||||||||||
2.2 L'équation sinx = a
2.2.1 Cas particuliers
1) Si a=0 alors
sinx=sin0=sinπ=0 signifie (x=0+2kπ ou x=π+2kπ).
donc sinx=0 signifie x=kπ tel que k∈ℤ.
2) Si a=1 alors sinx=1 signifie
| sin x = sin | π |
| 2 |
| signifie x = | π | + 2kπ tel que k∈ℤ |
| 2 |
3) Si a=-1 alors sinx=-1 signifie
| sinx = sin | - π |
| 2 |
signifie
| x = | - π | + 2kπ tel que k∈ℤ |
| 2 |
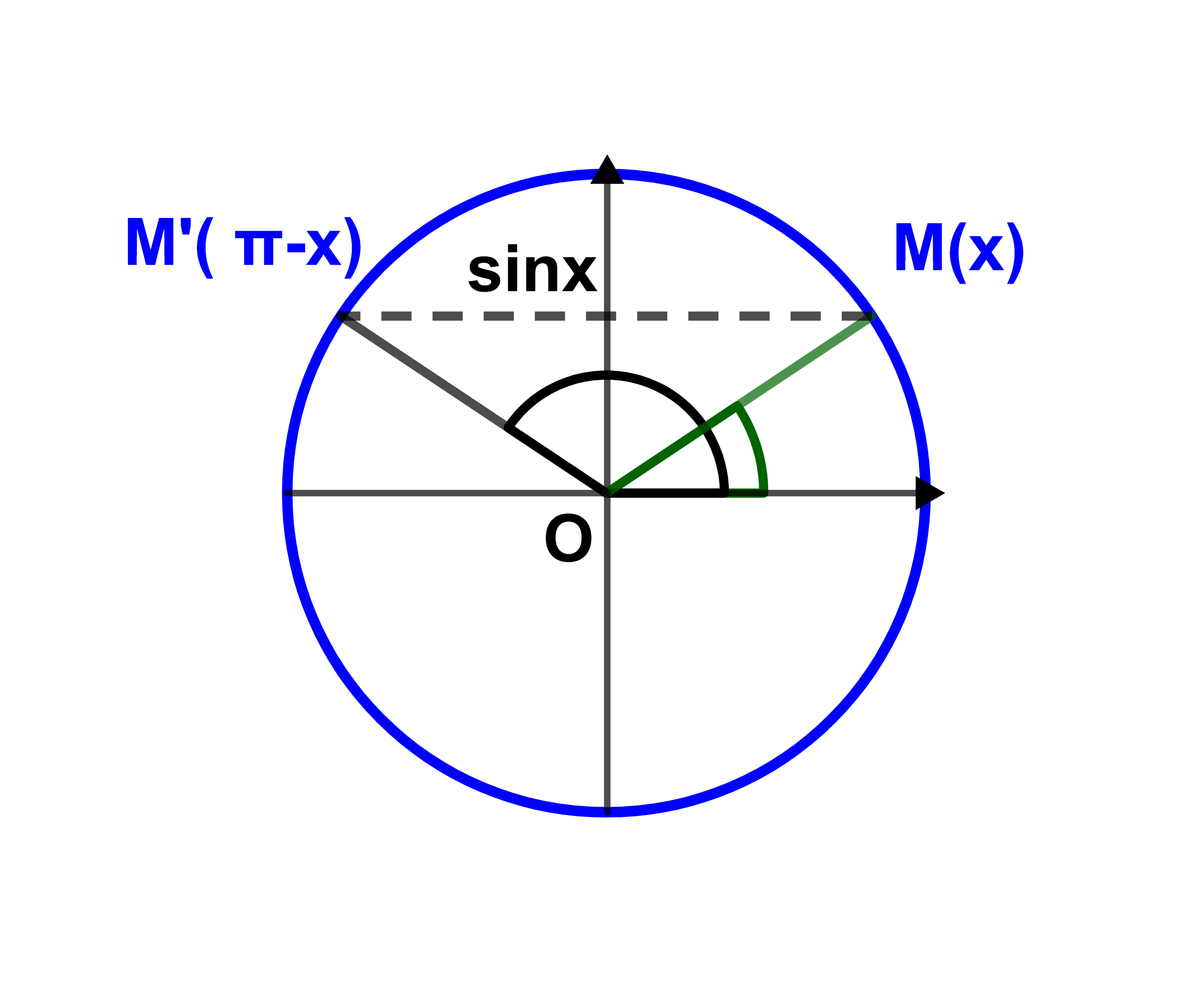
4) Si a∈]-1;1[ alors il existe y∈IR
tel que a=siny=sin(π-y)
donc
sinx=a signifie (x=y+2kπ ou x=π-y+2k'π) tel que k et k'∈ℤ.
2.2.2 Propriété
Soient x∈IR et a∈IR.
On considère l'équation (E): sinx=a et S son ensemble des solutions dans IR.
1) Si a>1 ou a<-1 l'équation (E) n'a pas de solution.
2) Si -1≤a≤1 il existe un réel y tel que sin(y)=a et de plus
(x=y+2kπ) ou (x=π-y+2kπ) tel que k et k'∈ℤ.
S={y+2kπ;π-y+2k'π/k et k'∈ℤ et siny=a}.